Hello everyone, I hope you can enjoy this special round for Zepto Lab. Here are the solutions of this round.
A. King of Thieves
This task is easy for many of you. We can just iterate over all possible i1 and i2 - i1, then we can compute i3, ..., 5, and check whether this subsequence satisfies the condition mentioned in the task.
B. Om Nom and Dark Park
We use greedy and recursion to solve this task. For each tree rooted at v, we adjust its two subtrees at first, using recursion. Then we increase one edge from v's child to v.
C. Om Nom and Candies
If there is a kind of candy which weighs greater than 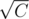 , then we can iterate over the number of it to buy, which is less than
, then we can iterate over the number of it to buy, which is less than 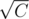 .
.
Otherwise, without loss of generality we suppose 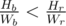 . If the number of the blue candies that Om Nom eats is more than Wr, he could eat Wb red candies instead of Wr blue candies, because Hb × Wr < Wb × Hr. It means the number of the blue candies will be less than
. If the number of the blue candies that Om Nom eats is more than Wr, he could eat Wb red candies instead of Wr blue candies, because Hb × Wr < Wb × Hr. It means the number of the blue candies will be less than 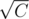 , and we can iterate over this number.
, and we can iterate over this number.
D. Om Nom and Necklace
This task is to determine whether a string is in the form of ABABA... ABA for each prefixes of a given string S
For a prefix P, let's split it into some blocks, just like P = SSSS... SSSST, which T is a prefix of S. Obviously, if we use KMP algorithm, we can do it in linear time, and the length of S will be minimal. There are only two cases : T = S, T ≠ S.
- T = S. When T = S, P = SSS... S. Assume that S appears R times. Consider "ABABAB....ABABA", the last A must be a suffix of P, and it must be like SS... S, so A will be like SS... SS, and so will B. By greedy algorithm, the length of A will be minimal, so it will be SSS... S, where S appears
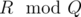 times. And B will be SSS... S, where S appears
times. And B will be SSS... S, where S appears 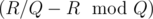 times. So we just need to check whether
times. So we just need to check whether 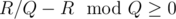 .
. - T ≠ S . When T ≠ S, the strategy is similar to T = S. A will be like "SS...ST", and its length will be minimal. At last we just need to check whether
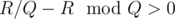 .
.
The total time complexity is O(n).
E. Transmitting Levels
Our task is to compute at least how many number of blocks are needed to partition a circular sequence into blocks whose sum is less than K.
By monotonicity, it is easy to get the length of maximal blocks which starts from 1 to n in O(n). Assume the block with minimal length is A and its length is T, it is obvious that whatever the blocks are, there must be a block that it starts in A. So, we can iterate over all the T numbers of A, making it the start of a block, and calculate the number of blocks.
Notice that all the lengths of blocks is (non-strictly) greater than T, therefore the number of blocks we need is at most N / T + 1. We need to iterate T times, but each time we can get the answer in O(N / T), so finally we can check whether the answer is legal in T * O(N / T) = O(N).
F. Pudding Monsters
Actually this problem is to compute how many segments in a permutation forms a permutation of successive integers.
We use divide and conquer to solve this problem.
If we want to compute the answer for an interval [1, n], we divide this interval into two smaller ones [1, m], [m + 1, n] where 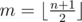 . We only care about the segments which crosses m. We call the first interval L and the latter one R.
. We only care about the segments which crosses m. We call the first interval L and the latter one R.
Considering the positiions of maximum numbers and minimum numbers in these valid segments, There are four possible cases:
- the maximum number is in L, the the minimum is also in L;
- the maximum number is in R, the the minimum is also in R;
- the maximum number is in L, the the minimum is in R;
- the maximum number is in R, the the minimum is in L;
Let A be the given sequence and we define Lmaxp = maxp ≤ i ≤ mAi. Similarly we can define Rmaxp, Rminp, Lminp.
For simplicity we only cares about case 1 and case 4.
In Case 1, we iterate over the start position of the segment, so we know the maximum and minimum number so we can compute the length of the segment and check the corresponding segment using Rmin and Rmax.
In Case 4, we iterate over the start position again, denoted as x. Suppose the right end is y, then we know that Lminx < Rminy, Lmaxx < Rmaxy so we can limit y into some range. Another constraint for y is that Rmaxy - Lminx = y - x, i.e. Rmaxy - y = Lminx - x. Note that when x varies, the valid range for y also varies, but the range is monotone, so we can maintain how many times a number appears in linear time.
It's easy to show that this algorithm runs for  , by Master Theorem.
, by Master Theorem.
There are some other people using segment trees. You can see a nice implement here
G. Spiders Evil Plan
In this task, we are given a tree and many queries. In each query, we are supposed to calculate the maximum total length of y paths with the constraint that x must be covered.
Consider S is the union of the paths (it contains nodes and edges).
For each query (x, y), if y > 1 , then there is always a method that S is connected.
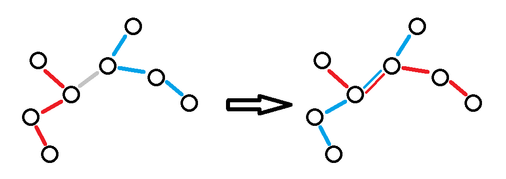
Further, we could get the following theorem:
For an unrooted tree, if it has 2k leaves, then k paths can cover this tree completely.
Proof for this theorem is that, if some edge u - v is not covered, we can interchange two paths, i.e. we change two paths a - b and c - d to a - c and b - d, for a - b in the subtree of u and c - d in the subtree of v.
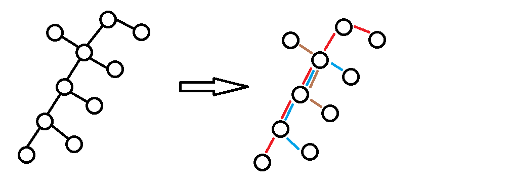
So a query (x, y) could be described as :
Find 2y leaves in the tree, with node x in S, and maximize the total of weight of the edges in S.
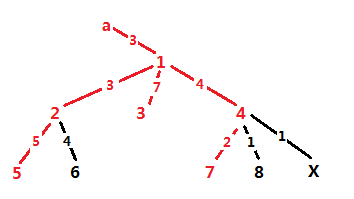
For a query (x, y), we can make x the root. Then this task is how to choose the leaves. Note that we could select leaves one by one, every time we select the leaf which makes answer larger without selecting the others, as follow :
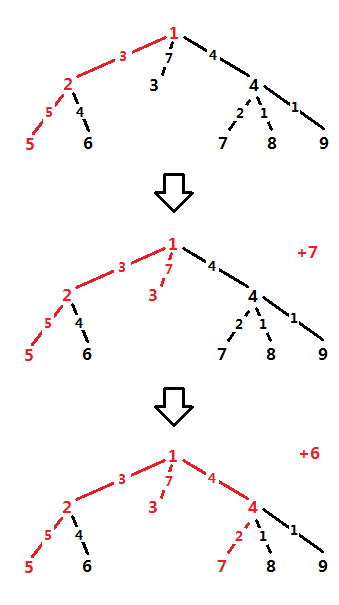
But if for every query we need to change the root, the time complexity cannot be accepted. Assuming the longest path in the tree is (a, b) , we could find that whatever the query is, S will contain either a or b certainly.
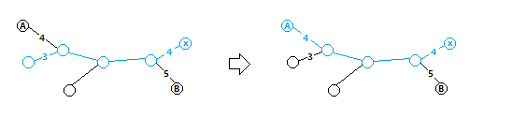
So, we just need to make a and b the root in turn, and get the maximum answers. However, there is another problem : x may not be in S. Like this :
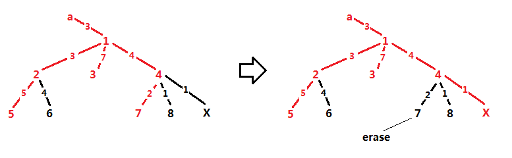
But it doesn't matter. We just need to link x with the selected, and erase some leaf. Of course after erasing, the answer should be maximum.
Thanks, for all of your excellent performance!








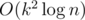 running time. The time limit is 5s in order to save Java's life. If you do some optimization, the solution can be Accepted. You can see
running time. The time limit is 5s in order to save Java's life. If you do some optimization, the solution can be Accepted. You can see  , and the complexity of Query is
, and the complexity of Query is 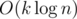 . It can pass all the test data easily but it has a really large constant. This is
. It can pass all the test data easily but it has a really large constant. This is 

