Hello, CodeForces!
From time to time some people ask questions related to center, radius and diameter of graph (I could google only about tree). In this topic you can find their definitions and algorithms for finding them.
Problem: you are given graph G = (V, E), where V is set of nodes and E is set of edges. You have to find its center, radius and diameter.
Let's denote di, j as shortest distance between nodes 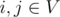 . Then diameter of graph is denoted as the greatest possible among all possible shortest distances between two nodes:
. Then diameter of graph is denoted as the greatest possible among all possible shortest distances between two nodes:
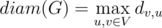
Also we can define eccentricity of node as maximal distance from that node to other:
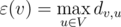
Having values of eccentricity of all nodes, we can define radius of graph as minimal one among them:
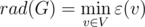
Also we can observe that diameter of graph is maximal eccentricity of node:
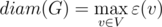
Center of graph is set of nodes with eccentricity equal to the radius of graph:
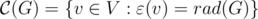
After these basic definitions we can find radius, diameter and center of graph using Floyd-Warshall's algorithm:
const int N = ...; // Number of nodes in graph
const int INF = ...; // Infinity
int d[N][N]; // Distances between nodes
int e[N]; // Eccentricity of nodes
set <int> c; // Center of graph
int rad = INF; // Radius of graph
int diam; // Diamater of graph
// Floyd-Warshall's algorithm
for (int k = 0; k < N; k++) {
for (int j = 0; j < N; j++) {
for (int i = 0; i < N; i++) {
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
// Counting values of eccentricity
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
e[i] = max(e[i], d[i][j]);
}
}
for (int i = 0; i < n; i++) {
rad = min(rad, e[i]);
diam = max(diam, e[i]);
}
for (int i = 0; i < n; i++) {
if (e[i] == rad) {
c.insert(i);
}
}
Now let's try to change problem statement: suppose that G is a tree. There is one interesting fact about trees: number of nodes in the center of tree is equal to one or two.
Possible algorithm for finding center of tree is the following: using BFS from any node (denote it as v1) find the farthest from v1 node (denote as v2), then run BFS from v2, choose the farthest node from v2 (call it v3). Nodes in the middle of the path between v2 and v3 are center of graph, distance between them is diameter. Radius of graph is half of diameter rounded up: (diam(G) + 1) / 2. I will not provide implementation of that algorithm because it look quiet bulky. Instead, I will show another algorithm which is much easier to implement.
Theorem: Let L be set of leaves of G. If |V| ≤ 2 then L is center of G, otherwice center of graph remains the same after removing of L:
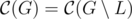
This theorem brings us to the following algorithm: remove leaves, level by level, until there are ≤ 2 nodes. These nodes will be center of graph. Implementation of this algorithm is similar to BFS:
const int N = ...; // Number of nodes in graph
int maxlevel = 0; // Level of center of graph
int level[N]; // Level of node
int degree[N]; // Degree of node
int g[N][N]; // Adjacency matrix
set <int> c; // Center of graph
queue <int> q; // Queue for algo
// Start from leaves
for (int i = 0; i < N; i++) {
if (degree[i] == 1) {
q.push(i);
}
}
while (!q.empty()) {
int v = q.front();
q.pop();
// Remove leaf and try to add its parent
for (int i = 0; i < N; i++) {
if (g[v][i]) {
degree[i]--;
if (degree[i] == 1) {
q.push(i);
level[i] = level[v] + 1;
maxlevel = max(maxlevel, level[i]);
}
}
}
}
for (int i = 0; i < N; i++) {
if (level[i] == maxlevel) {
c.insert(i);
}
}
It's not so hard to prove that after running of this algo center of graph will be in c, 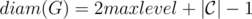 и rad(G) = (diam(G) + 1) / 2.
и rad(G) = (diam(G) + 1) / 2.
I could not fin appropriate problems to solve, feel free to post them in comments.
Problems to solve:
- IOI2013 Dreaming
- 456E - Civilization
- 592D - Super M
- Problem F from this contest
Thank you for attention, you can write about typos to private messages.











Great post, here are some problems to solve:
Dreaming IOI 2013 Day 1
Civilization
Some problems related to this acticle:
322E — Ciel the Commander
592D — Super M
Added them into post.
322E - Ciel the Commander seems to be not about center of a tree, but about centroid of a tree (proof)
Sorry, that was my mistake.
http://codeforces.com/gym/100279/attachments/download/2025/20122013-international-open-olympiad-kpiopen-2013-round-1-en.pdf Problem F here
Thank you, added to the post.
Isn't it NP-Complete to find graph diameter in random graphs? Since you'd have to solve the longest path problem.
Nope — diameter is longest among all shortest paths (Graph Diameter).
Oh, my bad. The post said :
" Let's denote d(i, j) as distance between nodes i,j. Then diameter of graph is denoted as the greatest possible distance between two nodes. "
I didn't understand it meant shortest paths.
I'll fix that.
I can prove that this algo is correct in acyclic graph.
But, will this algo working in cyclic graph?
If you are talking about finding everything using Floyd-Warshall's algorithm it should be correct for any graph.
The second algorithm works only for trees. Citation:
Now let's try to change problem statement: suppose that G is a tree.I was talking about second algorithm.
Oh, I didn't notice that sentence >< Thanks for replying.
Does the center algorithm work when the tree edges have weight?
TLE'16 December Contest — Christmas Tree Building Another problem related to this article