protypuns's blog

IOI 2015 — Boxes with Souvenirs
By protypuns, history, 9 years ago, In English

Hello guys :)

Today I tried to solve IOI 2015's first problem (Boxes with Souvenirs). I thought of dynamic programming:

dp[i] = min(dp[j] + min(l, 2 * (l - pos[j + 1]), 2 * pos[i]) ( j >= i — k and j < i)

So this algo is O(N^2) and it time limit. My question is how to reduce it to O(N).

Thanks in advance :)

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +10 Vote: I do not like it

You can make use of the fact that there will be atmost one full circle in the optimal solution.

If there is more than one full-circle then we have given 2K souvenirs ( atmost ) and spent 2L seconds.
Now say X of these souvenirs lie on the left semicircle and Y of these souvenirs lie on the right semicircle. ( X + Y = 2K )
Observe that we could have gone clockwise(for X items) or anticlockwise(for Y items) and returned without completing a full circle for each case such that the sum of time taken would have been < 2L
( This is because we take L seconds atmost for one side and L-2 seconds for the other)

Now try to construct two DPs : one for clockwise and the other for anti-clockwise.

Let DP_CW[i] = Time taken to give first 'i' teams their souvenirs moving in a clockwise direction.
DP_CW[i] = DP_CW[i-K] + ( 2 * P[i] ) , if i >= K
DP_CW[i] = 2*P[i] , otherwise.

Similarly build DP_ACW[i] for anti-clockwise direction.

You can then merge these two DPs together considering the two cases separately . ( No Full Circle and One Full Circle )

This would work in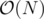 time.

Code : Boxes with Souvenirs

→ Reply