The problem has been prepared by adedalic.
To solve this problem one should remove all leading and trailing zeroes from array and then calculate the number of ones and number of zeroes neighboured by ones. The sum of this values is the answer for the problem.
Complexity: O(n).
The problem has been prepared by Oleg_Smirnov.
Let's call some path ith if we start it by going i times left, then we cross the prospect and go left n - 1 - i times again. Let di be equal to the time we should wait on traffic lights while following i-th path. If we consider any way from the shop to home, it is equal (but reversed) to only path from home to the shop, meaning that we need to find two distinct paths from home to the shop. So the answer to the problem is the sum of the smallest and the second smallest values among di. One could easily calculate di using calculated di - 1, so di could be found in one for cycle.
If we will consider only two minimum values among di, solution complexity will be O(n).
Complexity: O(n).
The problem has been prepared by Neon.
Let's store for each child his current confidence value and a boolean indicating whether child had left the queue (or visited the dentist office) or not. Then one could easily process children one by one, considering only children who still are in the queue (using boolean array), and changing stored values.
Such solution has complexity O(n2) and requires author's attention much, especially the case with possible confidence value overflowing. Of course there are much faster solutions not required in our case.
The problem has been prepared by IlyaLos.
One could consider a graph with vertices corresponding to every (x, y) position. I should notice that train positions for each Phillip position are fully restorable from his y coordinate. Edge between vertices u and v means that we could get from position corresponding to u to position corresponding by v in one turn without moving onto a train cell or moving in a cell which will be occupied by some train before the next turn. All we need next is to find whether any finishing position is reachable from the only starting position (using BFS or DFS, or, as soon as graph is a DAG, dynamic programming).
As soon as graph has O(n) vertices and O(n) edges, solution complexity equals to O(n).
585C - Alice, Bob, Oranges and Apples
The problem has been prepared by Edvard.
Firstly, let's understand the process described in problem statement. If one would write a tree of a sum-pairs (x, y) with letters 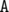 and
and  , he would get the Stern–Brocot tree. Let the number of oranges be enumerator and the number of apples be denumerator of fraction. At every step we have two fractions (at first step they are
, he would get the Stern–Brocot tree. Let the number of oranges be enumerator and the number of apples be denumerator of fraction. At every step we have two fractions (at first step they are 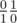 ) and should replace exactly one of them with their mediant. In such way first fraction is first parent to the left from mediant while second fraction is parent to the right. The process described in statement is, this way, a process of finding a fraction in the Stern-Brocot tree, finishing when the current mediant is equal to current node in the tree and (x, y) pair is the fraction we are searching.
) and should replace exactly one of them with their mediant. In such way first fraction is first parent to the left from mediant while second fraction is parent to the right. The process described in statement is, this way, a process of finding a fraction in the Stern-Brocot tree, finishing when the current mediant is equal to current node in the tree and (x, y) pair is the fraction we are searching.
This means that if 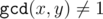 , (x, y) does not correspond to any correct fraction and the answer is "Impossible". Other way, we could find it in the tree. If x > y, we should firstly go in the right subtree. Moreover, we could then consider we are searching
, (x, y) does not correspond to any correct fraction and the answer is "Impossible". Other way, we could find it in the tree. If x > y, we should firstly go in the right subtree. Moreover, we could then consider we are searching 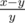 from the root. If x < y, we should go left and next consider
from the root. If x < y, we should go left and next consider 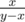 from the root. This gives us Euclidian algorithm, which could be realized to work in
from the root. This gives us Euclidian algorithm, which could be realized to work in  complexity.
complexity.
Complexity: O(logn).
The problem has been prepared by danilka.pro.
To solve the problem we will use meet-in-the-middle approach. For 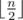 we should consider all
we should consider all 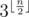 variants. Let in some variant approval values of three companions are a, b, c respectively. If we will consider some variant from other half (there are
variants. Let in some variant approval values of three companions are a, b, c respectively. If we will consider some variant from other half (there are 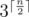 of them) and a', b', c' approval values, then to ``merge'' such two parts correctly, two conditions a - b = b' - a' и b - c = c' - b' must be true (a + a' = b + b' = c + c' is true), and the value we are maximizing is a + a'.
of them) and a', b', c' approval values, then to ``merge'' such two parts correctly, two conditions a - b = b' - a' и b - c = c' - b' must be true (a + a' = b + b' = c + c' is true), and the value we are maximizing is a + a'.
This way, to solve the task one could consider every variant from the first half and store for every possible pair (a - b, b - c) the maximum a value achievable (using, for example, the 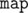 structure or any fast sorting algorithm). If one would then consider every variant from the second half, he just need to find (b' - a', c' - b') pair in the structure to get the maximum a value if possible and update answer with a + a' value. Answer restoring is pretty same to the algorithm above.
structure or any fast sorting algorithm). If one would then consider every variant from the second half, he just need to find (b' - a', c' - b') pair in the structure to get the maximum a value if possible and update answer with a + a' value. Answer restoring is pretty same to the algorithm above.
Such solution has 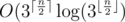 complexity.
complexity.
585E - Present for Vitalik the Philatelist
The problem has been prepared by gridnevvvit.
Let's calculate the number of subsets with gcd equal to 1 — value A. Let's do that using principle of inclusions-exclusions: firstly we say that all subsets is good. The total number of subsets is equal to 2n. Now let's subtract subsets with gcd divisible by 2. The number of that subsets is equal to 2cnt2 - 1 (cnti is the number of numbers that is divisable by i). Next we should subtract 2cnt3 - 1. Subsets with gcd divisible by 4 we already counted with number two. Next we should subtract 2cnt5 - 1. Now we should notice that subsets with gcd divisible by 6 we already processed twice: firstly with number 2, then with — 3, so let's add the number of these subsets 2cnt6 - 1. If we continue this process we will get, that for all numbers d we should add the value μ(d)(2cntd - 1), where μ(d) is equals to 0, if d is divisible by square of some prime, 1, if the number of primes in factorization of d is even and - 1 in other case. So the numbers that is divisible by square of some prime we can ignore, because they have coefficient 0. To calculate values cnti we should factorize all numbers and iterate over 2k divisors with value μ(d) ≠ 0. Now it's easy to see, that the number of subsets with gcd greater than 1 equals to B = 2n - A. To solve the problem let's fix the stamp that Vitaliy will buy ai. Let's recalculate the number B for array a without element ai. To do that we should only subtract those terms that was affected by number ai. We can do that in 2k, where k is the number of primes in factorization of the number ai. It's easy to see that only the subsets with gcd greater than 1, but not divisible by any divisor of ai, should we counted in answer. To calculate number of those subsets let's again use the principle of inclusions-exclusions. For every divisor d of ai let's subtract the value μ (2cntd - 1) from B. So now we got Bi — the number of subsets with gcd greater than 1, but coprime with ai. The answer to problem is the sum over all Bi. The maximum number of primes in factorization of number not greater than 107 is equal to 8. We can factorize all numbers from 1 to n in linear time by algorithm for finding the smallest divisors for all intergers from 1 to n, or by sieve of Eratosthenes in O(nloglogn) time.
Complexity: O(C + n2K), where 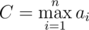 , K — is the largest number of primes in factorization of ai.
, K — is the largest number of primes in factorization of ai.
The problem has been prepared by Edvard.
Consider all substrings of string s with length 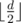 . Let's add them all to trie data structure, calculate failure links and build automata by digits. We can do that in linear time using Aho-Korasik algorithm. Now to solve the problem we should calculate dp zi, v, b1, b2, b. State of dp is described by five numbers: i — number of digits, that we already put to our number, v — in which vertex of trie we are, b1 — equals to one if the prefix that we built is equals to prefix of x, b2 — equals to one if the prefix that we built is equals to prefix of y, b — equals to one if we already have some substring with length
. Let's add them all to trie data structure, calculate failure links and build automata by digits. We can do that in linear time using Aho-Korasik algorithm. Now to solve the problem we should calculate dp zi, v, b1, b2, b. State of dp is described by five numbers: i — number of digits, that we already put to our number, v — in which vertex of trie we are, b1 — equals to one if the prefix that we built is equals to prefix of x, b2 — equals to one if the prefix that we built is equals to prefix of y, b — equals to one if we already have some substring with length 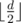 on the prexif that we built. The value of dp is the number of ways to built prefix with the given set of properties. To update dp we should iterate over the digit that we want to add to prefix, check that we still is in segment [x, y], go from vertex v to the next vertex in automata. So the answer is the sum by all v, b1, b2 zb, v, v1, v2, 1.
on the prexif that we built. The value of dp is the number of ways to built prefix with the given set of properties. To update dp we should iterate over the digit that we want to add to prefix, check that we still is in segment [x, y], go from vertex v to the next vertex in automata. So the answer is the sum by all v, b1, b2 zb, v, v1, v2, 1.
Complexity: O(nd2).











how can i get its english translation?
English translation will be ready soon.
Why is this 13576829 submission fails? I use 64-bit type here, so no overflow should occur. But is does...
13580842 AC
Oh, thank you! But... What is going on?! You've changed only the sizes of arrays, but they were large enough in both submissions.
Actually, the problem with your code was that you used scanf("%d") to read 64-bit integers, while the correct would be scanf("%I64d"). See 13584480 versus 13584478.
I can't say exactly why changing the array size from 4 × 103 to 5 × 103 made your solution pass, though. Maybe it just caused the array to be allocated in a place that was filled with zeros.
Your explanation is right, I found I used
%dto readlong long, but still got AC 13584293 ,seems interesting. Also 13584688 got WA32. I think it is because I defined the three arrays as global variables."If x > y, we should firstly go in the right subtree. Moreover, we could then consider we are searching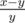 from the root. If x < y, we should go left and next consider
from the root. If x < y, we should go left and next consider 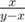 from the root."
from the root."
Could you explain the intuition behind this? I have a hard time seeing how this fits in the the Stern-Brocot tree.
Me too. I am still not able to figure out why it fits into Sterm-Brocot tree. It fits as the editorial says but I have no Idea what is the intuition behind it! Why should it fit into that form ? English translation is so poor that I have to guess meaning of every line :( Not a single line is English sentence !
I could figure it out partly as:
Let x/y be x number of apples drawn out, and y number of oranges drawn out from the bag. Now, say you have drawn out x/y and are at some branch of the tree, What happens when a card draws out? All the x/y get transferred to the other person. And some more apples and oranges are drawn out from the bag. How do we get this number?
It can be seen from the stern brocot tree that the new number is the median — (x+x1)/(y+y2) of it's parent, and the one in it's region.
I don't get the intuition either... but I will share what I managed to grasp until this point (although I can't fully say I understand everything I will mention in this post)
From what is said in the editorial, "If x > y, we should go to the right subtree," it seems that when the fraction x/y is greater then 1 then the answer always lies in the right subtree. Then, "Moreover, we could consider we are searching for (x-y)/y from the root" seems to suggest that we can now put ourselves at the new root without caring how we got here, and just search for (x-y)/y — which importantly (?) is exactly 1 less than x/y.
I will give an example of why this works, although I don't know exactly the reason behind it yet. Draw out the Stern-Brocot tree for about 5 levels including the root 1/1, and now let's look for fraction 7/4. 7 > 4, so we go to the right subtree and look for (7-4)/4 = 3/4. At this point, note that we came from the node 1/1 (looking for 7/4) and we are now on node 2/1 (looking for node 3/4). Now, note that 3/4 and 7/4 are in the same position relative to nodes 1/1 and 2/1, respectively...
Now let's look at the case where x < y. Let's look for 2/5. From node 1/1, we next go to node 1/2 and look for 2/(5-2) = 2/3. Similar to the case where x > y, 2/3 and 2/5 are in the same position relative to nodes 1/1 and 1/2, respectively!
The observation above indeed proves that the algorithm is correct, but I have yet to understand why it is works...
Hope someone can explain why it is works...
Do you know there is a book called 《Concrete Mathematics》 ? In this book, you can turn to page 121, and you will get what you want in details :)
"root" means root of the whole tree.
Possible I can answer this quistion
Let's make a 2*2 matrix
((a,a'),(b,b'))
a means the first person's apple
b mean's the first person's orange
Let's think about the operation B ((a,a'),(b,b')) * ((1,0),(1,1)) = ((a+a',a'),(b+b',b')) so we make B=((1,0),(1,1))
Let's think about the operation A ((a,a'),(b,b')) * ((1,1),(0,1)) = ((a,a+a'),(b,b+b'))
so we make A=((1,1),(0,1))
Let's define a function f:
f((a,b),(a',b'))=(b+b')/(a+a')
then we can find that:
if S is a statement ((a,a'),(b,b'))
then f(B*S)=(a+a' + b+b')/(a+a')=f(S)+1
so if f(B*s)=m/n f(s)=(m-n)/n if f(A*s)=m/n f(s)=m/(n-m)
so if (n>m) we can know the first step is A and then we need to find m/(n-m) if (m>n)we can know the first step is B and then we need to find (m-n)/m
i'm sorry for that i don't know how to write math formula in the codeforces... i'm sorry for my poor English..
Let A(x, y) = (x, y + x) and B(x, y) = (x + y, y). Note that A and B are linear transforms, meaning that A(a, b) + A(c, d) = A((a, b) + (c, d)) and likewise for B. Additionally, let (x, y)sum = x + y.
We are trying to find a function M (composition of As and Bs) such that M(1, 0)sum = x and M(0, 1)sum = y. Call (x, y) reachable if such a function M exists. Let x > y without loss of generality. We are trying to prove that (x, y) is reachable if and only if (x - y, y) is reachable. We will only prove the forward case here. The backwards case follows a similar argument.
Statement (forward case): If (x, y) is reachable, then (x - y, y) is reachable.
Proof: If (x, y) is reachable, then by definition there exists a function M such that M(1, 0)sum = x and M(0, 1)sum = y. Note that the since x > y, the inner-most function of M must be an A. There then exists an L such that M = L(A()). Note that L(0, 1)sum = L(A(0, 1))sum = M(0, 1)sum = y and L(1, 0)sum = L(A(1, 0) - (0, 1))sum = L(A(0, 1))sum - L(0, 1)sum = M(1, 0)sum - L(0, 1)sum = x - y. Hence, (x - y, y) is reachable through L.
Can anyone explain me how to solve Div2 Problem D in detail?
Suppose that trains are fixed and the person do moves as follows: 1. Move right 2. Move up or move down or don't move 3. Move right 4. Move right
Then, you can solve this problem with DP. You can see my code. http://codeforces.com/contest/586/submission/13563032
hi:) first ty for The contest,i got Wrong Answer in Problem C(Div 2),i really dont know why!:( can any one help me??:( ( my algorithm is O(n) ) http://codeforces.com/contest/586/submission/13590330
Consider this input:
Your answer is 1 2 4 and it should be 1 2. First kid scare off third one and there are two remaining, one goes in and scare the other. Your solution tries to compute everything in one go, but every time you need to compute decreasing scream first and then do the runnning. Hence O(n^2) complexity. Hope this helps.
Got it:) Thank you so much...
the time limit for Div.1 D seems a little strict. There are many accepted solutions with time >=1500ms , and many who failed because they exceed the TL by a small amount, even though they used the same algorithm as the editorial.
Yes, it is, I spent ~20 mins optimizing my solution ._.
If you use "map" twice, you will get TL. Just use it once, you can AC.
Hi, does anyone know if there is another solution for "585C — Alice, Bob, Oranges and Apples" (div1 C) ? Do I have a method to solve it if I don't know Stern-Brocot tree ? Thanks!
My teammate danilka.pro solved it without knowing about Stern-Brocot tree.
Slightly weak tests on div 1 D:
Some solutions that sort the resulting values will not find the maximum answer correctly, and some solutions using a map will overwrite previous values in a map keyed by pairs of differences. Most such solutions fail on this test:
where the only correct solution is to take all the 1's. For example this practice solution of mine which is clearly wrong due to this passes: 13576496. For an example contest submission that fails, see 13565708. (thus it's not a small bug specific to my implementation)
Also BTW my purpose in making these posts is to let others know their solution may not be correct. I'm not blaming anyone; I know this kind of thing inevitably happens. My goal in solving problems is not to get AC, but to have a correct solution, and I will try to fix any AC solution if it isn't completely right. I try to help others with similar goals.
Thank you for test-case. It was added to upsolving.
Wow, I didn't know you could do that. Thanks!
In problem Div2/D can any one explain why these are the possibles moves :
s R R R
or
s R U R R
or
s R D R R
( U=Up R=Right D=Down )
13563714
from the problem statement, the valid moves are R,RU,RD , then the trains will move two steps to the left, which is equal to the person moving two steps to the right, so RRR,RURR,RDRR
I got it thanks :)
For Div 1 E:
Should be μ(d)(2cntd - 1) instead.
Fixed thanks. Missed μ(d) when translating to English.
Does anybody solve 585A on Python? I guess it's impossible to pass test 32 using Python as programming language
Status > Verdict:Accepted + Language:Python2/3 > Nobody solved, but some solutions are with PyPy2/3. Python and other scripting languages are to slow for these constraints?
I have solved it simply resend my solution with pypy 2.5 instead of python 2
13652262 2015-10-15 22:52:35 shade33 C — Стоматолог Геннадий PyPy 2 Полное решение 296 мс 8200 КБ 13651833 2015-10-15 22:44:33 shade33 C — Стоматолог Геннадий Python 2 Превышено ограничение времени на тесте 32 1000 мс 900 КБ
How about now? Does anybody solve 585A on Python? I also think it is almost impossible.
I haved passed 72 tests. I don't know how to pass more.
Can you help me?
Solved Div1 F using Suffix Automaton. I think it's a nice problem for Suffix Automaton. This process don't need any pre-processing of d/2 length substrings. Nice problem in deed :)
The memory limits for div1 E are strict for solution given in editorial. How do you keep 8 factors of 107 numbers, that will be 8 * 107 which is around 320MB and can't be kept in 256MB limit. I could not use vectors as well. Can you provide code?
We can also view problem C Div 1 geometrically like this:
First, we have two vectors A(1, 0) and B(0, 1) and our target is vector C(x, y)
To reach target C, we can do two operations, either transform A = A + B, or B = A + B. We are done when A + B = C
if x == y, we cannot have a solution.
if x != y, we notice that, the angle (A, C) and (B,C) are always in opposite directions. Which means, in clockwise order, we have vector A -> C -> B. So, our task becoming, transform vector A into A + max*B with max is the maximum number that maintain order A -> C -> B, max can easily be found using binary search.
My submission
Thanks buddy.! This one was the best solution and was quite logical. I couldn't have solved this one if you didn't comment this. Solution
Problem Gennady the Dentist was good experience for me to think about O(n) idea.
In Div2D testcase 6, there is a train of length 1.
585A . Gennady the Dentist ... Of course there are much faster solutions not required in our case.
How we can do better ? It seems we have to simulate every thing and I can't find any solution! Am I wrong ?