Немного отойду от традиции и создам немного неоффтопную тему. Наверняка, здесь есть много спортивных программистов,которые интересуются теорией чисел и теорией сложности.
Специально для них (и для всех остальных желающих) хочу предложить следующую задачу:
Пускай есть циклическая группа 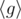 порядка q. Существуют два алгоритма: первый из них это некий Algo1, который работает следующим образом:
порядка q. Существуют два алгоритма: первый из них это некий Algo1, который работает следующим образом: 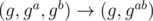 , 1 ≤ a, b ≤ q. Сторонним наблюдателям, таким как мы с вами, неизвестны ни a, ни b, ни g, ни q. Просто они формально есть, и мы знаем, что алгоритм работает таким образом.
, 1 ≤ a, b ≤ q. Сторонним наблюдателям, таким как мы с вами, неизвестны ни a, ни b, ни g, ни q. Просто они формально есть, и мы знаем, что алгоритм работает таким образом.
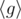 порядка q. Существуют два алгоритма: первый из них это некий Algo1, который работает следующим образом:
порядка q. Существуют два алгоритма: первый из них это некий Algo1, который работает следующим образом: 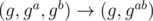 , 1 ≤ a, b ≤ q. Сторонним наблюдателям, таким как мы с вами, неизвестны ни a, ни b, ни g, ни q. Просто они формально есть, и мы знаем, что алгоритм работает таким образом.
, 1 ≤ a, b ≤ q. Сторонним наблюдателям, таким как мы с вами, неизвестны ни a, ни b, ни g, ни q. Просто они формально есть, и мы знаем, что алгоритм работает таким образом.Второй из них - это некий Algo2, который работает следующим образом: 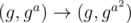 , 1 ≤ a ≤ q.
, 1 ≤ a ≤ q.
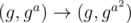 , 1 ≤ a ≤ q.
, 1 ≤ a ≤ q.Собственно вопрос: необходимо доказать их эквивалентность в смысле сложности ( ну или говоря другими словами, показать полиномиальную сводимость друг к другу).
UPD. Для некого упрощения задачи, будем считать следующее - данная группа 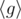 задает некоторую подгруппу мультипликативной группы поля
задает некоторую подгруппу мультипликативной группы поля 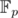 , причем ее порядок q пусть будет пока нечетным.
, причем ее порядок q пусть будет пока нечетным.
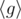 задает некоторую подгруппу мультипликативной группы поля
задает некоторую подгруппу мультипликативной группы поля 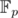 , причем ее порядок q пусть будет пока нечетным.
, причем ее порядок q пусть будет пока нечетным.Под эквивалетностью работы понимается следующее:
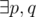 , многочлены, такие что
, многочлены, такие что 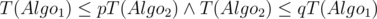 .
.










В общем, пока ответа нет, я здесь написал свои соображения.
Не знаю, правильно ли єто, но попробую:
второй алго можно свести к первому: (g, ga) -> (g, ga, ga) -> (g, ga, gb).
То есть, аналогичность очевидна. А насчёт сложности - нужно поиграть с О-символикой для простого сложения или умножения функций.
Извините, был напуган.
Хотя нет, это неверно, т.к. -g^{b/2} -- не степень g и нам не гарантируют, как отработает алгоритм корректно.