Codes in nicer format will be uploaded later.
658A - Bear and Reverse Radewoosh and 639A - Bear and Displayed Friends — codes.
639B - Bear and Forgotten Tree 3 and 639C - Bear and Polynomials — codes.
639D - Bear and Contribution — codes.
639E - Bear and Paradox — codes.
639F - Bear and Chemistry — codes.
658A - Bear and Reverse Radewoosh — Iterate once from left to right to calculate one player's score and then iterate from right to left. It's generally good not to write something similar twice because you are more likely to make mistakes. Or maybe later you will find some bug and correct it only in one place. So, try to write calculating score in a function and run them twice. Maybe you will need to reverse the given arrays in some moment.
639A - Bear and Displayed Friends — You should remember all friends displayed currently (in set or list) and when you add someone new you must check whether there are at most k people displayed. If there are k + 1 then you can iterate over them (over k + 1 people in your set/list) and find the worst one. Then — remove him. The intended complexity is O(n + q*k).
639B - Bear and Forgotten Tree 3 — You may want to write some special if for n = 2. Let's assume n ≥ 3. If d = 1 or d > 2h then there is no answer (it isn't hard to see and prove). Otherwise, let's construct a tree as follows.
We need a path of length h starting from vertex 1 and we can just build it. If d > h then we should also add an other path from vertex 1, this one with length d - h. Now we have the required height and diameter but we still maybe have too few vertices used. But what we built is one path of length d where d ≥ 2. You can choose any vertex on this path other than ends of the path (let's call him v), and add new vertices by connecting them all directly with v. You can draw it to see that you won't increase height or diameter this way. In my code I sometimes had v = 1 but sometimes (when d = h) I needed some other vertex and v = 2 was fine.
639C - Bear and Polynomials, my favorite problem in this contest. Let's count only ways to decrease one coefficient to get the required conditions (you can later multiply coefficient by - 1 and run your program again to also calculate ways to increase a coefficient).
One way of thinking is to treat the given polynomial as a number. You can find the binary representation — a sequence with 0's and 1's of length at most 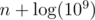 . Changing one coefficient affects up to
. Changing one coefficient affects up to 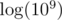 consecutive bits there and we want to get a sequence with only 0's. We may succeed only if all 1's are close to each other and otherwise we can print 0 to the output. Let's think what happens when 1's are close to each other.
consecutive bits there and we want to get a sequence with only 0's. We may succeed only if all 1's are close to each other and otherwise we can print 0 to the output. Let's think what happens when 1's are close to each other.
Let's say that we got a sequence with two 1's as follows: ...00101000.... Decreasing by 5 one coefficient (the one that was once in a place of the current first bit 1) will create a sequence of 0's only. It's not complicated to show that decreasing coefficients on the right won't do a job (because the first 1 will remain there) but you should also count some ways to change coefficients on the left. We can decrease by 10 a coefficient on the left from first 1, or decrease by 20 a coefficient even more on the left, and so on. Each time you should check whether changing the original coefficient won't exceed the given maximum allowed value k.
One other solution is to go from left to right and keep some integer value — what number should be added to the current coefficient to get sum equal to 0 on the processed prefix. Then, we should do the same from right to left. In both cases maybe in some moment we should break because it's impossible to go any further. In one case it happens when we should (equally) divide an odd number by 2, and in the other case it happens when our number becomes too big (more than 2·109) because we won't be able to make it small again anyway.
639D - Bear and Contribution — It isn't enough to sort the input array and use two pointers because it's not correct to assume that the optimal set of people will be an interval. Instead, let's run some solution five times, once for each remainder after dividing by 5 (remainders 0, 1, 2, 3, 4). For each remainder r we assume that we should move k people to some value x that 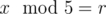 (and at the end we want at least k people to have contribution x). Note that x must be close to some number from the input because otherwise we should decrease x by 5 and for sure we would get better solution. The solution is to iterate over possible values of x from lowest to highest (remember that we fixed remainder
(and at the end we want at least k people to have contribution x). Note that x must be close to some number from the input because otherwise we should decrease x by 5 and for sure we would get better solution. The solution is to iterate over possible values of x from lowest to highest (remember that we fixed remainder 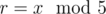 ). At the same time, we should keep people in 5 vectors/lists and do something similar to the two pointers technique. We should keep two pointers on each of 5 lists and always move the best among 5 options. The complexity should be O(n·5).
). At the same time, we should keep people in 5 vectors/lists and do something similar to the two pointers technique. We should keep two pointers on each of 5 lists and always move the best among 5 options. The complexity should be O(n·5).
639E - Bear and Paradox — It's good to know what to do with problems about optimal order. Often you can use the following trick — take some order and look at two neighbouring elements. When is it good to swap? (When does swapping them increase the score?) You should write some simple formula (high school algebra) and get some inequality. In this problem it turns out that one should sort problems by a fraction 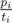 and it doesn't depend on a constant c. There may be many problems with the same value of
and it doesn't depend on a constant c. There may be many problems with the same value of 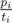 and we can order them however we want (and the question will be: if there is a paradox for at least one order). Let's call such a set of tied problems a block.
and we can order them however we want (and the question will be: if there is a paradox for at least one order). Let's call such a set of tied problems a block.
For each problem you can calculate its minimum and maximum possible number of granted points — one case is at the end of his block and the other case is to solve this problem as early as possible so at the beginning of his block. So, for fixed c for each problem we can find in linear time the best and worst possible scores (given points).
When do we get a paradox? Where we have two problems i and j that pi < pj (pi was worth less points) we solved problem i much earlier and later we got less points for problem pj. We can now use some segment tree or sort problems by pi and check whether there is a pair of problems with inequalities we are looking for — pi < pj and maxi > minj where maxi and minj we found in the previous paragraph.
We can do the binary search over the answer to get complexity 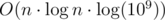 or faster. Can you solve the problem in linear time?
or faster. Can you solve the problem in linear time?
639F - Bear and Chemistry — Task is about checking if after adding some edges to graph, some given subset of vertices will be in one biconnected component. Firstly, let's calculate biconnected components in the initial graph. For every vertex in each query we will replace it with index of its bicon-component (for vertices from subset and for edges endpoints). Now we have a forest. When we have a list of interesting vertices in a new graph (bicon-components of vertices from subset or edges) we can compress an entire forest, so it will containg at most 2 times more vertices than the list (from query) and will have simillar structure to forest. To do it, we sort vertices by left-right travelsal order and take LCA of every adjacent pair on the sorted list. If you have compressed forest, then you just have to add edges and calculate biconnected components normally, in linear time.










For 639B, can you explain why v=1 won't always work?
Something like this:
If d = h and you will add something to v = 1 then you will increase diameter to d + 1.
Yeah, in my code I accounted for that, however I thought that if d=h then n-1 must equal d. I never thought of adding the extra vertices to v=2 instead of v=1 to avoid increasing the diameter if n-1 > d.
My Submission: 17001667
Another way to solve 639C - Bear and Polynomials is trivially solving equation for each a_i. The problem is, during solving equation we may have very big numbers, so let's calculate them by 10 random modules greater than 1e9. If resulting value is less then all modules, it will be the same by each modulo. Be careful with negative numbers, we can handle them by subtracting each modulo from each value. My code is here 16999208.
Even 2 primes greater than 1e9 worked. I used 1e9+7 and 1e9+9. Probability of error is pretty small (10^(-18)), even then. It's actually a much easier code as well, from the one described in the editorial.
I used 1e9+7 and 1e12+39 as modulos during contest but it gave me WA on Test 24. Changing the second modulo to 1e9+9 gives AC.
WA Submission with 1e12+39 Modulo: http://codeforces.com/contest/657/submission/17005524
AC Submission with 1e9+7 Modulo: http://codeforces.com/contest/657/submission/17009452
Any idea why?
Overflow?
but what if the resulting value is bigger? how to prove it is right by just checking the equality of
int pos = d[0]; int neg = d[0] - mods[0];I'm confused about that, and I'll be very grateful if u can explain it more specificallysilly am I. I got it...
Can you tell me why do we have to choose multiple modules? I was trying to solve this problem and was thinking the same thing but only with one modulo(1e9+7). Why is it necessary to choose multiple modules. Is it a complex maths behind it or something else?
Its been 4 months since the contest. There is a fat chance any body would reply. Even then.. :P
You calculate the answer using only one modulo m1 and get the result r. How can you be sure that it's really r, but not r+m1 or r+2m1 or r+10m1? Every m1-th number has the same remainder.
Now you use two modulos m1 and m2. You get the same result r by both (coprime) modulos. It means the real result can be r or r+m1*m2 or r+2*m1*m2, and so on. The probability of fail greatly decreases.
Then you take 10 modulos and nothing can stop you.
In E you don't really need segment tree, if you iterate from small p's to big you'll have to check maximum of all numbers that were before. But we still needed sort, so complexity is n log n log(10^6)
It seems it may be done in O(n (log n + log 10^6)) if we carefully sort in advance. Did you mean that by "linear"? I doubt that really linear solution exists because you'll at least need to sort input
You do not need to sort at every binsearch iteration (all orders, by p and by are fixed and don't depend on c, so complexity is
are fixed and don't depend on c, so complexity is 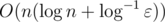 .
.
yep, I was just editing it in when you wrote it:)
lol, there was a typo in Editorial. I wrote "or solve problems by" instead of "or sort problems by". Yep, I agree that sorting is easier.
You actually don't need the binary search on c if you note that assuming problems are sorted by p, getting more points for every problem with point value pi compared to problems with point values pi - 1 means the whole sequence is correct (because all pi - 1 problems get more points than the earlier ones anyway).
You do still need the sorting, though.
In 639C — Bear and Polynomials, to deal with negative numbers, I allowed to store negative bits in representation too. But I am getting WA on test 45. What is special about it? My code outputs 0 instead of 30.
639D — Bear and Contribution : How to solve this using binary search ?
DIV2B for any value of K . CODE
nice !
How does this solution (Bear and Polynomials) work?
I think this solution basically performs Synthetic Division — another way to check if a number is a root of a polynomial.
Incorect solution got accepted in problem C: represent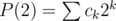 , where
, where 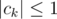 and print 0, if not all
and print 0, if not all 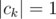 are close to each other. It fails on test a0 = 0, a1 = - 1, ..., an - 1 = - 1, an = 1
are close to each other. It fails on test a0 = 0, a1 = - 1, ..., an - 1 = - 1, an = 1
Can you show me this accepted solution? My solution with this approach got WA 45, and the mistake in case when they are not close to each other My solution itself
link
Can someone explain me what the difference in these solutions, why first works this and second this gives WA 45? The only difference is in 61-63 lines, but as I can see they should do the same thing (the same representation as a result)?
Can someone please give some more explanation for Div2 D : Bear and Polynomials ?
a+b*2^1+c*2^2+d*2^3 can be converted into a%2+(a/2+b)*2^1+c*2^2+d*2^3 . which further can be converted into a%2+((a/2+b)%2)*2^1+ ((a/2+b)/2+c)*2^2+d*2^3 and so on.... in reverse direction a+b*2^1+c*2^2+d*2^3 can be converted into a+b*2^1+(c+2*d)2^2+0*2^3 and so on. so for each i we have to convert all the multiple of 0 to i-1 and i+1 to n-1 into multiple of 2^i and check this multiple is less than equal to k or not.now the trick is if any multiple of 0 to i-1 is 1 or -1 after modules then we can not convert it into multiple of 2^i . we also have to check in reverse direction that if it's multiple is greater than 2*k then we can not go further because all the upcoming multiple's are greater than k . here is link to my solution. http://www.codeforces.com/contest/658/submission/17020224
Thanks, that was really an insightful explanation.
I like to write small insights, so if you like this one, I write a few more :)
Let's consider the polynomial: P(x) = 31 + 15x + 7x2 + 3x3 + x4
The input to the program will look like that:
4 10031 15 7 3 1Every number can be expressed using binary representation instead of base-10. So, let's see how coefficients of our polynomial will look in binary form:
P(x) = 31 + 15·x + 7·x2 + 3·x3 + 1·x4
=P(x) = 111112 + 11112·x + 1112·x2 + 112·x3 + 12·x4
Ok, now let's see what happens when we try to evaluate polynomial P(2) = P(102):
P(2) = 31 + 15·2 + 7·4 + 3·8 + 1·16
=P(102) = 111112 + 11112·102 + 1112·1002 + 112·10002 + 12·100002
The last thing I will do in this comment is align the binary numbers, so this becomes even more insightful:
a0·x0 = 111112
a1·x1 = 111102
a2·x2 = 111002
a3·x3 = 110002
a4·x4 = 100002
Probably, it is now evident that the binary representation is more thought-provoking in this problem than the usual base-10 representation :)
I am confused as to how to work with negative numbers in the problem 639C — Bear and Polynomials. Would adding negative bits for negative numbers work ? Also, if I do so I cannot tell if the required value will be within 'k'. Could somebody pls help me out.
In case P(2) < 0 you can change signs of all coefficients.
In problem F, why do you say that forest will be left after biconnected components contraction? In general, it should be a DAG and LCAs are not well-defined on it.UPD. I misread both the problem and editorial
Are you about strongly connected components?
I misread the problem and though that the graph is directed and we need to dynamically check strong connectivity ><
Graph is undirected in this problem.
In 639D - Bear and Contribution, that does "iterate over possible values of x from lowest to highest" mean? Don't we need to sort all these values first?
Yes, we should sort the input first. Then for each r we should iterate over the sorted input and check all x that:
So why the complexity is not O(n log n)?
Unfortunately, I haven't learnt how to write formulas in comments yet.
yeah, it will be . I didn't care about it because it
. I didn't care about it because it
sortis very quick and generally it doesn't change much. Sorry for confusing.Isn't the complexity of reference c++ solution provided for the problem 639D - Bear and Contribution is O(n*25).
Yes, this solution is O(n·d2) apparently.
Why C. Bear and Polynomials's second example's output is 0?How about change a3 into 0?
I get it.Thanks!
Because in a valid polynomial Q, the problem states that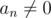 .
.
But how about this case:
3 20 1 14 -7Could I change a1 into 0 ?a0.I'm sorry.Could I change a0 into 0?
Oh,I get it!It's an not ai.
Thanks.
639F: what is this compressed forest that is being talked about? Can someone elaborate on what the "left-right" traversal order is and what we achieve by taking LCA?Edit: Damn, that is a very, very clever technique. Thanks for sharing your sample code!
I was trying to understand F with the definition of biconnected component as given for example here, but it seems the one being used in all the codes is not quite the same. For example the graph with edges (1,2), (1,2),(2,3),(2,3) would consist of only one component instead of two. Is this okay or am I getting something wrong?
Seems to me like what is being built is this: https://threads-iiith.quora.com/The-Bridge-Tree-of-a-graph