680A - Bear and Five Cards
Iterate over all pairs and triples of numbers, and for each of them check if all two/three numbers are equal. If yes then consider the sum of remaining numbers as the answer (the final answer will be the minimum of considered sums). Below you can see two ways to implement the solution.
680B - Bear and Finding Criminals
Limak can't catch a criminal only if there are two cities at the same distance and only one of them contains a criminal. You should iterate over the distance and for each distance d check if a - d and a + d are both in range [1, n] and if only one of them has ti = 1.
679A - Bear and Prime 100
If a number is composite then it's either divisible by p2 for some prime p, or divisible by two distinct primes p and q. To check the first condition, it's enough to check all possible p2 (so, numbers 4, 9, 25, 49). If at least one gives "yes" then the hidden number if composite.
If there are two distinct prime divisors p and q then both of them are at most 50 — otherwise the hidden number would be bigger than 100 (because for p ≥ 2 and q > 50 we would get p·q > 100). So, it's enough to check primes up to 50 (there are 15 of them), and check if at least two of them are divisors.
679B - Bear and Tower of Cubes
Let's find the maximum a that a3 ≤ m. Then, it's optimal to choose X that the first block will have side a or a - 1. Let's see why.
- If the first block has side a then we are left with m2 = m - first_block = m - a3.
- If the first block has side a - 1 then the initial X must be at most a3 - 1 (because otherwise we would take a block with side a), so we are left with m2 = a3 - 1 - first_block = a3 - 1 - (a - 1)3
- If the first blocks has side a - 2 then the initial X must be at most (a - 1)3 - 1, so we are left with m2 = (a - 1)3 - 1 - first_block = (a - 1)3 - 1 - (a - 2)3.
We want to first maximize the number of blocks we can get with new limit m2. Secondarily, we want to have the biggest initial X. You can analyze the described above cases and see that the first block with side (a - 2)3 must be a worse choice than (a - 1)3. It's because we start with smaller X and we are left with smaller m2. The situation for even smaller side of the first block would be even worse.
Now, you can notice that the answer will be small. From m of magnitude a3 after one block we get m2 of magnitude a2. So, from m we go to m2 / 3, which means that the answer is O(loglog(m)). The exact maximum answer turns out to be 18.
The intended solution is to use the recursion and brutally check both cases: taking a3 and taking (a - 1)3 where a is maximum that a3 ≤ m. It's so fast that you can even find a in O(m1 / 3), increasing a by one.
679C - Bear and Square Grid
Let's first find CC's (connected components) in the given grid, using DFS's.
We will consider every possible placement of a k × k square. When the placement is fixed then the answer is equal to the sum of k2 the the sum of sizes of CC's touching borders of the square (touching from outside), but for those CC's we should only count their cells that are outside of the square — not to count something twice. We will move a square, and at the same time for each CC we will keep the number of its cells outside the square.
We will used a sliding-window technique. Let's fix row of the grid — the upper row of the square. Then, we will first place the square on the left, and then we will slowly move a square to the right. As we move a square, we should iterate over cells that stop or start to belong to the square. For each such empty cell we should add or subtract 1 from the size of its CC (ids and sizes of CC's were found at the beginning).
And for each placement we consider, we should iterate over outside borders of the square (4k cells — left, up, right and down side) and sum up sizes of CC's touching our square. Be careful to not count some CC twice — you can e.g. keep an array of booleans and mark visited CC's. After checking all 4k cells you should clear an array, but you can't do it in O(number_of_all_components) because it would be too slow. You can e.g. also add visited CC's to some vector, and later in the boolean array clear only CC's from the vector (and then clear vector).
The complexity is O(n2·k).
679D - Bear and Chase
Check my code below, because it has a lot of comments.
First, in O(n3) or faster find all distances between pairs of cities.
Iterate over all g1 — the first city in which you use the BCD. Then, for iterate over all d1 — the distance you get. Now, for all cities calculate the probability that Limak will be there in the second day (details in my code below). Also, in a vector interesting let's store all cities that are at distance d1 from city g1.
Then, iterate over all g2 — the second city in which you use the BCD. For cities from interesting, we want to iterate over them and for each distinct distance from g2 to choose the biggest probability (because we will make the best guess there is).
Magic: the described approach has four loops (one in the other) but it's O(n3).
Proof is very nice and I encourage you to try to get it yourself.
679E - Bear and Bad Powers of 42
The only special thing in numbers 1, 42, ... was that there are only few such numbers (in the possible to achieve range, so up to about 1014).
Let's first solve the problem without queries "in the interval change all numbers to x". Then, we can make a tree with operations (possible with lazy propagation):
- add on the interval
- find minimum in the whole tree
In a tree for each index 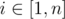 let's keep the distance to the next power of 42. After each "add on the interval" we should find the minimum and check if it's positive. If not then we should change value of the closest power of 42 for this index, and change the value in the tree. Then, we should again find the minimum in the tree, and so on. The amortized complexity is O((n + q) * log(n) * log42(values)). It can be proved that numbers won't exceed (n + q) * 1e9 * log.
let's keep the distance to the next power of 42. After each "add on the interval" we should find the minimum and check if it's positive. If not then we should change value of the closest power of 42 for this index, and change the value in the tree. Then, we should again find the minimum in the tree, and so on. The amortized complexity is O((n + q) * log(n) * log42(values)). It can be proved that numbers won't exceed (n + q) * 1e9 * log.
Now let's think about the remaining operation of changing all interval to some value. We can set only one number (the last one) to the given value, and set other values to INF. We want to guarantee that if t[i] ≠ t[i + 1] then the i-th value is correctly represented in the tree. Otherwise, it can be INF instead (or sometimes it may be correctly represented, it doesn't bother me). When we have the old query of type "add something to interval [a, b]" then if index a - 1 or index b contains INF in the tree then we should first retrieve the true value there. You can see that each operation changes O(1) values from INF to something finite. So, the amortized complexity is still O((n + q) * log(n) * log42(values).
One thing regarding implementation. In my solution there is "set < int > interesting" containing indices with INF value. I think it's easier to implemement the solution with this set.











All of the editorials have been timed just as the contest ends, but still I have to say thanks a lot for satiating our curiosity for solutions as soon as the contest finished. Thanks for a great round
P.S. Also thanks for many solutions, as sometimes it is hard to understand if there is only one per problem
That was a very fast editorial! Thank you for a fun round!
Not a big issue, but for 679B "Cubes" editorial, the second bullet point should be,
no?
Thank you, corrected.
An interesting fact: there is a formula to calculate a(n) — the smallest volume of tower consisting of n blocks:
a(n) = a(n-1) + ceil(\sqrt{a(n-1)/3+1/4}-1/2)^3 for n >= 2.
(https://oeis.org/A055402)
Yeah, OEIS is powerful. Though, I didn't see how to use this formula to solve a problem.
I don't understand the meaning of the sequence. Could you elaborate?
It answers a bit different question: What is the smallest volume of a tower, that — built with the greedy algorithm from the problem- consists of exactly n blocks?
Yes — as Errichto pointed — it's not very useful in the problem, but I wrote about is just as an interesting fact, because it was a bit surprising for me. Actually it could help only with estimating maximal number of blocks.
Alternate idea for Bear and Tower of Cubes.
First construct the minimum possible X such that you use maximum number of blocks. This can be done greedily. Store all the sides of cubes. Now we need to convert this ans to maximum. For that, loop over the sides of cubes in decreasing order. Keep increasing the side of cube till it is valid.
Code
Unfortunately during the contest I had a bug in code which I found after the contest. :(
Here it seems like you are trying to do a greedy version of a knapsack-type problem, and it doesn't feel like it should give the right answer every time. Please update us with the status of the resubmission (whether it gets AC or not). In my opinion it should not.
Later edit: It seems like it got accepted (I should see the links before commenting, shouldn't I?). But why is that?
AC on resubmit. Code
Exactly what I did.
Outline of proof of correctness:
An increasing sequece of positive integers a0, ..., an - 1 is called valid if it form blocks of some tower, which is equivalent to the condition that a03 + ... + ai3 < (ai + 1)3 for all 0 ≤ i < n. It is not hard to see that greedily adding the smallest possible ai will result in the maximum number of blocks.
Suppose that the current sequence is a0, ..., an - 1 and the optimal sequence is b0, ..., bn - 1. Since the sequence is constructed greedily, ai ≤ bi for all 0 ≤ i < n. So it is always possible to convert a to b by increasing some ai. By the validity of the sequence, a03 + ... + an - 13 < (an - 1 + 1)3. So if it is possible to increase an - 1, it is always optimal to do so. Similarly, if it is not possible to increase an - 1, it is always optimal to increase an - 2, ... and so on.
Interesting! A quick question about the second part: why can't increasing an - 3 and an - 2 yield a greater result than just increasing an - 1?
No matter how you increase an - 2, an - 3, ..., a0, you can't make the total volume ≥ (an - 1 + 1)3, whereas if you increase an - 1, the first cube alone has volume ≥ (an - 1 + 1)3.
I'm just wondering why it is always optimal to increase the largest cube?
Got TL in C because of map<int,int> instead of simple array :/ with array it's ~600ms.
Could Anybody explain me, how to get "12 941" in Div1 B when input is 994? I see that 729+216+27+8+8+1+1+1+1+1+1=941 and it's just 11...
729 + 216 + 27 + 8 + 8 + 1 + 1 + 1 + 1 + 1 + 1 = 994, not 941 as you wrote.
Ah, you're right, silly me.
@Errichato our first task in Div1B is find max no of blocks and then find maximum X. (1<=X<=M) so for m = 994, ans will be 14 798 how it is 12 941 ?
I guess for X = 798 Limak won't use 14 blocks.
Will russian version of editorial available?
There will be only English version, sorry for the inconvenience.
in problem d of div2 are we fixing a square of side k and for all k*k members we are subtracting 1 if it's part of a component which lies outside this k*k zone and then doing it for all possible rows from 0 to n-k (and k columns in that zone). Could someone plz explain the editorial (to a fool like me) in very SIMPLE terms. Thanks in advance
The slower approach is the following. For each possible placement subtract 1 from the size of a connected component which contains this cell. Then, iterate over connected components and for each of them if it touches the k × k square then add its size to some current sum (possible answer). Also, you must add k2 (size of the k × k square) to the "current sum".
To make this solution faster, you should use the technique called sliding-window (described in the editorial). Also, you can google more tutorials about this technique.
can someone please explain the problem Bear and Tower of Cubes?
Let me try to explain to you. All you need to realise is that, the answer to a given number 'm', will not be worse than a given number of 'm-1'. Why? Notice that, we don't have to construct a tower having exactly 'm' volume. The problem only requires that we build a tower with a volume less or equal to 'm'. Thus, if the answer to build a tower with exact volume of 'm-1' is better than building a tower with exact volume of 'm', we can just build the smaller tower instead.
After realising this point, you can compare those cases mentioned in the tutorial. In the first case, we have initial volume of 'm', then after selecting size 'a' block, the left volume is m — a^3. In case 2, the left volume is a^3 — (a-1)^3. We just simply choose the case which has larger remaining volume. I think code2 in the editorial has a better reflection of this idea.
Yeah you're right, it all rests on the fact that when we recurse we actually just want the bigger number, as that will always be at least as good as any number below it.
The reason not to pick (a-2) then is that if you solve the inequality
(a-1)^3 — 1 — (a-2)^3 > a^3 -1 — (a-1)^3
then you get a < 1. which means a <= 0 and we know that the smallest a = 1, so therefore this is impossible.
The reason a-1 can be better than a is because m could be equal to a^3 or a^3+1 or something like that, while for (a-1) we always have the whole range of possible numbers to choose from (a-1)^3 to a^3 — 1, and then choosing a-2 will never be better.
Why is that? It seems somewhat intuitive, but for example X=15 is better than X=16. Any ideas how would you (roughly) go about proving this?
The point is: m = 16 is not worse than m = 15. Because both allow for all X up to 15 and the former also allows for something else (X = 16).
Yeah we're recursing on m not on X.
And since we can prove that choosing an X that would make us remove a block of (a-2) can never be as good as the two above (you can also add more rigor to what I did above, like checking that the X value returned from the recursion would always be lower for the one with a-2 than the one with a-1 even if they had the same amount of blocks), then it must be sufficient to just check removing block of size a or block of size a-1
When I read D I knew that it would have a beautiful solution: glad to see the magic did not disappoint me :D
I had a different approach for problem B.
If the order is
O(v²)shouldn't it be TLE? I mean, |v| is 10⁵, right?No, as the editorial says, |v| is very small. I didn't do the exact calculatios during contest, but I assumed it would be pretty small. The editorial claims that |v| is at most 18 in the worst case, so |v|2 is blazingly fast.
Oh, I missed the part of "the added blocks". Sorry!
Is there any proof for second part? Our problem is knapsack and you do it greedily?
My code on above idea.Thanks tenshi_kanade .
link:- http://codeforces.com/contest/680/submission/18376742
Thanks for the interesting contest!
can someone explain bear and square grid using sliding window technique.PLzz!! I specifically did not understand this paragraph "We will used a sliding-window technique. Let's fix row of the grid — the upper row of the square. Then, we will first place the square on the left, and then we will slowly move a square to the right. As we move a square, we should iterate over cells that stop or start to belong to the square. For each such empty cell we should add or subtract 1 from the size of its CC (ids and sizes of CC's were found at the beginning)." in the editorial and even more specifically this part "As we move a square, we should iterate over cells that stop or start to belong to the square.". Thanks in advance(I m new to programming so plz go easy on me).
Let's fix the upper left corner at (i1, j1). Then i2 = i1 + K - 1 and j2 = j1 + K - 1. The included cells in this case are in the range (i1 - 1, j1 - 1) to (i2 + 1, j2 + 1), except cells (i1 - 1, j1 - 1), (i1 - 1, j2 + 1), (i2 + 1, j1 - 1) and (i2 + 1, j2 + 1).
To do this efficiently, let's fix i1 and initialize j1 = 1. We can then calculate it by visiting all mentioned cells, then when we move j1 to the right, we only need to remove cells in the range (i1, j1 - 2) to (i2, j1 - 2) and add cells in the range (i1, j2 + 1) to (i2, j2 + 1). Additionally, we need to remove cells (i1 - 1, j1 - 1) and (i2 + 1, j1 - 1) and add cells (i1 - 1, j2) and (i2 + 1, j2). Of course, we don't consider cells that are out of the board. Once we've reached the state with j1 = N - K + 1, we need to reset all the counters, and we can do it the same way we initialized them for j1 = 1.
So we perform K2 operations at the start of every row, and then as we move j1 to the right, we perform around 2K operations each time, so the algorithm's complexity is in the order of O(N * K2 + N2 * K) = O(N2 * K).
thanku so much i understand now
In div2 E ,How to count for current window how many of the nodes of the component are outside and how many are inside?
I have the same doubt but could you plz explain me how to select the window
According to editorial,we have to select all possible windows having size k*k there can be at max n*n such windows which will completely fit inside the grid
It's described in the editorial, and you can check my code for details. We need an array to remember for each CC how many cells are outside the square at this moment (for this square).
Got it!! Thanks.. Awesome problem btw..
I'm not really convinced why in D Div2 you should always select side a and a-1 but not a-2. The reason is that having a smaller quantity doesn't necessarily yield less towers.
Can you tell me where's my mistake?
It does necessarily yield less volume because Limak builds tower greedily.
It isn't "having a smaller quantity". It's "smaller upper limit m". I claim that for smaller m the answer is not better.
I wasn't able to prove this claim during contest. But we still have a similar solution without using this claim:
Find correct answer (both, maximum number of blocks, and corresponding maximum X) for m=(i^3-1) for all i<=100000. Say f(m) gives optimal pair for m. For finding f(m), find largest i such that i^3 <= m. You already have optimal pair for X <= (i^3-1). For X>=i^3 , Limak will always choose block i^3. Now you can find f(m-i^3) recursively.
Code
Oh, I see. This makes more sense.
I suppose that the proof given in the Errichto solution can be solved using induction but I find it very counter-intuitive, or maybe that's just me.
I didn't use induction.
There is no much to prove. Think about it this way. The best answer for m up to 100 is worse (or the same) as the best answer for m up to 200. Because "m up to 200" also considers all m up to 100.
Thank you for your patience! Now I understand! :)
Thanks for the quick editorial, I'd imagine many div2 participants would stop working after finishing Problem C, the gap between C and D is pretty huge... Perhaps the interactive question tutorial helped out most of us more than expected.
For 3rd problem my first submission got WA on pretest 5 but I can't understand why ? Can anybody help me?? Here is the submission. http://codeforces.com/contest/680/submission/18318572
In the last part, when you check if the number is divisible by (whoDivided[0])^2, or the square of prime, you did not cin>>string to get the answer. The string that you initiated has random behavior. so in most cases, that string would not be yes.
After correcting that, it gives WA on testcase 6.
Submission
EDIT --> Thanks w1n5t0n. Accepted
After checking if the number is divisible by prime^2, you should print composite if yes, and prime if no. In your code, after checking if prime^2 is in range, you assume that the answer would be composite if prime^2>100, which is wrong. If the number cant be divided by prime^2, then it would be a prime number.
In problem Div1D (Bear and Chase) on the code you say:
Why you said the probability of predicting immediately is 1 / n, instead of 1 / cnt_cities, if you already now that bear will be in a city with distance d1 from g1?
I agree with marX. Why is it not
1.0 / cnt_cities?My bad, I get it now. It's because you're getting the probability for Lamak to be one of them:
1.0 / cnt_cities, multiplied by the probability that the dist will occur:cnt_cities / n.So in total, it becomes
1.0 / cnt_cities * cnt_cities / n == 1.0 / nUnderstood, it wasn't clear to me at first, actually I was wondering why he didn't multyplied by cnt / n, but he did all of this implicitely in the code.
Hikari9 explained it correctly — we multiply two factors.
A few words from me. In probability problems it's often better to think about "how much it counts towards the answer". In other words, how much it increases the answer. If you use BCD in g1 first day then from whole omega (among all possible situations) what is the probability of winning in the situation when we get info "distance is 0" and thus we guess this city immediately?
in tower of cubes why a and a-1 are the possible options why not a-2 or less ? Although it seems to be working for smaller values but I am not able to figure it out why it will work for each case for sure ! Can anyone help ?
And this comment.
thanks YangZhao512 Errichto :) I got it .
[submission:http://codeforces.com/contest/680/submission/18336927]
I have no idea why did I fail on case 16... What did I forgot to take care of, can somebody help me please? Thanks in advance.
Edit: whoops, wrong submission link :P
Thanks for the very good contest.
My implementation of the algorithm mentioned in the editorial for Div2 D Submission
In prob E div 2 Bear And Square Grid, I didnt use any vector to store which CCs are adj to curr. k*K square.I made an 1D array of [500*500] elements. Initialized an counter to 0 and all elements of array to 0. For each new position of k*k square I increased counter++. And for each CC i checked if array[curr_cc]==counter
if(array[curr_cc]==counter that means this cc has been counted for curr k*k square if(array[curr_cc]!=counter) { add curr_cc elements to sum;array[curr_cc]=counter;}
code for ref: http://www.codeforces.com/contest/680/submission/18346981
I am trying to implement a solution along the lines of the first solution mentioned for Bear and Square Grid( Div1 C). I am unable to debug my solution. Can someone look into this: http://codeforces.com/contest/679/submission/18348818
There may be O(n2) connected components.
int cc_size[maxn];->int cc_size[maxn*maxn];int cnt[maxn];->int cnt[maxn*maxn];Thanks a lot :)
In 679A, maybe it should be
printf("%d\n", a);in the solution code. ;-)For some reason I can't use a character
\in codes in blog.Try double
\i.e.\\I tried it many times. It even works in preview but not after posting. Btw. cool profile pic.
LOL. Many people say it's dog. :D Thanks. :)
Beautiful problems, brilliant editorial and elegant codes. Thanks a lot Errichto
Magic in 679D - Bear and Chase is really beautiful!
I think cf should add a new tag for problems as "magic" or "order proof" :D
When I am running my code on ideone for the input: 994 output is: 12 941, but when I submit here its output is 12 940. please check this bug in your testing. This is the ideone link to my code: http://ideone.com/DEY8jw
Don't use
pow()for integers.In problem 679D editorial, you said "in vector
interestingstore all cities that are at a distance d1 from g1", maybe you actually meant "in vectorinterestingstore all cities that are adjacent to cities that are at the distance d1 from g1"?Can some one please tell in Div1 B question why small m2 is worse , if we consider m2 = 7 and m2 = 8 , here m2 = 7 will have high count.