Hi again!
If you notice typos or errors, please send a private message.
688A: Opponents
Solution
Let's find out for each row of the given matrix if it is completely consisting of ones or not. Make another array canWin, and set canWini equal to one if the i-th row consists at least one zero. Then the problem is to find the maximum subsegment of canWin array, consisting only ones. It can be solved by finding for each element of canWin, the closest zero to it from left. The complexity of this solution is O(nd), but the limits allow you to solve the problem in O(nd2) by iterating over all possible subsegments and check if each one of them is full of ones or not.
688B: Lovely Palindromes
Hint
Try to characterize even-length palindrome numbers.
Solution
For simplifications, in the following solution we define lovely integer as an even-length positive palindrome number.
An even-length positive integer is lovely if and only if the first half of its digits is equal to the reverse of the second half.
So if a and b are two different 2k-digit lovely numbers, then the first k digits of a and b differ in at least one position.
So a is smaller than b if and only if the first half of a is smaller than the the first half of b.
Another useful fact: The first half of a a lovely number can be any arbitrary positive integer.
Using the above facts, it's easy to find the first half of the n-th lovely number — it exactly equals to integer n. When we know the first half of a lovely number, we can concatenate it with its reverse to restore the lovely integer. To sum up, the answer can be made by concatenating n and it's reverse together.
The complexity of this solution is  .
.
Challenge
What if you were asked to find n-th positive palindrome number? (1 ≤ n ≤ 1018)
687A: NP-Hard Problem
Hint
Try to use all of the vertices. Then look at the two vertex covers together in the graph and see how it looks like.
Solution
Looking at the two vertex covers in the graph, you see there must be no edge uv that u and v are in the same vertex cover. So the two vertex covers form a bipartition of the graph, so the graph have to be bipartite. And being bipartite is also sufficient, you can use each part as a vertex cover. Bipartition can be found using your favorite graph traversing algorithm(BFS or DFS). Here is a tutorial for bipartition of undirected graphs.
The complexity is O(n + m).
Challenge
In the same constraints, what if you were asked to give two disjoint edge covers from the given graph? (The edge covers must be edges-disjoint but they can have common vertex.)
687B: Remainders Game
Hint
Assume the answer of a test is No. There must exist a pair of integers x1 and x2 such that both of them have the same remainders after dividing by any ci, but they differ in remainders after dividing by k. Find more facts about x1 and x2!
Solution
Consider the x1 and x2 from the hint part. We have x1 - x2 ≡ 0 (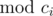 ) for each 1 ≤ i ≤ n.
) for each 1 ≤ i ≤ n.
So:
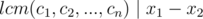
We also have 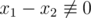 (
(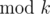 ). As a result:
). As a result:
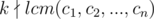
We've found a necessary condition. And I have to tell you it's also sufficient!
Assume 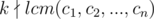 , we are going to prove there exists x1, x2 such that x1 - x2 ≡ 0 (
, we are going to prove there exists x1, x2 such that x1 - x2 ≡ 0 (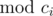 ) (for each 1 ≤ i ≤ n), and
) (for each 1 ≤ i ≤ n), and 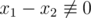 (
(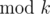 ).
).
A possible solution is x1 = lcm(c1, c2, ..., cn) and x2 = 2 × lcm(c1, c2, ..., cn), so the sufficiency is also proved.
So you have to check if lcm(c1, c2, ..., cn) is divisible by k, which could be done using prime factorization of k and ci values.
For each integer x smaller than MAXC, find it's greatest prime divisor gpdx using sieve of Eratosthenes in 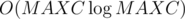 .
.
Then using gpd array, you can write the value of each coin as p1q1p2q2...pmqm where pi is a prime integer and 1 ≤ qi holds. This could be done in 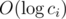 by moving from ci to
by moving from ci to 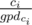 and adding gpdci to the answer. And you can factorize k by the same way. Now for every prime p that
and adding gpdci to the answer. And you can factorize k by the same way. Now for every prime p that 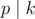 , see if there exists any coin i that the power of p in the factorization of ci is not smaller than the power of p in the factorization of k.
, see if there exists any coin i that the power of p in the factorization of ci is not smaller than the power of p in the factorization of k.
Complexity is 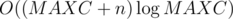 .
.
And a nice implementation by Reyna: 18789803
687C: The values you can make
Hint
Use dynamic programming.
Solution
Let dpi, j, k be true if and only if there exists a subset of the first i coins with sum j, that has a subset with sum k. There are 3 cases to handle:
- The i-th coin is not used in the subsets.
- The i-th coin is used in the subset to make j, but it's not used in the subset of this subset.
- The i-th coin is used in both subsets.
So dpi, j, k is equal to dpi - 1, j, k OR dpi - 1, j - ci, k OR dpi - 1, j - ci, k - ci.
The complexity is O(nk2).
Challenge
In the same constraints, output the numbers you can never not make! Formally, the values x such that for every subset of coins with the sum k, there exists a subset of this subset with the sum x.
687D: Dividing Kingdom II
Unfortunately, our mistake in setting the constrains for this problem made it possible to get Ac with O(qm) solution. We hope you accept our apology.
Hint
Consider the following algorithm to answer a single query: Sort the edges and add them one by one to the graph in decreasing order of their weights. The answer is weight of the first edge, which makes an odd cycle in the graph. Now show that there are only O(n) effective edges, which removing them may change the answer of the query. Use this idea to optimize your solution.
Solution
First, let’s solve a single query separately. Sort edges from interval [l, r] in decreasing order of weights. Using dsu, we can find longest prefix of these edges, which doesn’t contains odd cycle. (Graph will be bipartite after adding these edges.) The answer will be weight of the next edge. (We call this edge “bottleneck”).
Why it's correct? Because if the answer is w, then the we can divide the graph in a way that none of the edges in the same part have value greater than w. So the graph induced by the edges with value greater than w must be bipartite. And if this graph is bipartite, then we can divide the graph into two parts as the bipartition, so no edge with value greater than w will be in the same part, and the answer is at most w.
Let's have a look at this algorithm in more details. For each vertex, we keep two values in dsu: Its parent and if its part differs from its parent or not. We keep the second value equal to "parity of length of the path in original graph, between this node and its parent". We can divide the graph anytime into two parts, walking from one vertex to its parent and after reaching the root, see if the starting vertex must be in the same part as the root or not.
In every connected component, there must not exist any edge with endpoints in the same part.
After sorting the edges, there are 3 possible situations for an edge when we are adding it to the graph:
The endpoints of this edge are between two different components of the current graph. Now we must merge these two components, and update the part of the root of one of the components.
The endpoints of this edge are in the same component of the current graph, and they are in different parts of this component. There is nothing to do.
The endpoints of this edge are in the same component of the current graph, and they are also in the same part of this component. This edge is the "bottleneck" and we can't keep our graph bipartite after adding it, so we terminate the algorithm.
We call the edges of the first and the third type "valuable edges".
The key observation is: If we run above algorithm on the valuable edges, the answer remains the same.
Proof idea: The edges of the first type are spanning trees of connected components of the graph, and with a spanning tree of a bipartite graph, we can uniquely determine if two vertices are in the same part or not.
So if we can ignore all other edges and run our algorithm on these valuable edges, we have O(n) edges instead of original O(n2) and the answer is the same.
We answer the queries using a segment tree on the edges. In each node of this tree, we run the above algorithm and memorize the valuable edges. By implementing carefully (described here), making the segment tree could be done in 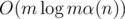 .
.
Now for each query [l, r], you can decompose [l, r] into  segments in segment tree and each one has O(n) valuable edges. Running the naive algorithm on these edges lead to an
segments in segment tree and each one has O(n) valuable edges. Running the naive algorithm on these edges lead to an  solution for each query, which fits in time limit.
solution for each query, which fits in time limit.
687E: TOF
Hint: What the actual problem is
Looking at the code in the statement, you can see only the first edge in neighbors of each node is important. So for each vertex with at least one outgoing edge, you have to choose one edge and ignore the others. After this the graph becomes in the shape of some cycles with possible branches, and some paths. The number of dfs calls equals to 998 × ( sum of sizes of cycles ) + n + number of cycles.
Solution
The goal is to minimize the sum of cycle sizes. Or, to maximize the number of vertices which are not in any cycle. Name them good vertices.
If there exists a vertex v without any outgoing edge, we can make all of the vertices that v is reachable from them good. Consider the dfs-tree from v in the reverse graph. You can choose the edge
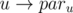 from this tree as the first edge in
from this tree as the first edge in neighbors[u], in order to make all of these vertices good.Vertices which are not in the sink strongly connected components could become good too, by choosing the edges from a path starting from them and ending in a sink strongly connected component.
In a sink strongly connected component, there exists a path from every vertex to others. So we can make every vertex good except a single cycle, by choosing the edges in the paths from other nodes to this cycle and the cycle edges.
So, every vertices could become good except a single cycle in every sink strongly connected component. And the length of those cycles must be minimized, so we can choose the smallest cycle in every sink strongly connected component and make every other vertices good. Finding the smallest cycle in a graph with n-vertex and m edges could be done in O(n(n + m)) with running a BFS from every vertex, so finding the smallest cycle in every sink strongly connected component is O(n(n + m)) overall.
Challenge
What if the target function is reversed? It means you have to choose a single outgoing edge from every node with at least one outgoing edge, and maximize the sum of cycle sizes in the chosen graph.
I thought about this one a lot but can't find any solution. Do you have any idea?











Its round 360 not 300
Fixed. Thanks!
can u explain me 687B: Remainders Game with more breifly....................
From chinese theorem (https://en.wikipedia.org/wiki/Chinese_remainder_theorem), we know that if we know the values of x%a and x%b, then we know for sure x%lcm(a, b). So in our problem if we take x%c1, x%c2 ... x%cn, if we know these values as problems says, then we know x%lcm(all ci), so if we know that value we know also x%lcm(ci)%K, so we need to check if K / lcm(all ci) is regular division with no remainder. Because of overflow we can't calculate lcm(), so we need prime factorization(I am not going to explain it now, but if you have any problem comment below)
Wikipedia said that the numbers ci should be coprime, but in the problem there is not that restriction. Does it matters?
Wikipedia also says that if numbers ci are not pairwise coprime then all solutions to the congruence system are congruent modulo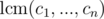 . Check again.
. Check again.
Sorry but I cannot find that sentence, can you help me please :'(
I tried to calculate LCM (c1, c2,... cn) but unfortunately the number overflowed and I got WA. In other words, I wanted to check if the LCM is a multiple of k or: GCD (LCM(c1, c2, ... cn), K) = K ?
Some accepted solutions calculate it as LCM (GCD(c1, k), GCD(c2, k), ... GCD(cn, k)) = K ?
I don't understand how both equations are equivalent?
Even i leart this after the contest:http://www.cut-the-knot.org/arithmetic/GcdLcmProperties.shtml
Here's another way of thinking:
We need to test if
so this is equivalent to the LCM containing all prime factors of k:
but we don't have to take union before intersection — we can first use intersection to kill off ones that are not prime factors of k, and then taking the union.
I got till the part where you have written that if we know x%lcm(all ci), then we know also x%lcm(ci)%K . But I couldn't understand the logic of next statement. Why should we check k/lcm(all ci). Can you please explain.
Further descriptions added to the tutorial.
thanx sir...
687B - Remainders Game can be solved using only
ints. See 18807557 (solve()at the bottom).why the time complexity of problem 688B is O(logn)?
I think that's just a typo, it should be O(n)
You are iterating over the digits of the number..not the number itself. That is why, its O(logn).
yeah, you are right.
Because it's O(length).
I think n is the number itself, not the number of digits of the number. The solution takes time proportional to the number of digits, and the number of digits is proportional to logn.
omg, what a silly question. :(
No not really, actually that same question came up for me too!
This is how one should write editorials. Thanks :)
Could you please explain div1 D? I totally don't understand why the answer to a single query is the first edge in sorted order which turns graph into not bipartite? How do we actually divide the graph?
Further descriptions added to the tutorial. I hope it's clear now.
Thanks, I somehow thought that we need to sort in ascending order and I couldn't understand how it could be true. Now it's totally clear.
Div2A can be done in O(n) using idea of kadane's algorithom .... Edit: i think i forgot to calculate complexity of strst() then it will be O(n^2) right?
Time Limit for 1B
Even the author's solution TLEs with just cin and takes 900 ms with optimized cin.
In problems which such large input (106 integers), doesn't it make sense to keep the TL greater than 1 second?
I'm sure inefficient solutions would not pass even if TL was kept at 1.5 - 2 seconds instead of 1 second.
Also, if the official solution takes 900 ms with
cinandios :: sync_with_stdio(false), shouldn't TL be at-least twice that time? Further, there wasn't a maxtest in the pretest or a warning in the question to necessarily use scanf.You might argue that there is a "lesson" to learn from all this : But the fact remains that, every once in a while when we encounter such problems, there will always be a bunch of users who will have to suffer due to this.
Many people find it convenient to use optimized
cininstead ofscanfas it works fine for almost all problems.You are right. We're sorry about this.
This happened because our C++ and java implementations work under the half of the time limit, so we didn't noticed this during the preparation. It's definitely an issue, I will pay attention to this from now on whenever I prepare a problem.
There shouldn't be a problem where scanf passes and cin doesn't, I agree.
But I can't say I understand the other side either: if you know this problem exists, why risk a whole problem because you think
cin >> ais prettier thanscanf ("%d", &a)?No one really decides to "risk the problem because cin is prettier" you now — many people who prefer cin/cout know about the issue, but it's easy to forget that in every problem with a O(n) solution you have to check if the constaints were made 106 instead of 2·105 and input/output becomes a bottleneck,
That's my point — if you always use scanf, then you don't need to check anything. If you prefer cin anyway, then you are taking risks just because it's prettier.
Starting to use scanf and printf also has its own side-effects. In Yandex Elimination Round I wrote a code for a problem and just right before submitting it (blind, without verdict), I changed cin cout to scanf printf and WRONG.... Cause output was long long and I used %d as output specifier.
Also in Round 348, I used cin/cout with
ios:sync_with_stdio(false)and got TLE. The fact was that I even didn't imagine that solution with these optimizations get TLE and I think it is definitely problem setters fault. (And the same goes for this contest too that my B failed because of this)Yesterday I didn't even think about using
scanf. I just wanted to solve the problem fast, and I always use optimizedcin, so I just did that and submitted. A few minutes before the contest ended, I realized that N = 106 and TL = 1s might be a problem. My code had passed the pretests comfortably, so I did not bother resubmitting...Problem in lovely Pallindrome
I submitted this code in java , but it shows run time error on testcase 8 , but i submitted the same code in C++ , it passes all testcases . I have just started competitive programming please help , i am not able to find what going wrong ?
First of all, please don't paste code here, you can paste your code on pastebin and post a link here or add a link to your submission.
And in your reverse function, you are adding a new character to the beginning of the string for the whole length of the original string. So, every time before adding a character all the characters are first shifted to the right by 1 place and then the new character is added in the first place. So, this has a running time of O(n^2) where n is the length of the string.
You should instead traverse the string while swapping the i'th characters from the beginning and the ending, where 0 <= i <= n / 2.
And you don't even need to write the code for this as you can use Java's StringBuilder class to do this.
I hope this helps :)
Edit : You can see how easy the code becomes using StringBuilder —
String s = in.next(); out.println(s + new StringBuilder(s).reverse().toString());This is the main code I wrote for the question :)
Thanks a lot for your reply . Okay from now on , i will use pastebin .
Thanks a lot brother . In C++, i coded it the same way & it was accepted . Can you please enlighten ?
And is it the right to take input ? (the way i have done ) .
In C++ the code got accepted as C++ is faster than Java, about 2 times as fast usually.
As you can see, even your C++ code took almost 500ms to execute so most probably your java solution also would've passed had the time limit been a little more than 1 sec.
And yes you can take input either the way you have done or by taking input character by character and then forming the variable of required data type with them, which is a little faster than your method. But even your method is very fast and you mostly should never have any time limit problem because of it.
Your Delay of publishing editorial prove you work at ysc and the delay of the second phase result of INOI is your fault.
P.S: INOI is iran national olympiad that M.Mahdi delay the publishing result about 2 months... still waiting!
P.S2: I'm using fake account, If I sent this with my own account he kills me.
Why using fake account???
Be a man, and die standing :D
Thank you!
Edit : Figured it out. Can someone clarify the meaning of valuable edges in the editorial for Div1 D: "
The edges which adding them makes change in our dsu and the bottleneck edge"Hi, I am also confused about this. What does it mean by valuable edges in div1 D, and how do you find them efficiently?
Updated. It's in more details now.
M.Mahdi can you please look at the line "So you have to check if K is divisible by lcm(c1, c2, ..., cn), which could be done using prime factorization of k and ci values." in the solution of 687B: Remainders Game as I think it is slightly confusing because we need to check whether "lcm(c1, c2, ..., cn) is divisible by K" instead of K is divisible by lcm(c1, c2, ..., cn).
It's fixed now. Thanks!
You should fix the formula standing after phrase "As a result: ..." too.
No, its Correct!
notice that when the answer in "NO" then k shouldn't be divisor of lcm(c1, c2, ..., ck)
Is complexity of Div2B log(n) with root 2 or 10?
Is log10(n). You have to make linear operations in the lenght of the string, and the string given can have up to 100000 digits, so it shoud be more or less 100000 operations.
this is maybe a very dumb question, but please answer. why up to 100000 digits? if my eyes don't deceive me, the range of input is 1<=n<=10^100000 not 1<=n<=10^5 thank you
The number of digits in 10^x is (x+1)
Why x1 - x2|lcm(c1, c2, ...) ? Wouldn't it be the oposite?
I have the exact same doubt dude!! because x1-x2 can take values of [0->Inf]*lcm(c1,c2,....);
Yes, it's fixed now. Thanks!
Thanks for fixing it dude, It really bugged me for a while now :P
Can anyone explain the idea of div1 C?
pls HELP. In problem DIV2E The values you can make,I am using the same approach as in the editorial but getting memory limit exceeded since i am using array dp[501][501][501] .How can i make changes to my code such that it passes the memory limit. My submission: http://codeforces.com/contest/687/submission/18829433 M.Mahdi EDIT 1:Got AC after using short int. EDIT 2:This can also be solved using in O(k^k) since we need only the last layer.
You can use vectors instead of arrays; or use maps or sets. The idea is to use dynamic memory instead of static memory. Anyways you can check the solution of the problem setter and see how to use less memory. (O(k*k) instead of O(n*k*k))
Just use short or char instead of int. You don't need values up to 2^31.
Got AC after using short int .Thnks. http://codeforces.com/contest/688/submission/18836648
You need only last layer of dp.
Yes we need only the last layer .BTW got AC after using short int
"In a sink strongly connected component" — do you mean "in a single strongly connected component"? That part was a bit confusing to me.
But otherwise, thanks for the editorial!
A "sink SCC" is a SCC with no edges directed towards other SCCs.
Oh I get it! Thank you for the clarification, now it is clearer to me.
I think it is wrongly written that we have to check if k is divisible by lcm(c1,c2,..cn) , it should have been the other way around , although the notation is correct.
Can you please explain how this can be implemented with this complexity?
We don't need to sort the edges in nodes of our segment tree. We can use the idea of merge sort to keep the edges sorted after merging the children of a node.
When the edges are sorted, complexity of our solution for a single query is O(nα (n) + m). We can make it in O(mα (n)) by only considering the vertices with positive degree. And each one of the edges come in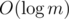 nodes of the segment tree, so this implementation is
nodes of the segment tree, so this implementation is 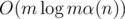 overall.
overall.
Expected solution, if I just use dsu with logN complexity gives TLE while it passes only with alpha(n). The brute solution works faster with the given constraints than the expected solution. Time limits and constraints are really bad.
Expected solution with O(logN) for dsu. TLE :
http://codeforces.com/contest/687/submission/18838352
Expected solution with O(alpha(n)) for dsu. Passes in 3.5ms. Note that segment tree is usual recursive implementation not iterative like yours.
http://codeforces.com/contest/687/submission/18838612
M*Q brute solution. Passes in 1.7ms.
http://codeforces.com/contest/687/submission/18806679
can someone help me out with recursion with memoisation solution for 687 c i used set for each node in recursion tree but it gives memory limit exceeded http://codeforces.com/contest/687/submission/18829914
I could have bet that the O(m * q) solution wasn't intended :). Nonetheless, how could you possibly differentiate an O(m) (which is, in fact, bounded by n2 / 4) solution per query, with an O(n * log(n)) solution which is itself dominated by a big constant (not to mention the fact that you have to allow more time for worse constants). It is, indeed, tricky to find constraints for such a problem.
problem 1D Don't you have to sort those n log n egdes you find in segment tree each query?
maybe a method similiar to merge sort could help
Can anyone tell me why I am getting wrong answer on test case 15. Problem 687A
http://codeforces.com/contest/688/submission/18833781
The Graph can have more than one connected component (Not all the vertices might be reachable from vertex 0)
Can anyone help me on the problem Div.2(D) Remainders Game? I'm a bit lost with the editorial since I haven't been familiar with math terminologies yet. But I understand the general idea and my implementation is kind of the same.
My idea is that, we first find X = lcm(c_1, c_2, ... c_m). Then, my thought is that, for a number from 0 to X-1, all these numbers will have different representation consists of the remainders w.r.t c_i. For example, for c_1 = 2, c_2 = 3. For 0 — 5, the representation will be (0, 0), (1, 1), (0, 2), (1, 0), (0, 1), (1, 2) respectively. From number 6, this representation repeats. So, we can think of this as a special representation of numbers, as binary, decimal, etc... but with special rules.
Then, if X is greater or equal than k(the given k), and it's a multiple of k, it should be ok to distinguish the remainders w.r.t k. But I'm getting wrong answer on test 10. Can anyone tell me where the problem is?
Here is my implementation: code
PS: by the way, how to write math formula with proper subscripts in the comment?
integer overflow is occuring while taking lcm you can add nEle=gcd(nEle,k) just after taking lcm then the code should work fine
In Div2D (or DIV1 B) Editorial,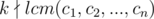
I think it should be exact opposite.
Plz correct me if I am wrong..
No, its correct.
first notice that we want to find necessary and sufficient condition for the answer "NO".
when k is not a divisor of lcm(c1, c2, ..., ck) then the answer is "NO".
because each prime factor of lcm(c1, c2, ..., ck) should have greater power than that prime factor in k.
Can you explain me anta code for 687A
jjjjj
Why is it
x1-x2 | lcm(all(ci))but notlcm(all(ci)) | x1-x2in 687B - Remainders Game when it can be shown thatx1-x2can take all values from[0->Inf]*lcm(all(ci))? P.S: I am assuming thata|bmeansa divides bplease correct me if I am wrong.I can see some people including me have misunderstood the notation.
We use the notation of three dots vertically put in order to indicate "divisible by"
We use the symbol | in order to describe "is a divisor of"
Formally, a | b means b is divisible by a.
in Div 2 Problem E (687C: The values you can make ), i calculated n*k*k value, and it was way big, and i thought that can not be the solution. I thought this speed aproximation should be around 1 million(because in linear runtime solution, n is usually 1 000 000, but now i guess it is because of slow IO speed ). Do you have an own number or different method to judge if your code will be fast enough?
10^8 operations per second has been reasonable metric for me.
Can anyone help me
Getting WA for problem C (Div 2)
http://ideone.com/3bNfFy
Actually graph might be not connected and start bfs from vertex 1 can be not enough, I think.
We don't need more than two dimension in the dp of "The values you can make" because dp[i][j][k] = dp[i][j][k] | dp[i-1][j][k] here's my solution http://codeforces.com/contest/688/submission/19469686
Can anyone,please, help with this submission Problem B (Reminder Games) WA31 http://codeforces.com/contest/687/submission/20366779
In 688E / 687C
My Top Down Solution 26136529 Didn't pass the Time Limit.
My Bottom Up Solution 26136617 Passed the Time Limit.
I thought that Top Down is always faster because it doesn't compute the states that I don't need.
So why did that happen ? xD
Apparently, you know it by now, So please tell share why it happened?
In 687B Remainders Game, it is written that lcm | (x1-x2). So, can't (x1-x2) be written as t*(lcm). Also, it says that (x1-x2) isn't congruent to 0 mod k.
So, (x1-x2) = t*lcm (t is some constant) ...1
and (x1-x2) != 0 (mod k) ...2
From 1, 2 we have (t*lcm) != 0 (mod k). But in the editorial we only check for lcm != 0 (mod k).
Why? Thanks in advance.
687D: "Using dsu, we can find longest prefix of these edges, which doesn’t contains odd cycle"
Can someone explain how you would find this using dsu? It's not obvious to me.
For the Div1 C challenge, do we only have to change the ORs to ANDs? As in this case, all paths to a subset's sum must be true, in order for it to be true. We can reach dp[i][j][k] in three ways, dp[i-1][j][k] (not using the ith element), dp[i-1][j-arr[i][k] (using the ith element, but not putting it in the subset), and dp[i-1][j-arr[i]][k-arr[i]] (using the ith element, and putting it in the subset).
In this case, dp[i-1][j][k] would mean that we can always make a subset of size k, when considering subsets of the set making up a sum of j. We can not directly use this info, as there are other ways to make dp[i][j][k] too.
So, having a similar thought for the other two dependencies, I think ANDing the three values would give the answer.
Authors, please do tell if it is the correct method, or am I lacking somewhere.
Though I am posting a comment after one year What I think should be something like this
dp[i][j][k]=(dp[i-1][j][k]AND(dp[i-1][j-c[i]][k]ORdp[i-1][j-c[i]][k-c[i]])) It might be correct as per this point, =>obtaining a sum of j using the first I elements can be done in two ways. =>1)excluding the ith element and when we exclude the ith element then we check dp[i-1][j][k].
=>2)including the ith element and then we check (dp[i-1][j-c[i]][k]|dp[i-1][j-c[i]][k]). =>an OR operation in the second case because the subset we are considering is on the same fact including the ith element so either this subset was already having one of its subsets with sum k or one of its subsets with sum k-c[i] which would become k.
Hello can someone explain why I got a TLE on case 14 on Div1 A even though I did the same thing as the tutorial said?
Link: https://codeforces.com/contest/687/submission/89819023
(I use Java btw)
Chinese Remainder Theorem an Errichto youtube lesson lesson