Hello everyone!
My friend and I were discussing range update and range query of maximum in two dimensions and I am not sure how to implement such a data structure. It appears to be much more difficult than range query/update in one dimensions as it is hard to propagate a tree.
Can anyone provide any insight on this?
Thanks in advance











It's impossible to achieve log^2 worst case time complexity. But you can use quad tree instead, which gives O(N) per update/query.
?? But there is 2D segment tree for queries with such complexity... += and sum on range are possible with log^2 complexity.
Can you handle other types of queries apart from submatrix-sum queries (with range updates) using 2D Segment Trees in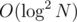 ? Something like max or min?
? Something like max or min?
Personally I can't even handle += and sums :)
I just know that it's possible
That's a much too strong statement to be left with positive number of votes and without evidence at the same time.
Comment ratings on Codeforces rarely make any sense
Sum queries can surely be handled with updates in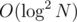 .
.
Max/Min seems hard.
I was talking about max/min, though what you are talking about is not what is usually called 2d-queries.
What you have done allows to perform rectangle queries and updates on 2d-array of size, like, 1000x1000.
But the more common problem is when you have, like, 105 points in the plane with arbitrary coordinates, each point is assigned with some weight and you are asked to perform two kinds of queries: getting sum of weights of all points belonging to a rectangular region and increasing weights of all points belonging to a rectangular region by some constant.
This also can be done in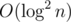 per query, but I only know an approach that requires
per query, but I only know an approach that requires 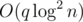 memory and that is completely inefficient. The best choice for such a problem would be using an sqrt-decomposition rather than a log2n approach.
memory and that is completely inefficient. The best choice for such a problem would be using an sqrt-decomposition rather than a log2n approach.
But what exactly is wrong with nested BSTs solution? Its space requirement would be .
.
Hi! Your link has been corrupted. Could you update it or give some information about sum queries?
Yes max and min functions are also possible.
Edit: I haven't seen that it's with updates. No 2d segment trees can't handle 2d rectangle updates. As each row update will have different cols ranges so lazy propagation can't be applied.
Add submatrix and query sum of submatrix can be supported using 2D BIT (thus possible using 2D segment tree). But I believe add submatrix and get max on submatrix cannot be done the same way as the 1D case, and quadtree is the best I know for such cases.
But Quad tree is for square grid n*n
not for n*m
Well, simply view the matrix as max(m,n) * max(m,n) if you want :)
In fact quadtree is built separately on each dimension, so you don't have to make sure the matrix is square.
http://codeforces.com/blog/entry/45157
Hi !
Problem Tetris 3D require a 2D segment tree with update and query on range (it is what you need).
It is possible !
We need 2 segment tree (one main and other for lazy propagation) that every node of this segment trees has 2 segment trees; one main and other for lazy propagation.
It has a log^2 worst case time complexity.
See my code for better understanding.
I've inspected your code:
How exactly is this specific? It seems to me that it fully solves the problem of:
If you mean that the updates have to come with increasing values of $$$v$$$, I think you're wrong (or at least, it seems to work ok to me for arbitrary $$$v$$$).
Moreover, it seems that a lot of modifications are possible, including rectangle add value + rectangle sum query, which I for once thought to be very hard, if not impossible. Also, it seems to be able to be adapted easily to $$$x, y \leq 10^9$$$, which is just WOW.
Not to mention that it seems that it can naturally be extended to an arbitrary number of dimensions (in complexity $$$O(log^D(MAX))$$$).
I think this is an awesome technique, and it fully deserves to be appreciated.
Fun fact: it uses the technique of "lazy without propagation" that I've described here some time ago, which, ironically, a handful of people (me included) thought that it wasn't that useful, along with the awesome observation that you can update a node in a segment tree without having to "combine" information from the two children (which would be impossible in 2D). These two things seem to allow 2D segment trees that can do a lot of the "lazy propagation" operations.
[UPDATE] Found a paper: https://arxiv.org/pdf/1811.01226.pdf
It's inaccurate for the paper to claim that it "is capable of performing any general aggregate function similar to the original Segment Tree" :/
Solving rectangle add value + rectangle sum query has been mentioned several times though:
The first link gives me 404.
The second link seems to describe fenwick trees with the linear function trick which is not trivial at all to implement for some people (I’ve never implemented myself the 1D version of it, as it feels too sketchy, compared to segment tree). Also, I would rather pick 2D segment trees than 2D BITs for inputs with higher coordinates (as 2D BIT with hash map would probably be very slow).
The last comment does indeed describe this technique, but IMHO it’s still not convincing enough that people actually know about this idea.
It is specific in the way you've described: it works for $$$M(x, y) \leftarrow max(M(x, y), v)$$$, but doesn't seem to work for $$$M(x, y) \leftarrow v$$$. The former updates are monotone, the latter are not.
By the way, I'm not saying that the technique is useless. It's just that we shouldn't call it "lazy propagation".
I do recall the problem and it seemed quite particular (as in I think you were using the fact that updates are monotone). Either way, the only truly nice thing about it is that the query you perform is for a non-invertible operator, and therefore you have to build the maximum constructively.
I'd be curious to see if any results are known about this sort of operators, but the paper seems to exemplify an approach for sums only, if I'm not mistaken (and well other operators alike).
Invertible, associative and commutative operators should be super easy compared to this if you consider 2^D cases (for D the dimension of the problem) on both updates and queries and some formulas here and there.
I might be missing something here, but how exactly are invertible, associative and commutative operators super easy? Do you refer to using 3 2D fenwick trees?
This approach seems to work with arbitrary non-invertible operators, as long as they are associative and commutative (on all axes). Setting a value is non-commutative, therefore it doesn’t work.
Just to be clear, the problem here is solving (online):