I never thought Kuhn-Munkres would strike me that hard...
How to solve F L? And what was intended for H?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
| Name |
|---|



How to A, C, D, J? :D
J: For each edge suppose that there are a persons on the on side and 2m-a persons on the others side. Then it will be used in min(a, 2m-a) pathes. So, iterate over edges, and over a and multiply C(2m, i)·vi·(n - v)(2m - i)·edge·min(i, 2m - i) where v is the number of vertices on one side of the edge
C: Let x_0 = 0, and x_i is how much down will i-th component drop. Then for each two consecutive # is one column we get equation of form xj < = xi + C (and for the lowest one xi < = x0 + C. This inequalities can be solved using Dijkstra.
Could you please share your implementation with Dijkstra? Mine got TL, so I had to remove log n factor by using n vectors instead of set (since the distances are at most n).
We also had no log n factor via n doubly linked lists.
code: https://ideone.com/4URZio
author: zemen
Works in 1.279s on 5th test, all other testcases < 0.6s
Seems to be usual dijkstra on priority queue
Actually I used SPFA so I had nm (maybe n+m) factor... My modeling had edge with C<0. I couldn't figure out how to fix it but just wrote that
https://pastebin.com/qSZ9aE0J
Dijkstra with std::set, works 1.24 on 5th test.
Thanks! The reason for my TL was that I inserted all vertices into std::set at the beginning (obviously not too clever). Now that I only insert the starting vertex first, it passes in 1.2 seconds as well.
The author's solution is similar to this, but a bit more simplified. Instead of having a vertex for each component, there is one for each cell in the matrix. Now all edges in this graph have either C = 0 or C = 1 allowing for a very easy O(N * M) implementation (and creating the graph is easier to implement too).
D: somewhat straight-forward case-analysis (the problem is to write this cough code).
Can you explain how to solve D in more details?
A: That was solved without me, but solution is hungarian algo on matrix - A
I want to participate in next GPs, but I don't know how, can someone help me ?
L:
First, find the xor of all numbers. If it's 0, it's a draw. If not, find its highest 1 bit, and then we only need to look at this bit, so we reduced our problem to n zeroes and ones, with odd number of ones. The player to grab an odd number of ones wins.
Now, if n is even, the first player wins, because he can guarantee all black or all white squares in an alternating coloring, and one of those must have an odd number of ones.
When n is odd, if the first player grabs a zero, he loses by the above argument. In the following game, the first player must always grab the same number as the second player, otherwise he will again lose by the above argument. So his only chance is to always repeat the move of the second player, an only in case half of all ones after the first move is even.
Now, when can he always match the moves of the second player? I claim that when what remains after his first move looks like this: ABA', where A' is a reverse of A, an in B all numbers come in pairs (i.e. 001111001100).
The proof of this last statement is not yet very formal in my head.
After move of the first player length of sequence is even. Seems that it could be reduced to empty string by operations of removing two neighboring equal numbers.
But not every string that is reducible in this manner is winning for the first player. For example, consider
100100100001
Here the second player wins because he keeps taking from the left end, and obtains either 100100 or 10010000, at which point he wins by taking 1 and first player can not repeat.
You are right, my bad.
Wow, tricky...
where can i find these problems?
It seems you can find them here http://opentrains.snarknews.info/~ejudge/index.cgi
What about B, I and K?
K: Suppose we have odd number of "corners" then base figure is
otherwise base figure is
now, we can add to either top or bottom side pairs of corners:
then, rest of triminos, dominos, and cells (in that order), adding each figure to the currently shorter side. It may be proven that it'll always work.
code is ugly but actually easy to write
B (by ilyakor):
Let's do backtracking column by column. For each column, if we choose some number, then we also immediately determine the number for all rows that have some other number in this column. And that, in turn allows us to determine the values for some other columns on the right of the currently processed one. Finally, if we choose a number that is not present in this column, then we determine all rows, and can stop backtracking and take k to the power of the number of yet undetermined columns.
More precisely, we remember the following during backtracking: we have chosen the numbers for the first x columns and some subset of rows, and for some of the remaining columns the already processed rows require a specific color.
If we start off by having n rows, then we branch at the first column into several recursive calls with n1, n2, ... rows such that n1+n2+...=n. So if inner processing inside one recursive call takes O(nm) where m is the number of remaining columns, then the overall running time is given by f(n,m)=O(nm)+f(n1,m-1)+f(n2,m-1)+..., which means f(n,m)=O(nmm).
Doing the internal processing in O(nm) is not entirely straightforward as naively we would iterate over the entire matrix for every candidate color, but can be done using some standard counting tricks taking advantage of the fact that different colors have a big common part of processing.
I: Dynamic programming where states are pairs (j, k), where i is the number of strongly connected components and k is the number of "free" edges. A transition either adds a free edge, or uses the new edge along with some free edges to merge strongly connected components with a cycle.
After we reach edges, it is impossible to keep n strongly connected components, with similar conditions for smaller counts of connected components. We need to remove all states with
edges, it is impossible to keep n strongly connected components, with similar conditions for smaller counts of connected components. We need to remove all states with 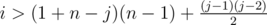 (where i is the total number of edges).
(where i is the total number of edges).
This DP has complexity O(n6), and can be optimized to O(n4).
code
D is almost the same as this (decimal instead of binary), but test data for D is stronger than this past problem. You might not get AC only by copy-pasting and changing some "10"s into "2"s.
F: consider a range [L, R] of values in the first array so that everything outside it will be removed in the final answer. Clearly, the number in the range must form an increasing subsequence.
Let x and y be the numbers immediately below and above [L, R] in the first array respectively. The play will then proceed as follows: first erase all the numbers at least y, then erase all numbers at most x (or vice versa). The optimal strategy is to insert numbers from [x, y] as long as possible, then (assuming we are currently trying to erase larger numbers) insert smaller elements, effectively increasing the number of smaller elements to be deleted later. We can predict the number of moves required for each phase in O(1) just by the number of elements inside the range and to either side of it.
Finally, only ranges that are non-extendable to either side should be considered, which makes for an , or even an O(n) solution.
, or even an O(n) solution.
How do you guys find these GPs ? I don't see them on any calendars nor any announcement blog. Or are they private contests ?
You can find the problems here http://opentrains.snarknews.info/~ejudge/index.cgi
How to solve E?