Here's a technique to do C — New Year and Curling in  time with segment tree. Brute force n2 is of course fast enough, but I think speeding it up was interesting.
time with segment tree. Brute force n2 is of course fast enough, but I think speeding it up was interesting.
Suppose we are about to place disk i at xi. The relevant x range we should look for disks is [xi - 2r, xi + 2r] because things outside of this range are too far away to intersect with this disc. Say we find j such that j < i, xj is in the needed range, and yj is maximized. We can find such j with a basic segment tree in 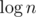 time. The intuition behind the
time. The intuition behind the  approach is that
approach is that 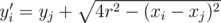 is a good lower bound for yi. Specifically, yi < yi' + 2r as shown by the diagram:
is a good lower bound for yi. Specifically, yi < yi' + 2r as shown by the diagram:
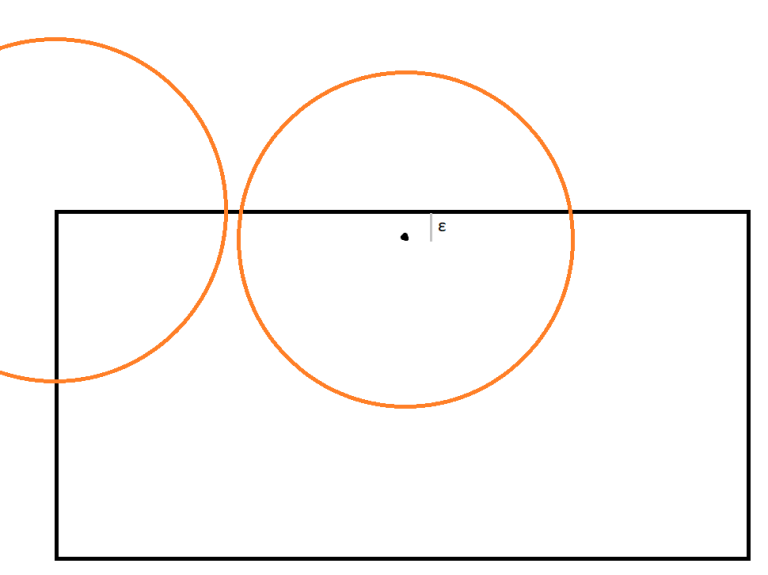
In this worst case scenario we find that disk j corresponds to the left disk. However, another disk is centered at (xi, yj - ε). So yi' in this case is yj but the true answer is yj + 2r - ε. If we could find the second-highest circle with our segment tree, we'd get the answer right in this case. We can do this by first querying [xi - 2r, xi + 2r] and getting back a result xq1. Assume xq1 < xi (the other case is symmetric); we next query (xq1, xi + 2r]. Say this second query result is xq2 with xq2 > xi (again other case is symmetric); we next query (xq, xq2) to get the third-highest circle. If we do this just a few times we're guaranteed to get the right answer.
The reasoning behind this is that a constant number of circles fit in the "relevant area," regardless of what n or r are. The relevant area is a 4r x 2r rectangle horizontally centered at xi and with the top y value yq1. It's the black box in the diagram above. If a disk's center is horizontally outside this range, the disk won't intersect the query disk. If the disk is below the relevant area, it's too low to matter (yi' is higher). And no disk can be above this area because of how yq1 is defined. The relevant box has area 8r2, and any circle centered in it must occupy at least π r2 / 4 area, so at most 10 circles inside of the box. So, if we do our procedure 10 times (so 10 segment tree queries), we're guaranteed to get the answer. 10 is a pretty loose bound and I got AC with 4.











Auto comment: topic has been updated by sammyMaX (previous revision, new revision, compare).