Is there a polynomial algorithm to find a spanning tree of an undirected grid graph which minimizes the number of turns in tree? A turn is when there are two edges connected to one vertex which have perpendicular directions.
In this problem we have arbitrary set of cells in grid which form a connected graph (not only rectangles are considered). Thus, set of cells may form concave areas and areas with holes
For example, given a 4 x 4 grid graph (see image below), we want to find a spanning tree like that on the right (which has 6 turns) rather than that on the left (which has 14):
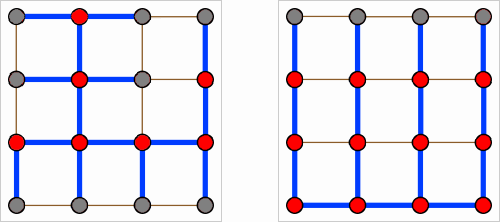
Ideas about approximate algorithms may be useful too.











I think the spanning tree like one that on the right is always optimal
But cells in the grid form not always a rectangle. For example, for Г-shaped set of cells the optimal tree is
г------------------
г------------------
гттт--------------
||||||
||||||
||||||
||||||
H-shaped grid is more difficult
But that's not a grid graph?
Subset of cells in grid?
Auto comment: topic has been updated by shaviava (previous revision, new revision, compare).
approximation algorith: first make vertical, after that horizontal edges and merge with dsu just like kruskal's.
The expanded problem of this problem has already been taken here and can be solved using the Kruskal method.There is editorial on the link.(It is considered only when it is a rectangle) Even when it is not a rectangle, I think that it can be solved by the usual Kruskal method by setting the cost of the edge between adjacent vertices to 1.
There was a simple mst, but I want to minimize numbers of turns. And I can't reformulate this problem in terms of problem from atcoder