Rating changes for last rounds are temporarily rolled back. They will be returned soon. ×

Lakh's blog

Is RMQ possible using one Binary Indexed Tree?
By Lakh, history, 6 years ago, In English

I read the approach for finding Range minimum value using 2 Binary Indexed Trees. Is it possible to do this problem using only one BIT when updates are also there?

  • Vote: I like it
  • +5
  • Vote: I do not like it

Comments Comments (7)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

No, a normal BIT is only able to answer prefix RMQs. A BIT doesn't have enough information to answer a general RMQ (as it doesn't even store the value of each element).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -19 Vote: I do not like it

    You sure?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +1 Vote: I do not like it

      I have read this paper previously .In this paper two BITs have been used . I want to know if we can achieve the same result using a single BIT.

      → Reply
»
6 years ago, # |
  Vote: I like it +12 Vote: I do not like it

Found one approach for solving RMQ using BIT(without updates). Suppose our query range is [L,R]. We know that BIT[i] stores the result from index [i-(i & (-i))+1] to index i.

So for given query we start from R. Now first we check if index [R-(R & (-R))+1]>=L or not. if yes we just update the minimum value using the value in BIT[R] and update R by subtracting (R & (-R)) from R . if not then we just take minimum of A[R] and current answer and update R to R-1.

We keep on doing this while(R>=L).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +20 Vote: I do not like it

    This algorithm will return the correct result but cost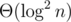 time complexity if you query the range [2, n].

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Can you provide some explanation for this complexity. Not able to get it.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Firstly R will go to the biggest 2k satisfying 2k ≤ n, then the progress will be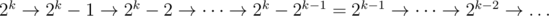 , between the progress it would take k times. So the total time complexity is Θ(k2).

        → Reply