mohamedeltair's blog

Number of permutations of length N which have at least one increasing sub-array of length M?
By mohamedeltair, history, 6 years ago, In English

The problem is simply as the title says, 1<=N<=200 and 1<=M<=N. The number of permutations is required mod 1e9+7. I thought of multiple methods but I am stuck in each one of them:

1) For each position i, calculate ans[i], where ans[i] is the number of permutations which have at leasing one increasing sub-array of length M starting at i and don't have any increasing sub-arrays of length M starting at positions earlier than i. The final answer is sum of all ans[i]. But I can't calculate ans[i] properly (stuck at the part of ensuring that ans[i] doesn't include any increasing sub-arrays of length M starting at positions earlier than i).

2) calculate ans[x] for 1<=x<=M or M<=x<=N (as ans[1] = N! and ans[N] = 1). But I can't find a way to calculate ans[x] from ans[x+1] or from ans[x-1].

3) Find the answer using dynamic programming with state dp[i][j][k][l], where i is the current position, j is last number put, k is the length of longest increasing suffix, l is boolean representing whether an increasing sub-array of length M has been constructed or not. But I can't ensure that the new number I will try to put at position is is not put before at an earlier position.

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
6 years ago, # |
← Rev. 2   Vote: I like it +22 Vote: I do not like it

I have a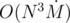 solution which might be enough; anyway, I think it can be optimized with prefix sums or something like that for better complexity.

dp[i][j][k] -  state of a permutation where the i-th first numbers are already chosen, j numbers smaller than the i-th one are free to be used and there is a increasing subarray ending at element i with length k.

If k = m, then you might just return factorial(n - i), i.e. just choose the n - i last elements in any way. Otherwise, you have two options for the (i + 1)-th element: either it is greater than the i-th element or it is smaller. Note that the quantity g of numbers greater than the i-th one which are free to be used is simply (n - i) - j. Now, you can make the transitions in O(N):

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +17 Vote: I do not like it

    By doing partial sums on diagonals (for g) and rows (for first part of the sum) you can do the transitions in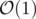 achieving .

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

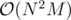    @fofao_funk Thanks a lot for your easy-to-understand answer

    @radoslav11 Thank you for the optimization

    → Reply