Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
| Name |
|---|



Auto comment: topic has been updated by kristevalex (previous revision, new revision, compare).
1068c is probably not what you wanted to post
Why not? It is not div1A, editorial for div1A is not ready yet
Ok, I missed that the number of problems is unusual
Kindly post for 1068D Thanks!
edit: never mind
I think, that in your solution there is no square that is beaten by 4 initial rooks.
Another solution of 1067D - Computer Game:
It's clear that we will play one quest (for example 1st) until win, then upgrade another (or the same) quest (for example 2nd), and play the 2nd quest all the time.
Math expectation of the score: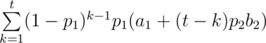
Let's simplify this formula using wolframalpha.com.
Result: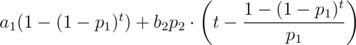 .
.
Let's denote:
So answer is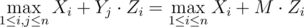 where M = max Yi.
where M = max Yi.
Complexity: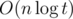 .
.
So this problem can be solved using wolframalpha.com. I am not proud of myself but I think this is a downside for this problem.
Got wa105
But why is it wrong?
That's a wrong assumption.
Suppose you have something like
If you're unlucky (got 9 fails on first quest) you'd have to switch to quest 2 for last attempt.
It's almost right though. When there is one turn left and you're still not upgraded just try the one with the best a[i]*p[i].
I got accepted after contest :(
I don't think that's correct solution. You should choose max of several linear functions each time which is basically to build convex hull. It's a shame it gets AC.
Yes, our tests are really bad. We had a test where you have to use around 20000 different quests and I was shocked to see that such stupid solution passes it. But it turned out that due to the fact that at the start you will use quests with highest probability, after some time the probability of not completing one quest is so small that it is not important what you'll do next.
Yeah, it was probably hard to fail without requiring modulo arithmetic
Cool, almost every solution for div1D got WA105
lol I've just noticed that this is last test.
Problem div2. D was easier than div2. C. Fairly straightforward DP. Problem C was harder partially due to it's language, difficult to understand.
This may simply be due to your predispositions — I found problem C relatively simple and even problem E easier than problem D, but I come from a maths background and am not as practiced in DP problems for example.
I feel the problem was more of observation that working out math in it.
Anyways, What kind of math courses have you studied, high school mathematics or anything else?
Yes, but finding examples/constructions is something often done in combinatorics which helps you out massively.
No specific courses, but I participated in IMO 2017, 2018 for Croatia. :)
The amount of people who solved C D E confirms this is common. It is the same for me aswell
For div2. C, the total number of rooks used should be n + m in the editorial. kristevalex
Unfortunately the system tests on today's Div 1 problem D were quite weak. I wrote up an explanation here: https://codeforces.com/blog/entry/62692. Make sure to take a look if you are trying to solve problem D in practice mode (or just interested in the problem).
A fast editorial.
A punctual editorial, great! Looking forward to solution for Div.1 C
After that we can find middle vertex in diameter and check if it is a center of k-multihedgehog using simple dfs.Can anyone please explain how to check?
Start the dfs from the center. For any non-leaf node check the degree to be strictly greater than 3. Check if all leaf nodes are at the same depth. One exception: center degree should be greater than equal to 3.
I mistakenly thought that the degree of non-leaf node except center can be equal to 3 as well. That was wrong.
Thank you :)
Someone can tell me what's wrong with my Div2 solution.C (1068C)? First I build a diagonal of rooks (1, 1), (2, 2), ... (n, n). Then for each connection a-b I put one rook of color min (a,b) on the cell (min(a, b), max(a, b)). My decision (https://codeforces.com/contest/1068/submission/44806161) got WA4
Got the wrong answer in 1068_A because I used
ceil()function inC++.Lessons learnt: Never ever use inbuilt
ceil()function. Instead use(a+b-1)/bThat's not the lesson you should have learned though. The proper lesson is: "Never use floating point calculations when you intend to work with integral numbers"
yep. agree with you :D
How would you solve Div2C if the limit of 1000 on total edges was removed? I actually missed this detail and made the question really hard for myself. That would mean you cannot use more than n+m rooks in the worst case.
Deleted.
You are also using n+2*m rooks...please check your solution again.
I have a different (imo simpler) way to find the expected size of the maximal matching in problem E. You don't need a DP to find the maximal matching in a tree. If we root the tree somewhere and construct the maximal matching bottom up there is no reason not to greedily match nodes that have an unmatched child.
Root the input and let f(v) be the probability that if we perform our greedy algorithm on the (random forest generated from the) subtree rooted at v, node v will be matched with one of its children. By linearity of expectation, the expected number of edges in the maximal matching is equal to the sum of f(v) over all v.
f(v) can be computed with a standard tree traversal:
You can see my implementation here.
Can someone please explain 1067A — Array Without Local Maximums , i am unable to understand it from the editorial
We want to use dynamic programming to solve the problem, because it seems as if the only relevant results are in the last 2 columns. If we know all ways to get a number from the last two columns, then we can fill in the next column. The process is like so: for each way to go through the two columns (suppose we use elements i, then j), we have 2 cases.
Case 1: i<j, then we can go to any of the elements from j to n in the next column.
Case 2: j>=i, we can go to any of the elements,
Note, we don't care about the value of i, only if the array is increasing or decreasing. So we only need to know information about the last row and if it is increasing or not. We can store it in a dp, but we now need to store if it is increasing or decreasing in this dp. To record this, we will add to what we do for each case.
Case 1: We will still add all elements from j to 200. It will be increasing for all elements besides when we go from j to j.
Case 2: We will still add all elements. It will be decreasing if we are going to elements from 1 to j.
To increase speed: Rather than count all ways each time, store values from prior calculations. For example, the # of ways to go to element 4 from the last array while increasing = (ways to get 3 in last array) + (ways 2 in last array) + (ways 1 in last array). If we iterate from 1 to 200, we can store these last 3 parts in a sum so we don't have to recalculate them each time. This might mean that your code won't look exactly like the two cases above.
Anyways, now you're done. The boundary conditions can be dealt with by putting the start of the dp as case 1 and only looking at case 2 in the end.
Commented Code: http://codeforces.com/contest/1067/submission/45311578
Editorial for Div2 D is so poorly written... Can anybody help?
Is there any way to reduce complexity of my recursive dp solution from O(n*a^2) to O(n*a). Here is my solution for question 1068D or 1067A
For problems like Div1.C, I am curious if there are some efficient ways to make sure our construction works for small n.
Did anyone write the solution 1 for Div1B / Div2E ?
I tried implementing it but got WA 89. Can somebody find out what's missing? Submission
In question 1068B I submitted two solutions https://codeforces.com/contest/1068/submission/220826372 and https://codeforces.com/contest/1068/submission/220826179 both are quite similar only for the difference of a bracket but the first submission gave me AC while the second one TLE. can anyone help me find the reason for this?