Hi there!
I recently thought up a very interesting problem, so I will introduce it to you guys.
One day, when I (Dreamr) was in the pool teaching a swimming lesson held in the neighborhood pool center, I was thinking about the inefficiency of the process for the upcoming exam. There are n (1 <= n <= 100,000) pools in the swimming center and m(1 <= m <= 100,000) students who would participate in the exam.
Dreamr, the owner of the center, already knew about the duration (every di <= 10^9) of each student that will take the exam. Only one student at a time can be in one pool and the test can be run simultaneously in multiple pools. Dreamr is a really lazy person, so he hopes to make the minimum of the maximum time of each pool's total used time. However, Dreamr is not a super bright person. Thus, Dreamr only wants to know a solution that is close to the actual answer: Your output can be smaller than or equal to 2 times the correct optimal solution. (Extra challenge: In the comments try to prove why the problem would be impossible to solve if you have to get the actual optimal solution/answer.)
Please help Dreamr solve this challenging problem.
Input
2 5
3 3 5 7 8
Output
13
3 3 7
5 8
Note
In the first test case, there are 2 pools and 5 people. If Dreamr assigns 3, 3, 5 to the first pool and 7, 8 to the second pool, then it takes 11 and 15 minutes, respectively, so the maximum time is 15. If Dreamr assigns 3, 3, 7 to the first pool and 5, 8 to the second pool, then it takes both 13 minutes, so the maximum time is 13.
13 < 15 so the optimal solution would be 13.
Thus, your output can be smaller than or equal to 26 in this case.
Sorry for my bad English <3
Thanks for reading and happy problem-solving!











how do u solve this? this is such a good problem! LOVE IT!!!!
Nice job!
Auto comment: topic has been updated by DreamR (previous revision, new revision, compare).
This problem is called multiprocessor scheduling and is NP-hard. The greedy approach where you assign each student to the pool with the lowest current total time always produces a solution that is at most 2 times as long as the optimal solution. A proof of this can be found here. The greedy can be implemented in time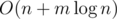 using a priority queue.
using a priority queue.