Idea: MikeMirzayanov
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int q;
cin >> q;
for (int i = 0; i < q; ++i) {
long long n;
int a, b;
cin >> n >> a >> b;
cout << (n / 2) * min(2 * a, b) + (n % 2) * a << endl;
}
return 0;
}
Idea: MikeMirzayanov
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n;
cin >> n;
vector<int> a(n);
int ePref = 0, oPref = 0, eSuf = 0, oSuf = 0;
for (int i = 0; i < n; ++i) {
cin >> a[i];
if (i & 1) eSuf += a[i];
else oSuf += a[i];
}
int ans = 0;
for (int i = 0; i < n; ++i) {
if (i & 1) eSuf -= a[i];
else oSuf -= a[i];
if (ePref + oSuf == oPref + eSuf) {
++ans;
}
if (i & 1) ePref += a[i];
else oPref += a[i];
}
cout << ans << endl;
return 0;
}
Idea: MikeMirzayanov
I should mention this blog because it is amazing! This is a tutorial of this problem from MikeMirzayanov.
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
typedef pair<int, int> pt;
const int N = 1000 + 7;
int cnt[N];
int a[20][20];
int main() {
int n;
scanf("%d", &n);
forn(i, n * n){
int x;
scanf("%d", &x);
++cnt[x];
}
vector<pair<int, pt>> cells;
forn(i, (n + 1) / 2) forn(j, (n + 1) / 2){
if (i != n - i - 1 && j != n - j - 1)
cells.push_back({4, {i, j}});
else if ((i != n - i - 1) ^ (j != n - j - 1))
cells.push_back({2, {i, j}});
else
cells.push_back({1, {i, j}});
}
for (auto cur : {4, 2, 1}){
int lst = 1;
for (auto it : cells){
if (it.first != cur) continue;
int i = it.second.first;
int j = it.second.second;
while (lst < N && cnt[lst] < cur)
++lst;
if (lst == N){
puts("NO");
return 0;
}
a[i][j] = a[n - i - 1][j] = a[i][n - j - 1] = a[n - i - 1][n - j - 1] = lst;
cnt[lst] -= cur;
}
}
puts("YES");
forn(i, n){
forn(j, n)
printf("%d ", a[i][j]);
puts("");
}
return 0;
}
1118D1 - Coffee and Coursework (Easy version)
Idea: MikeMirzayanov
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, m;
cin >> n >> m;
vector<int> a(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
sort(a.rbegin(), a.rend());
for (int i = 1; i <= n; ++i) {
int sum = 0;
for (int j = 0; j < n; ++j) {
sum += max(a[j] - j / i, 0);
}
if (sum >= m) {
cout << i << endl;
return 0;
}
}
cout << -1 << endl;
return 0;
}
1118D2 - Coffee and Coursework (Hard Version)
Idea: MikeMirzayanov
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int n, m;
vector<int> a;
bool can(int i) {
long long sum = 0; // there can be a bug
for (int j = 0; j < n; ++j) {
sum += max(a[j] - j / i, 0);
}
return sum >= m;
}
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
cin >> n >> m;
a = vector<int>(n);
for (int i = 0; i < n; ++i) {
cin >> a[i];
}
sort(a.rbegin(), a.rend());
int l = 1, r = n;
while (r - l > 1) {
int mid = (l + r) >> 1;
if (can(mid)) r = mid;
else l = mid;
}
if (can(l)) cout << l << endl;
else if (can(r)) cout << r << endl;
else cout << -1 << endl;
return 0;
}
1118E - Yet Another Ball Problem
Idea: MikeMirzayanov
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
#ifdef _DEBUG
freopen("input.txt", "r", stdin);
// freopen("output.txt", "w", stdout);
#endif
int n, k;
cin >> n >> k;
if (n > k * 1ll * (k - 1)) {
cout << "NO" << endl;
} else {
cout << "YES" << endl;
int cur = 0;
for (int i = 0; i < n; ++i) {
cur += (i % k == 0);
cout << i % k + 1 << " " << (cur + i % k) % k + 1 << endl;
}
}
return 0;
}
1118F1 - Tree Cutting (Easy Version)
Idea: MikeMirzayanov
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 300 * 1000 + 13;
int n;
int a[N];
vector<int> g[N];
int red, blue;
int ans;
pair<int, int> dfs(int v, int p = -1){
int r = (a[v] == 1), b = (a[v] == 2);
for (auto u : g[v]) if (u != p){
auto tmp = dfs(u, v);
ans += (tmp.first == red && tmp.second == 0);
ans += (tmp.first == 0 && tmp.second == blue);
r += tmp.first;
b += tmp.second;
}
return make_pair(r, b);
}
int main() {
int n;
scanf("%d", &n);
forn(i, n){
scanf("%d", &a[i]);
red += (a[i] == 1);
blue += (a[i] == 2);
}
forn(i, n - 1){
int v, u;
scanf("%d%d", &v, &u);
--v, --u;
g[v].push_back(u);
g[u].push_back(v);
}
ans = 0;
dfs(0);
printf("%d\n", ans);
return 0;
}
1118F2 - Tree Cutting (Hard Version)
Idea: MikeMirzayanov
Tutorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
#define forn(i, n) for (int i = 0; i < int(n); i++)
using namespace std;
const int N = 300 * 1000 + 13;
const int LOGN = 19;
const int MOD = 998244353;
int add(int a, int b){
a += b;
if (a >= MOD)
a -= MOD;
if (a < 0)
a += MOD;
return a;
}
int mul(int a, int b){
return a * 1ll * b % MOD;
}
int a[N];
vector<int> g[N];
int up[N][LOGN];
int d[N];
void init(int v, int p = -1){
for (auto u : g[v]) if (u != p){
up[u][0] = v;
for (int i = 1; i < LOGN; ++i)
up[u][i] = up[up[u][i - 1]][i - 1];
d[u] = d[v] + 1;
init(u, v);
}
}
int lca(int v, int u){
if (d[v] < d[u]) swap(v, u);
for (int i = LOGN - 1; i >= 0; --i)
if (d[up[v][i]] >= d[u])
v = up[v][i];
if (v == u) return v;
for (int i = LOGN - 1; i >= 0; --i)
if (up[v][i] != up[u][i]){
v = up[v][i];
u = up[u][i];
}
return up[v][0];
}
int l[N];
int dp[N][2];
int dfs(int v, int p = -1){
vector<pair<int, int>> cur;
for (auto u : g[v]) if (u != p){
int c = dfs(u, v);
if (c != 0)
cur.push_back(make_pair(c, u));
}
vector<int> vals;
forn(i, cur.size()) if (cur[i].first > 0)
vals.push_back(cur[i].first);
sort(vals.begin(), vals.end());
vals.resize(unique(vals.begin(), vals.end()) - vals.begin());
if (int(vals.size()) > 1){
puts("0");
exit(0);
}
if (a[v] != 0 && !vals.empty() && vals[0] != a[v]){
puts("0");
exit(0);
}
if (a[v] == 0 && cur.empty())
return 0;
if (a[v] == 0 && vals.empty()){
vector<int> pr(1, 1), su(1, 1);
forn(i, cur.size())
pr.push_back(mul(pr.back(), add(dp[cur[i].second][0], dp[cur[i].second][1])));
for (int i = int(cur.size()) - 1; i >= 0; --i)
su.push_back(mul(su.back(), add(dp[cur[i].second][0], dp[cur[i].second][1])));
reverse(su.begin(), su.end());
dp[v][1] = 0;
forn(i, cur.size())
dp[v][1] = add(dp[v][1], mul(mul(pr[i], su[i + 1]), dp[cur[i].second][1]));
dp[v][0] = add(dp[v][0], pr[cur.size()]);
return -1;
}
dp[v][1] = 1;
for (auto it : cur){
if (it.first == -1)
dp[v][1] = mul(dp[v][1], add(dp[it.second][0], dp[it.second][1]));
else
dp[v][1] = mul(dp[v][1], dp[it.second][1]);
}
if (a[v] == 0)
return vals[0];
return (l[a[v]] == v ? -1 : a[v]);
}
int main() {
int n, k;
scanf("%d%d", &n, &k);
forn(i, n)
scanf("%d", &a[i]);
forn(i, n - 1){
int v, u;
scanf("%d%d", &v, &u);
--v, --u;
g[v].push_back(u);
g[u].push_back(v);
}
init(0);
memset(l, -1, sizeof(l));
forn(i, n) if (a[i] != 0)
l[a[i]] = (l[a[i]] == -1 ? i : lca(l[a[i]], i));
for (int i = 1; i <= k; ++i){
if (a[l[i]] != 0 && a[l[i]] != i){
puts("0");
exit(0);
}
a[l[i]] = i;
}
dfs(0);
printf("%d\n", dp[0][1]);
return 0;
}











good contest!
nice!f2 is a interesting problem,and i learned a lot from it.
What's the proof of optimality for D for given coffee distribution-strategy ? Is it just intuitive or we can prove it ?
Yes we can prove it.The approach is greedy. Consider the caffeine values 6 5 5 3 1 1 in order and consider the distribution for 2 days and in each day you are taking 3 cups.
6 + 5 + (5 — 1) + (3 — 1) + max(0, 1 — 2) + max(0, 1 — 2) = 17
If you consider this case 6 5 1 1 3 5 in order
6 + 5 + (1 — 1) + (1 — 1) + (3 — 2) + (5 — 2) = 15
This is because in the first case max(0, -1) + max(0, -1) hides subtracting 2 from the final output.
Sorry for my bad example.
If you can bear some algebra then you can better appreciate the proof. ;)
So again let's sort it in decreasing order a0 ≥ a1 ≥ ... ≥ an - 1, and we consider the sum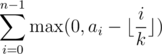 . Now there exists an m such that this sum is equal to
. Now there exists an m such that this sum is equal to  :
: 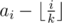 is strictly decreasing as i increases. In other words we can 'assume' that a0 through am - 1 are strictly greater than
is strictly decreasing as i increases. In other words we can 'assume' that a0 through am - 1 are strictly greater than 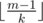 , and the rest at most
, and the rest at most  .
.
To show that this is optimally, let b0, ... , bn - 1 be a permutation of these ai's, and since we spread it over k days, at most k of the coffee cups are the first of the days (hence 0 penalty), at most k of them has penalty 1, and so on. Hence the sum is now at most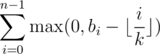 . Choosing only those i's that are relevant, we see that this sum is also equal to
. Choosing only those i's that are relevant, we see that this sum is also equal to  .
.
Now if p is the number of those i's satisfying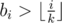 , we can split the sum
, we can split the sum  into two categories: the bi's contain at most m integers from a0, ... , am - 1 and the rest are not more than
into two categories: the bi's contain at most m integers from a0, ... , am - 1 and the rest are not more than  ; so
; so 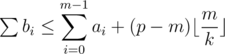 . On the other hand, the sum
. On the other hand, the sum  (considering only those i's that are relevant) at at least
(considering only those i's that are relevant) at at least 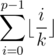 so
so 
Amazing! That's what I was looking for. Thanks.
.
E has another simple solution.
Traverse all pairs in increasing order (starting from (1, 2), (1, 3), ...) and print each pair followed by its flipped pair (not repeating any).
Yeah I also used the same strategy.
i used this too, nice!
There is another solution where in we could start with say pair (1,2) and keep incrementing both the elements of the pair until the second element of the pair reaches k.
After that, we flip the pair and keep decrementing both x and y until y becomes 1. Repeat this process and we get the correct answer.
Yeah ! It is the simplest approach.
Can someone please explain me the tutorial of F1.
It would be of great help.
I solved it in following steps:
Suppose root of the tree is 1.
Then by single dfs we find how many red and blue vertices are present in subtree of each vertex.
Then we see each parent to child edge, if child's subtree contains 0 blue vertices and all red vertices(or 0 red vertices and all blue vertices) then this edge is good.
I think this contest have much tricky questions then previous div3 contest.
the contest was terrible and now seeing from this editorial you really didn't care about us. it's a joke, especially problem D. i'm at a loss of words trying to explain myself why you keep mixing math with programming. what connection do you see between the two? genuinely
In Problem B for n=1 ans should be 0, bcoz if there is only one candy, tanya will give that's one to his father, since now there is no candy she could not eat any day.(There is no candy). Shouldn't it be 0 ? (My soln got hacked just due to only this case which i made myself ans = 0 if n==1) :(
No, because if dad eats the 1-th candy, sum of weights of candies Tanya eats in even days = sum of weights of candies Tanya eats in odd days = 0.
i've learned a lot from this contest, specially that i must read the entire problem set.
Can someone suggest some other approach for F2. Thanks.
Hi, my solution is still similar to the editorial but maybe it can help.
I first run a DFS to do a minimal merge of the components of the same color: I colorize the entire path between each vertex of color, and check for collisions. You only have to keep a count of number of components per color to know if the child has to give its color to his parent.
Then instead of counting the ways of cutting, i count the number of valid colorings, where a color for a node is either "in subtree" or "not in subT". Then for the second DFS I just compute the possibilities for these two "colors". The formulas are similar to editorial.
Solution in O(n log mod) runs in 0.5s, because I took modular inverse to obtain the product of "all but one".
Hope it helps, my code here: 50352250
Could You explain how counting works? I haven't really understood it from the tutorial. Although I understand all the rest.
Either you already have made # of colors in subtree cuts in this subtree or you have made this number minus one. In my case corresponds to "is this node color in the subree?". You can think of DP0 as "am i done here? = has color of parent" so naturally you can keep a color and get from color of child to color of parent but not the converse. Then like classical tree DP you sum possibilities of disjoint events (like choosing one children color) and multiply the ones for independent events (like choosing a color for each subtree). This is not an easy DP pb because you have to keep track of both. Try to get the intuition behind the formulae before looking at tricks for computing it faster.
Okey, I think I am starting to understand it now. One more question. How do we know in our dp that we cut exactly k-1 times? No more no less?
I will try solving some easier problems with tags (trees, combinatorics) and then come back to this one. Thanks
1: you checked there were no collisions during the minimal merging
2: at each cut your separating the "top" color from the "bottom" one, the components stay connected. When you already cut it, a color disappears from the possibilities (DP1->DP0) and becomes a color not in subtree. DP0 means we are done w/ all colors of subtree, DP1 there is one left at the root of subtree.
3: Since you want the root node to have a color from its subtree, you return DP1. Each color except this one has been cut -> K-1.
can anybody take a look to my post here
and help me to optimize my dp solution for the D1 to solve D2
thanks in advance
Its painful to read code of other people sometimes. Let me know if you haven't understood from editorial.
I can’t figure out the counting part. Logic behind dp[v][1] and dp[v][0]
1118D1 — Coffee and Coursework (Easy version)
Let the current number of days be k. The best way to distribute first cups of coffee for each day is to take k maximums in the array
How do you know that it's the best way to distribute? I don't get that
Checking on samples and doing some casework and observations, It is better to use maximum values initially because they may get depleted later on.
Need help with the problem F2. What I've done is-
For every color, tried to build $$$k$$$ same-colored subtrees. If not possible (collision occurs), the answer is trivially $$$0$$$.
For simplicity, let's call uncolored vertices as black vertices. When an answer exists, there will be many (possibly $$$0$$$) subtrees induced by black vertices, whose leaves will have many colored components(sub-trees) adjacent to them. Let's call the set of these colored component/sub-trees $$$S_T$$$ and the black components $$$B_T$$$. Instead of cutting $$$k-1$$$ edges, I tried to color the black vertices in a way such that:
a. only the trees in $$$S_T$$$ get larger
b. no new subtrees form.
c. all the vertices get colored.
Clearly, doing step 2 for all the black sub-trees in $$$B_T$$$ will lead us to the result. The answer will be the product of $$$count(coloring_.a_.black_.component_.in_.B_T)$$$. So, all I need is to find a way to count the colorings of $$$1$$$ black component. It should be an easy DP but somehow I'm failing to grasp it. The tutorial did not help (sorry). Any help is welcome. Thanks.
The way Mike has explained F2 is remarkable. Thanks Mike and Vovuh.
For problem F2 I have an approach. However I am stuck at some part Please read this blog for my approach. Note: For good coders you will find one more interesting problem to solve.