Firstly, huge thanks to Noam527 for guiding me to this solution by providing his output for N = 255. This probably wouldn't have been possible without his help.
As some of you may know, getting 100 points for IOI 2003 Reverse is pretty difficult. The editorial only explains an 88-point solution and there seemed to be no publicly-available code online that scored 100 points when I solved it.
This blog post serves as a tutorial for those who are stuck with 88 points (or less) but who would like 100 points (to fill in that last yellow cell on OIChecklist or just to flex).
88-point solution
I'll just quote the editorial for this.
Consider the case of trying to solve each input with only one
S-operation. Clearly, register 1 might as well as be initialized toN. The register 2 can beN - 2. After printing outN, oneS-operation turns register 1 toN - 1. Register 3 can beN - 5. After printingN - 2,S 3 1makes register 1N - 4. After printing outN - 2,S 1 2turns register 2 intoN - 3, the next value to output. Continuing this through all the registers, 44 is the largest value ofNwhich can be solved in only oneS-operation. This algorithm scores 90% of the points if extended to dealing with multiple operations.
The code for 88 points is pretty clean and elegant. Most people would stop here. However, if you hate yourself want a challenge, then you'd probably try to get 100 points.
100-point solution
The 100-point solution is a relatively simple extension of the 88-point solution.
With the 88-point solution, the only test cases where we won't get AC are the cases with N = 97 (MAX_S = 2) or N > 188 (MAX_S = 4).
Consider the output of the 88-point code for N = 97 (the optimal MAX_S is 2; the MAX_S here is 3):
97 93 86 76 63 47 28 6 0
P 1
S 2 1
S 1 1
S 1 1
P 1
S 2 1
S 1 1
P 1
S 2 1
P 1
S 3 1
S 1 1
S 1 1
P 2
S 1 2
S 2 2
S 2 2
P 2
S 1 2
S 2 2
P 2
S 1 2
P 2
etc.
Notice anything inefficient?
That's right — we can use up to 3 consecutive S-operations but there are many places where we only use 1 or 2 consecutive S-operations. We are effectively wasting S-operations.
Moreover, we can increment any of the 9 values but for each block of consecutive S-operations, we only increase 1.
Here are the first few lines of output for the same case but with the 100-points code:
97 94 89 81 70 56 39 19 0
P 1
S 2 1
S 1 1
P 1
S 2 1
P 1
S 3 1
S 1 1
P 2
S 1 2
S 2 2
P 2
S 1 2
P 2
This is quite similar to the previous output (albeit with only 2 consecutive S-operations instead of 3), but it's the next few lines we should be interested in:
S 4 2
S 2 2
P 1
S 3 1
S 2 2
P 1
Notice how in the 4th and 5th lines, instead of only increasing the value from 1 register, we increase the value from 2 separate registers.
This means that we can waste fewer S-operations! Whereas the 88-point solution would alternate between 1 S-operation and 2 S-operations, the 100-point solution would have sections with only 2 consecutive S-operations, like
S 2 1
S 3 3
P 1
S 4 1
S 1 1
P 2
S 3 2
S 2 2
P 1
S 4 1
S 2 2
P 1
S 2 1
S 1 1
P 4
If we continue this pattern, we notice 2 things:
- The consecutive differences between the starting values of the registers (excluding the first) for an arithmetic sequence of the form $$$3N + 2$$$
- There are 2 types of "cycles" — type 1 is when we "fill in" wasted
S-operations (like above) and type 2 is when we simply follow the strategy of the 88-point solution. We start on a type 2 cycle and whenever we need to print a value that is already present in some register, we switch to the other cycle.
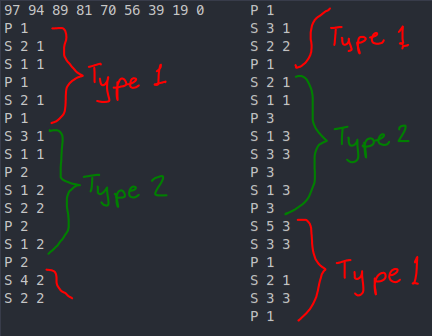
Using this new strategy, we can use only 2 consecutive S-operations for up to N = 101!
It turns out that if we use the arithmetic sequence $$$9N$$$ instead of $$$3N + 2$$$, this strategy also works for 4 consecutive S-operations for up to N = 257.
I found the implementation for this to be quite tricky and I had to use the 88-point code for MAX_S != 2 and MAX_S != 4.
Unfortunately, when I used $$$6N + 1$$$ for the MAX_S = 3 case, it got RTE on some cases. This didn't matter though since the test data was weak enough for a sub-optimal MAX_S = 3 solution to pass. However, I believe it should work for up to N = 179.
If anyone can improve my code or make it more general, please let me know in the comments. Additionally, if anything isn't clear, please let me know so I can try to fix it.











Auto comment: topic has been updated by dolphingarlic (previous revision, new revision, compare).
Hello! I also got a 100 score after 10s of tries.
But I think the limit for $$$N$$$ when $$$s=3$$$ is 173.
Lastly, I think the issue regarding RTE in some cases is the answer you find is better than the solution's answer. After I checked the grader file it had this line
printf("WRONG\nStudent thinks he is better than us.\n");. In my case, because of this reason I got crashed verdict.here is my HUGE CODE https://pastebin.com/Vh8Y5QfL
And we got two more better solutions from int65536 on tests 11 and 14.