DeadlyCritic's blog

Suggestion for testlib's random functions
By DeadlyCritic, history, 4 years ago, In English

In the name of God;

Hi, here I want to suggest some random functions for Testlib.

Testlib has nice random functions, here I want to suggest some other ones. The first and the second random functions are available in testlib, but the rest are not.

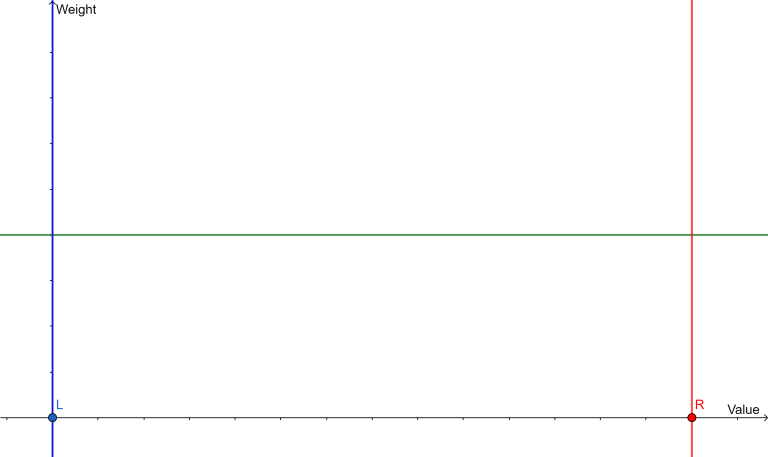
1, $$$\text{rnd.next(l, r)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ with equal weights :

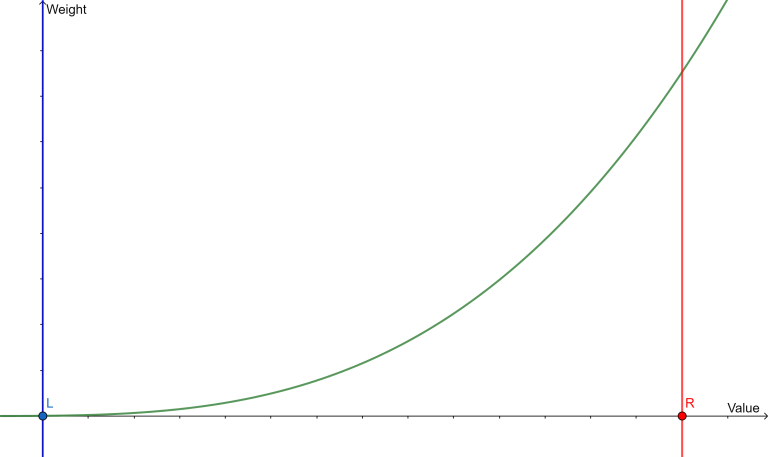
2, $$$\text{rnd.wnext(l, r, w)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ with monotonically increasing/decreasing weights depending on $$$w$$$ :

If $$$w = 0$$$ then it will be equal to $$$\text{rnd.next(l, r)}$$$.

If $$$w > 0$$$ :

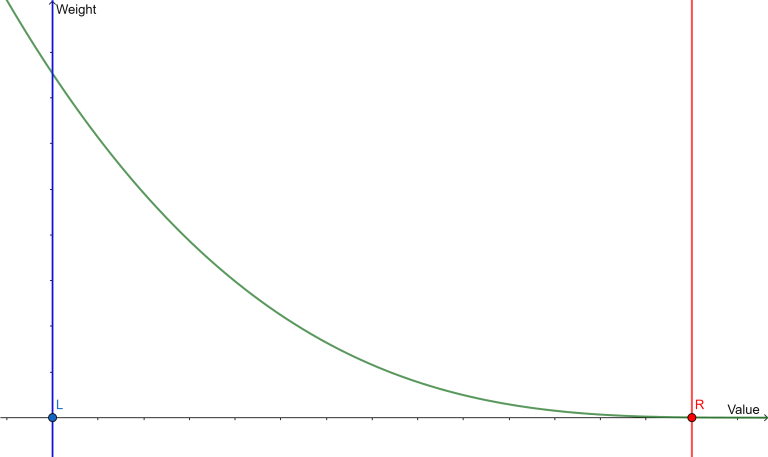
If $$$w < 0$$$ :

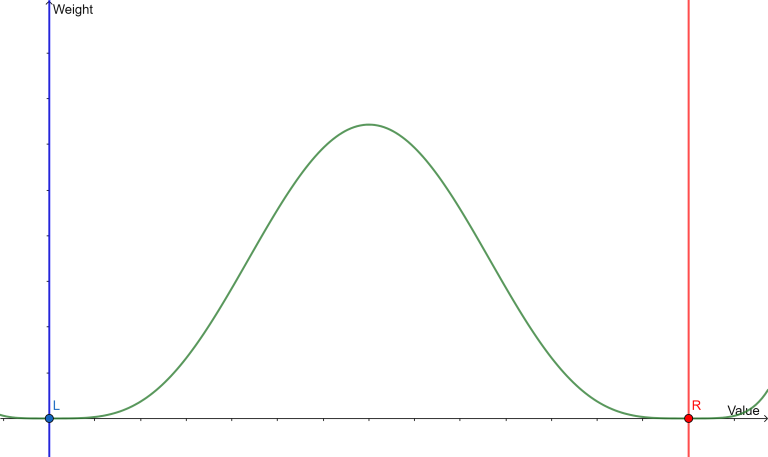
3, $$$\text{rnd.cnext(l, r, c)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ :

If $$$c = 0$$$ then it will be equal to $$$\text{rnd.next(l, r)}$$$

If $$$c > 0$$$ :

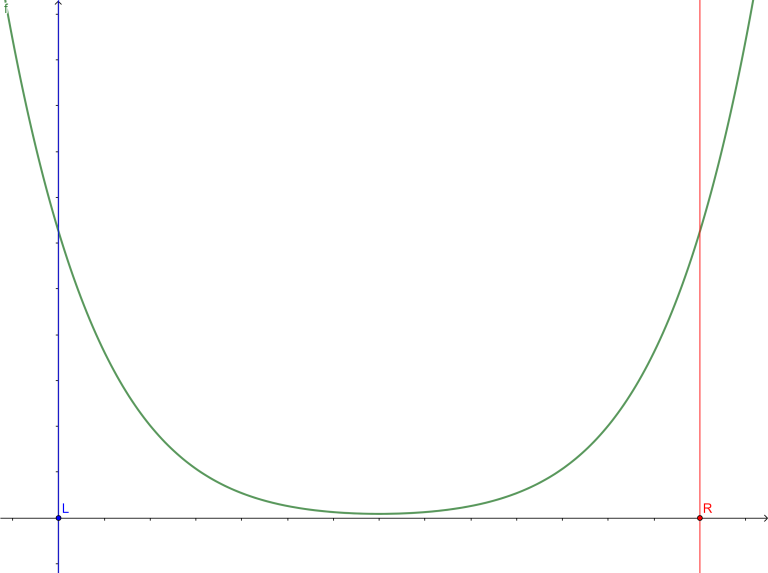
If $$$c < 0$$$ :

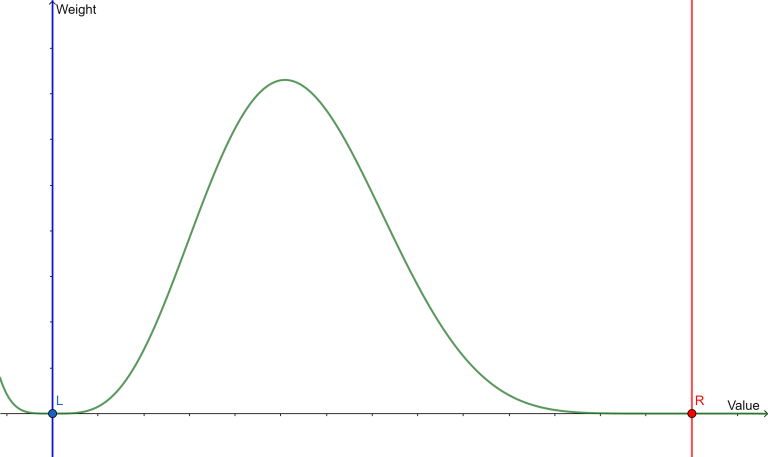
4, $$$\text{rnd.cnext(l, r, c1, c2)}$$$, it will return a random number in range $$$l$$$ to $$$r$$$ like $$$\text{rnd.cnext(l, r, c)}$$$, but its not centered around $$$\frac {r+l} 2$$$ : ($$$c1 \ge 0$$$ and $$$c2 \ge 0$$$)

About the implementation of $$$\text{cnext(l, r, c1, c2)}$$$, its as follow :

  1. Choose $$$c1+c2+1$$$ random numbers in rage $$$l$$$ to $$$r$$$ and sort them.

  2. Return $$$c1+1$$$-th one.

As you can see if $$$c1 = c2$$$ then its equal to $$$\text{cnext(l, r, c1)}$$$.

If $$$c1 = 0$$$ then it will be equal to $$$\text{wnext(l, r, -c2)}$$$, if $$$c2 = 0$$$ then it will be equal to $$$\text{wnext(l, r, c1)}$$$.

Please share your suggestions in the comment section.

  • Vote: I like it
  • +27
  • Vote: I do not like it

»
4 years ago, # |
← Rev. 3   Vote: I like it +8 Vote: I do not like it

$$$\text{cnext(l, r, c)}$$$ for negative $$$c$$$ will be like this :

  1. Return $$$\text{wnext(l, r, 2 ⋅ c + 1)}$$$ or $$$\text{wnext(l, r, -(2 ⋅ c + 1))}$$$ with equal probability.
→ Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

MikeMirzayanov Please add $$$\text{cnext}$$$. Also one can define $$$\text{cnext(l, r, c1, c2)}$$$ for negative $$$c1$$$ and $$$c2$$$, but I didn't add it here.

→ Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

As you can see for an integer $$$x$$$ in range $$$l$$$ to $$$r$$$, the weight of it for different random functions is as follow :

1, $$$\text{wnext(l, r, w)}$$$ :

$$$ \begin{cases} 1, & \text{if $$$w = 0$$$} \\ (x-l+1)^w - (x-1)^w, & \text{if $$$w > 0$$$} \\ (r-x+1)^{-w} - (r-x)^{-w}, & \text{if $$$w < 0$$$} \end{cases} $$$

2, $$$\text{cnext(l, r, c)}$$$ :

$$$ \begin{cases} \text{same as next(l, r)}, & \text{if $$$c = 0$$$} \\ (x-l+1)^c \cdot (r-x+1)^c, & \text{if $$$c > 0$$$} \\ (x-l+1)^{-2 \cdot c + 1} - (x-l)^{-2 \cdot c + 1} + (r-x+1)^{-2 \cdot c + 1} - (r-x)^{-2 \cdot c + 1}, & \text{if $$$c < 0$$$} \end{cases} $$$

3, $$$\text{cnext(l, r, c1, c2)}$$$

$$$ \begin{cases} \text{same as cnext(l, r, c1)}, & \text{if $$$c1 = c2$$$} \\ \text{same as wnext(l, r, c1)}, & \text{if $$$c2 = 0$$$} \\ \text{same as wnext(l, r, -c2)}, & \text{if $$$c1 = 0$$$} \\ (x-l+1)^{c1} \cdot (r-c+1)^{c2}, & \text{if $$$c1 > 0$$$ and $$$c2 > 0$$$} \end{cases} $$$
→ Reply
  • »
    »
    4 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't know how it can be useful for a random person, but no matter what, its beautiful.

    → Reply