Author: PurpleCrayon
Hint
Hint
Hint
Solution
Author: PurpleCrayon
Hint
Hint
Solution
Author: PurpleCrayon
Hint
Hint
Hint
Solution
Author: ijxjdjd
Hint
Hint
Hint
Solution
1540C2 - Converging Array (Hard Version)
Author: ijxjdjd
Hint
Hint
Hint
Hint
Solution
Author: PurpleCrayon
Hint
Hint
Hint
Solution
Author: ijxjdjd
Hint
Hint
Hint
Hint
Solution










PURPLECRAYON ORZ
Damn, so orz round. PurpleCrayon orz
yeah, amazing problemset, not speedforces at all :)
LOL hbarp,even you didn't participate in the contest.
I am curious, how many div2 testers solved D?
like 2 ppl, it was hard for me
Alternate solution to 1540D - Inverse Inversions
(Read the first nontrivial paragraph of the editorial before reading this alternate solution)
Let $$$p_r(k) = x$$$ denote that of the numbers $$$p(1), \ldots, p(r)$$$ in sorted order, $$$p(k)$$$ is equal to the $$$x$$$th of these numbers. We will take a decomposition strategy just as the editorial does, though our strategy will be different. We will divide $$$[1, n]$$$ into blocks of length $$$b$$$. For each block covering some interval $$$[l, r]$$$, we will store $$$p_r(k)$$$ for each $$$k \in [l, r]$$$ in sorted order.
This means that for any $$$k$$$, if we know $$$p_r(k)$$$ for some block $$$[l, r]$$$, then we can determine $$$p_{r'}(k)$$$ for the block $$$[l', r']$$$ immediately to the right by binary searching on the numbers stored for $$$[l', r']$$$. Therefore, we can perform queries in $$$O\left(\frac n b \lg b\right)$$$.
We now need to figure out updates. There are probably simple ways to perform updates in $$$O(b\lg b)$$$, but this yields an overall runtime of $$$O(q\sqrt n \lg n)$$$ which is too slow.
Therefore, we can instead store each block as a segment tree. For each range $$$[l, r]$$$ in the segment tree we store the same thing we store for the whole block: $$$p_r(k)$$$ for each $$$k \in [l, r]$$$ in sorted order.
We then have to quickly merge two intervals. We can merge two intervals of length $$$\lambda$$$ in $$$O(\lambda \lg \lambda)$$$ by doing binary search just as we did above, but this still only yields $$$O(b\lg b)$$$ update overall. However, these $$$\lambda$$$ binary searches can be optimized using two pointers to $$$O(\lambda)$$$, making the overall update $$$O(b)$$$.
We thus have $$$O\left(\frac n b \lg b\right)$$$ query and $$$O(b)$$$ update. Therefore, we can choose $$$b = \sqrt{n\lg n}$$$ to attain an overall runtime of $$$O\left(q\sqrt{n\lg n}\right)$$$ just as the editorial does.
Submission in Kotlin
Submission in C++
It is interesting to note that this solution is quite fast. At the time of writing this update, the C++ version is the fastest correct submission (and runs under 1 second!) and the Kotlin version is faster than the vast majority of submissions.
The 3rd hint for the second problem is same as that of the first problem, is it related or a mistake? UPD: it is corrected.
speedforces.
Problem B Detailed Explanation
Thank you, very well explained
c was too easy, d was too hard. but d was very nice problem though.
Paging ecnerwala to explain his solution to D1E if he'd like. It seems offline?
My solution is $$$O(K N^3 + QN)$$$. I just precomputed the coefficient of each $$$a_i$$$ for each prefix-range for each number of days since person $$$i$$$ becomes positive (only $$$1000$$$ possible days) in $$$O(N \cdot K \cdot N^2)$$$, and then summed up the appropriate ones to answer each query in $$$O(N)$$$. It's written in the offline style to use only $$$O(KN)$$$ memory at a time (grouped by $$$a_i$$$) instead of $$$O(KN^2)$$$.
My passing submission is just $$$KN^3 / 6$$$ instead of the $$$KN^3$$$ I submitted in contest :'(
If you guys wanted to prevent this, $$$K$$$ could've been much higher, like $$$1e18$$$.
:( I knew of this solution (it’s why ML is tight) but I didn’t realize that it could be done offline with small memory. Of course $$$K$$$ higher is obvious solution but main issue is that the extra modulos from binary exponentiation make it very hard to pass in Java without allowing other unoptimal solutions through such as precomputing inverses of the matrix. Probably $$$k=10^5$$$ would’ve been a better choice. Thanks.
Does Div2 D deserved to be D Problem? According to me it should've been Div2 E.
I feel like such an idiot for not being able to understand problem C (Div2). For some reason I thought the nodes were connected like this — 1->2->3->....->N and that we had to minimise answer by adding other edges (of negative weight in case they dont give a negative cycle) to this graph.
But that's exactly what I did, and the final answer is the sum of the array — sum of all subarrays. 120611950
No, that's not what you did. To compute the answer via the method described above, you would have to compute how many elements are lesser than the current element at any given iteration and add them and also keep and their count using a Fenwick tree/ BIT. That's the incorrect approach though because sorting would be more optimal.
Sorry if I misunderstood things. mangat_angad only mentioned adding negative weighed edges to the 1->2->3->...N graph, which is what I thought to arrive at my solution. The array I mentioned is indeed sorted and formed by distance differences which are the weights in the 1->2->3->...N graph. Unfortunately I'm still too noob to understand the tree structures you mentioned.
Nothing unfortunate about it, logic trumps everything
Just want to apologize to authors for the stupidest question, I misread the task..
Can someone tell me the meaning of this line in problem Div2D/Div1B
What same probability are they talking about?
Here's what it's trying to say:
Suppose we start by marking the root. To mark a or b, we must first mark the lca, so we may assume that the lca has just been marked.
And what does this line mean? "The problem can be rephrased as having two stacks of size dist(l,a) and dist(l,b) with an arbitrary p to remove a node from one of the two stack (and 1−2p to nothing) and finding the probability that dist(l,b) reaches zero before dist(l,a)."
Once you've reached the lca $$$l$$$, in a single step you either step closer to $$$a$$$, step closer to $$$b$$$, or step closer to neither.
Can you add implementation for this problem please?
So, we mark lca first (of course). But why wouldn't it affect the final probability of reaching b before a? I mean, why is it sufficient to calculate the probability after marking lca?
Before marking the lca, there is no way to make more progress towards $$$b$$$ than $$$a$$$ or vice versa. The subset of marked vertices also does not change the probability of moving towards $$$a$$$ or $$$b$$$ after reaching the lca because we're choosing uniformly at random and exactly two vertices are of interest.
Now I get it. Thank you.
So, my Solution for Div1 Problem B / Div2 Problem D / 1540B — Tree Array:
Chose two Nodes $$$A$$$ and $$$B$$$ with $$$A>B$$$.
First DFS: Find the path from $$$A$$$ to $$$B$$$. I call it $$$path_p$$$. On $$$path_p$$$ mark the distance to $$$B$$$ for each node.
Second DFS: For each remaining node $$$N$$$ find the shortest path to $$$path_p$$$. It will hit it at some node of the $$$path_p$$$ which has some distance $$$D$$$ marked on it. We mark $$$N$$$ with $$$D$$$. (See comment below for image.)
Calculation: For each node $$$N$$$ we can calculate $$$P_i$$$. $$$P_i$$$ is the probability to reach Node $$$B$$$ before we reach Node $$$A$$$. We sum $$$P_i$$$ for each node. $$$P_i$$$ is also the probability, that the pair of Nodes $$$A$$$ and $$$B$$$ with starting node $$$N$$$ will contribute to the inversion sum.
Iteration: We need to repeat this for each pair $$$A$$$ and $$$B$$$. In the end we divide the answer by $$$n$$$, the amount of nodes (the probability to start with Node $$$N$$$).
This algorithm is $$$O(N^3)$$$. See my Solution 120603369
I wrote myself a small helper DP-program to find the regularities. Let $$$D$$$ be the Distance between $$$A$$$ and $$$B$$$ and $$$d$$$ be the distance from the node $$$N$$$ to $$$B$$$. My educated guess was: $$$P_i=\frac{\sum_{i=0}^{d-1}\binom{D-1}{i} }{2^{D-1}}$$$
It checks for a path of some length for each Intervall $$$[A,B]$$$ which is already visited, what the probability to reach one node before the other is.
Can you explain your solution in a little bit more detail? :')
Oof, I can give you an image, that shows how the distances from the two DFS are distributed on an example. You can see Nodes $$$A$$$ and $$$B$$$ and the numbers are the distances we write into the nodes.
If you have specific questions about some steps go ahead and ask.
what does the dp states mean in your helper program? I am unable to understand. Can you please explain?
You have Nodes $$$1$$$ through $$$N$$$, neighbouring IDs are connected. The state $$$dp[l][r]$$$ is the probability, that node $$$N$$$ will be reached before node $$$1$$$ with all the nodes $$$l$$$ through $$$r$$$ marked already. Obviously $$$dp[1][x]=0$$$ and $$$dp[x][N]=1$$$ ($$$dp[1][N]$$$ can't happen). The recurrence is $$$dp[l][r]=(dp[l-1][r]+dp[l][r+1])/2$$$
I can't grasp the editorial of Div 2 D/ Div 1 B. Can somebody provide a more intuitive explanation?
same :(
Step 1. use linearity of expectation. The answer is
Step 2: Observe that if we start by marking a vertex $$$c$$$ on the path between $$$a$$$ and $$$b$$$, and suppose the next marked vertex on the path is $$$d$$$. Then, the probability that $$$d$$$ is between $$$c$$$ and $$$a$$$ and the probability that $$$d$$$ is between $$$c$$$ and $$$b$$$ are both $$$1/2$$$. This is because there are only two choices for $$$d$$$ and we're choosing uniformly at random. This means that the answer only depends on $$$\text{dist}(c,a)$$$ and $$$\text{dist}(c,b)$$$.
Step 3: run a dp to calculate the probability that we mark $$$b$$$ before $$$a$$$ given $$$\text{dist}(c,a)$$$ and $$$\text{dist}(c,b)$$$.
include<bits/stdc++.h>
using namespace std;
int main(){ ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0); int t; cin >> t; while(t--){ int n; cin >> n; long long arr[n]; for(int i = 0; i < n; i++){ cin >> arr[i]; } long long cnt = 0; for(int i = 0; i < n — 1; i++){ for(int j = arr[i] — 2 — i; j < n; j += arr[i]){ if(j < 0 || j >= n) continue; else{ if((arr[i] * arr[j] == i + j + 2) && (j > i)) cnt++; } } } cout << cnt << "\n"; } return 0; }
/* Accepted code A different approach using arrays (as I don't know what vectors are, haven't read that) I hope this is a optimal approach. Any suggestions related to this are whole-heartedly welcomed. Also, please guide me how could I have optimized the code to a much extent. Thanks in advance! Keep programming! */
.
Not studied yet, I'm still a beginner, but planning to start soon. Thanks for the guidance.
once upon a time, I also did problems while not know what vectors are. sad times :'(
There's no issue in not knowing vectors. Yes they are important I agree but not knowing vectors should not be discouraged. I became expert here without knowing anything about vectors plus he is a beginner so he shouldn't be discouraged like this.
+1, I agree with you. Same I was expert last year solely using arrays
Bas kar bsdk kitna jhooth bolega
Yash.Amin Could you please refrain from using foul language on educational discussions. Thanks
Ah my bad, I did not want to come across as being arrogant, but I was genuinely confused that some people did not know vectors although they are using C++.
Please add implementations too.
Simply running two loops and checking every case would give a TLE. So, we might want to minimize the number of operations. For this, we would only consider the cases where the sum of indices is a multiple of an element.
For this, we would first create two loops, one within the other, first loop iterating i from 0 to (n — 1) with an incrementation of 1. By observation, we can see that the first index for which the sum of indices will be a multiple of arr[i] is (arr[i] — 2 — i).
So, in the nested loop we will run j = (arr[i] — 2 — i) till (n — 1) with an incrementation of arr[i]. We would ignore the cases where j < 0 or j >= n.
Finally, we need to check for how many cases this holds (arr[i] * arr[j] = i + j + 2 and j > i).
Suggestions are welcomed!
include<bits/stdc++.h>
using namespace std;
int main(){
ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int t;
cin >> t;
while(t--){
int n;
long long arr[n];
for(int i = 0; i < n; i++){ cin >> arr[i]; } long long cnt = 0;for(int i = 0; i < n — 1; i++){
for(int j = arr[i] — 2 — i; j < n; j += arr[i]){ if(j < 0 || j >= n) continue; else{ if((arr[i] * arr[j] == i + j + 2) && (j > i)) cnt++; } }}
cout << cnt << "\n";
}
}
/* Accepted code
A different approach using arrays (as I don't know what vectors are, haven't read that)
I hope this is a optimal approach.
Any suggestions related to this are whole-heartedly welcomed.
Also, please guide me how could I have optimized the code to a much extent.
Thanks in advance!
Keep programming!
*/
Use spoilers for writing codes, please!
Actually, this is my first comment. Don't know much of this stuff as of now, but I'll surely take care of it the very next time.
what problem is your code for
NICE CODESTYLE!!!
What is &mdash?
Just curious to know as haven't seen it before.
it is minus (-).
Div2 B can also be done in O(NsqrtN). We know that for a given pair of indeces i+j < 2n, so any pair that a[i] * a[j] < 2n will have to have one of the two terms be <= sqrt(n) (with some off by one errors of course). So the algorithm is to store an array of pairs [array value, index] and sort that array by the value. If the array value is <= sqrt(2n) we can naively loop over the rest of the array in O(n) time and check (be careful about overcount), and if the value is > sqrt(n), we can ignore it. This works since when a[i] * a[j] < 2n one of a[i] or a[j] has to be <= sqrt(2n) and as a result, every pair will be counted.
I don't understand in div1 C why it's prefix of b, in the case i=3 we have $$$a_1+a_2+a_3=f_1+f_1+b_1+f_1+b_1+b_2$$$ so $$$f_1=(ap_i-2b_1-b_2)$$$ I believe the general formula is something in the taste of $$$f_1=(ap_i-ibp_{i-1}+bpt_{i-1})/i$$$ where bpt_i=b_1+2b_2+...+ib_i, I think I miss something
Edit: corrected
Nice problems. thanks for almost fast editorial.
Yes thanks for fast editorial :)
is there anyone who can't even solve one question of today's contest ..
Deleted :)
Please explain div2c/div1a problem a little bit more. Thank you.
Try out this channel
I don't really understand the need for a recursive function for the stack emptying probabilities in 1540B - Tree Array. I mean given that you have a stack of size
nand andmyou can basically have an array of sizen + mfilled with0s and1s where0at theith place means that theith element was taken from the first stack. Any such array which hasn0s andm1s correspond to one process and it's easy to see that whoever takes the last spot in the array gets emptied later which gives an easy way to calculate the probabilities. Namely $$$\binom{n + m - 1}{n - 1} / \binom{n + m}{n}$$$ for the first and similar to the other.If $$$m=2$$$ and $$$n=1$$$, your approach gives $$$\frac{1}{3}$$$. The correct answer should be $$$\frac{1}{4}$$$.
P/S: I'm also curious if there is any combinatoric approach for this,ijxjdjd
I would guess that there’s no easy closed form. You can evaluate in $$$O(n)$$$ however by counting right up paths from $$$(a,0)$$$ to $$$(x,y)$$$ for all $$$a$$$ and multiplying by $$$2^{-steps}$$$.
The problem with this is that all the possibilities are not equilikely, consider $$$m=2, n=1$$$ and let $$$1$$$ denote entries from the stack of size $$$n$$$. Then the probability of obtaining $$$100$$$ is $$$1/2$$$, while obtaining $$$010$$$ and $$$001$$$ has a probability of $$$1/4$$$. Your approach assumes a uniform prior probability (in which case the answer is indeed $$$1/3$$$ whereas here it is $$$1/4$$$ which is the probability of getting $$$001$$$)
Problem Div2C/Div1A, Plz somebody explain 3rd hint. I didn't get why this condition must be true
The sum of the values of edges with positive weight must be ≥ the maximum value in the array.I like to think about C this way: The cheapest node is the root, and the most expensive node, X, is the one with the highest value, D. Therefore no matter how we make our edges, we need at least 1 path from node to X with distance D. So let's build 1 single edge of positive weight from 1 to X with weight D.
Now from node X, all other nodes are <= D. We can use negative edges to go there. Now the problem just becomes "assign as many negative edges as possible" to the rest of the nodes.
In problem 1540B - Tree Array I agree with everything up to:
I agree with this quote if it was about each individual set of marked nodes and single step for them. Because for any individual set of marked nodes, those probabilities is just one over the number of options at the moment. But I don't understand why I should forget about everything else what happens with other parts of tree, because after single step which is neither towards a neither towards b, the number of options (nodes we can mark on next step) may change.
That is correct, but to see how it stays the same you can think of it inductively. Use strong induction and assume probability is the same no matter what the state of the tree is. Then from $$$(x,y)$$$ you always have an equal probability of ending up in one of the two states you can transition to because $$$p$$$ is always the same. Every scenario you enter one state, there’s another scenario with the same probability that enters the other state. So, the probability of entering one of the two states is the same as the other, thus $$$0.5$$$. Hopefully that makes things more clear.
Oh thanks, it's clear now. So, base of induction is when only l reached, and we can show that probability to make step towards a and b is same because for each individual set you can go from l to b instead of going from l into a, using exactly same steps in between (those steps which doesn't change distances to a and b). And similar holds for next steps.
Can you explain this?
Assume $$$X$$$ is initially node we chose. Then define a function $$$g$$$ :
$$$g[a][b][STATE]$$$ = probability to reach a before b while state of the tree we reach is $$$STATE$$$, and $$$a$$$, $$$b$$$ is length of path.
follow the image, I can see : $$$g[a][b][STATE_x] = \frac{1}{4} (g[a][b][STATE_d] + g[a][b][STATE_e] + g[a — 1][b][closer_a] + g[a][b — 1][closer_b])$$$
It can easy see that the probability can change. Or I wrong in some where?
I'll hide my long explanation under spoiler
To put things into words, I want to define some things. First, suppose we marked some $$$s_1, s_2, s_3 ... s_k$$$ vertices in exact this order. Then, let $$$P(s)$$$ to be probability to mark them in this sequence. It can be decomposed into $$$P(s) = p_1 \cdot p_2 \cdot p_3 \cdot ... \cdot p_k$$$ where $$$p_i = 1/o_{i-1}$$$ where $$$o_i$$$ is number of options at step $$$i$$$ — number of opened vertices, except $$$p_0 = 1/n$$$, or $$$o_0 = n$$$.
Then, let $$$l = LCA(a, b)$$$ where $$$LCA$$$ is lowest common ancestor. Then, let $$$x_v$$$ to be some sort of 'cost'. For each $$$v$$$ on path between $$$a$$$ and $$$l$$$ it will be distance to $$$l$$$, and $$$-1$$$ everywhere else. Similarly, for each $$$v$$$ on path between $$$b$$$ and $$$l$$$ let $$$y_v$$$ to be distance to $$$l$$$ and $$$-1$$$ everywhere else. Let
Then $$$A(s)$$$ is equal to how far we reach $$$a$$$, and $$$B(s)$$$ is equal to how far we reach $$$b$$$. Let say we are in situation $$$(A(s), B(s))$$$ after marking $$$s$$$, and therefore situation is pair of numbers. Situation $$$(-1,-1)$$$ corresponds that no vertex is marked on path from $$$a$$$ to $$$b$$$. Situation $$$(0,0)$$$ corresponds to only $$$l$$$ marked on path from $$$a$$$ to $$$b$$$. And situation $$$(1,0)$$$ corresponds to $$$l$$$ and single vertex towards $$$a$$$ is marked.
Finally, let say sequence of marks $$$s$$$ reached state $$$(A(s), B(s))$$$ if either $$$A(s) = x_{s_k}$$$ or $$$B(s) = y_{s_k}$$$, in other words, last vertex is on path from $$$a$$$ to $$$b$$$ and it did change situation.
Now, what we want to prove is following:
For some fixed $$$s_1$$$, which is root we chosen. And the way we prove it is that $$$s$$$ that is reached $$$(\alpha+1,\beta)$$$ consists of $$$u$$$ that reached $$$(\alpha,\beta)$$$ plus additional steps: $$$w$$$ plus $$$s_k$$$. So $$$s = u..w..s_k$$$ where $$$..$$$ is concatenation. It's easy to see what none of vertices from $$$w$$$ is on path from $$$a$$$ to $$$b$$$. Also, it's easy to see that we could instead of choosing $$$s_k$$$ could choose vertex $$$z$$$ towards $$$b$$$, and it would have same probability. In other words $$$P(s) = P(u..w..z)$$$. And this $$$u..w..z$$$ should reach state $$$(\alpha, \beta+1)$$$. So it should be in right side sum of our equation we want to prove.
So, for any $$$s$$$ from left sum, we can make $$$s'$$$ from right sum in unique way, and it will have same $$$P(s) = P(s')$$$. Similarly, for any $$$s$$$ from right sum, we can make $$$s'$$$ from left sum in unique way, and it will have same $$$P(s) = P(s')$$$. So this is bijection, and each element from left sum corresponds to element from right sum with same value, so those sums should have same value. Therefore it's equality.
Initially I wanted to trim $$$s$$$ from $$$(\alpha+1,\beta)$$$ to $$$(\alpha,\beta)$$$ and show similar thing based on following sum:
Which is probability to reach state $$$(\alpha, \beta)$$$, but luckily it didn't required. I'll use notation $$$P(reach(\alpha, \beta))$$$ for this probability.
Thing that is not covered though: why this equality can be translated into probability $$$= 1/2$$$? Well, from $$$(\alpha, \beta)$$$ you eventually will reach either $$$(\alpha+1,\beta)$$$ or $$$(\alpha,\beta+1)$$$, so you can see this as example of Law of total probability. $$$P(reach(\alpha, \beta)) = P(reach (\alpha+1, \beta)) + P(reach (\alpha, \beta+1))$$$, because events $$$(\alpha+1,\beta)$$$ and $$$(\alpha,\beta+1)$$$ are disjoint events given $$$(\alpha, \beta)$$$ is reached. And we proved they have equal probability so $$$P(reach(\alpha, \beta)) = 2\cdot P(reach (\alpha+1, \beta))$$$, so $$$P(reach (\alpha+1, \beta)) = 1/2\cdot P(reach(\alpha, \beta))$$$ which we actually use.
Oh, sorry, there is one missing part. We proved $$$P(reached(\alpha+1,\beta))=P(reached(\alpha,\beta+1))$$$ given $$$(\alpha,\beta)$$$ is reached, but this is actually what we need. This given condition is what I missed. Without given we could reach $$$(\alpha+1,\beta)$$$ from reaching $$$(\alpha+1,\beta-1)$$$.
Thanks for amz explain. I realize that I had some missunderstand in the way we calc $$$P(reach\ A\ before\ B)$$$
This's exactly what in my mind one day ago: let $$$s = ...a...b...$$$ where $$$a$$$ and $$$b$$$ is node $$$a$$$ and node $$$b$$$, "$$$...$$$" mean some node between them which we chose them in exactly that order, or in other word, $$$s$$$ is state represent what we chose (exact in this order) I think $$$P(reach\ A\ before\ B)$$$ (or $$$P(A<B)$$$) must be calculate in this way :
$$$P(A<B) = \sum_{\substack{all\ s\ which\ a<b}} P(s)$$$
But unfortunately, it's wrong (may be, or I still missunderstanding)
$$$P(A) = \sum_{\substack{all\ B[i]\ \subseteq\ A}} P(B[i])$$$ if and only if all $$$B[i]$$$ are distinct
$$$P(A < B)$$$ in your terms is exactly what we need (if a = A and b = B).
I don't understand last formula, everything else looks fine.
And to find $$$P(A < B)$$$ we use fact above and calculate all possible ways to reach $$$a$$$ earlier than $$$b$$$ we use $$$(\alpha, \beta)$$$ states using my notation: you either get $$$\alpha$$$ equal to dist to $$$a$$$ when $$$\beta$$$ = 0, or $$$\beta$$$ = 1, or 2, or 3...
Or you can rephrase task into other task with two kind of balls. What probability to remove all balls of one kind earlier than other, if you pick one or other kind of ball with probability 1/2.
Div2 D, O(N^4) solution 120623566
Your code really helps me a lot in debugging,thanks.
By the way,it's weired that I get Wrong6 when I try to optimize to O(N^3*logN) by binary search on tree.
I have tested my function on other online judge and my function seems to be correct.
Although Div.2 D is harder than ever, in my opinion, it's such a useful and excellent problem.
Is it usual for people to post solutions online during the contest like this channel? https://youtube.com/channel/UCIAiAwwbj9OLmbZehfc28OQ
Can anyone please explain why this submission 120562335 is failing for Div2 B? It would be a great help.
Bro you did not included the condition that i and j should be different i.e (i != j) because it is given in question that no are distinct
I think its covered as I started j from i+1. I tried that explicitly too but it didn't work. I wrote the same idea in a different way and it worked but this kind of implementation is not working.
yeah, you are right, I run your code using vector instead of creating memeset it worked fine, i guess there is some problem in that. 120633207
Only fault in your code is that you didn't used memset correctly
I just changed your memset with this " memset(ind, 0, sizeof(ind)) " and it worked perfectly fine
Thanks a lot to both of you. I shouldn't have used it without properly knowing about it.
Instead of $$$a_i \cdot a_j \leq 2n$$$, we could also check $$$a_i \cdot a_j \leq i+n$$$ which is a bit faster ($$$ \sim 62ms$$$).
can anyone explain B. pleasant pairs more easy words??
And also what is ask in 3rd question i cant understand what asked in it
https://www.youtube.com/watch?v=xCj_ZR5kENo
For those who are searching for a simple solution for great Graphs problems in O (nlogn). https://codeforces.com/contest/1541/submission/120600816
Bro can u explain this soln????? i thought of taking all pairs that give negative edges except for the adjacent pairs.... bt getting wrong ans in 3rd 4th test case.....
while(n>2) { sum-=(n-2)*(llabs(a[j]-a[i])); n--; // n = size i++; // i = 0 j--; // j = n-1 } cout<<sum<<endl;
mysoln
My solution is simple. First sort the array.
Then start connecting adjacent values with their differences. This way sum of all edges with positive weight will be same as the sum of adjacent differences in the array.
After that start making negative edges for every i. So each i will have i negative edges. Where negative weight is same as -(arr[i] — arr[j]).
Instead of search it for every j I have formula as (prefixsum till i) — arr[i]*i
can you tell me why are we sorting the array for a particular node call it x we need to add a negative weight from x to 1 , x to 2 x to 3 till x to x-1 keeping in mind the the path sum doesn't become negative so why are we sorting the array
We are sorting values only once so as to connect neighboring nodes with minimum values,i.e. difference b/w consecutive values.
From this sum of positive edges will be minimum.
ohhh thanks I got it
My solution is working now I only needed to sort the array my code would have been accepted during the contest :(
can anyone explain div2 B plz
here
Beautiful Problems. Amazing Round!!!!
UPD: It's wrong.
For DIV 2C/1A can anyone explain with this test case N = 6 and D = 0 1 2 3 2 3. What are the edges that we can have with their weights?
Hello! The answer would be -18.
Diagram: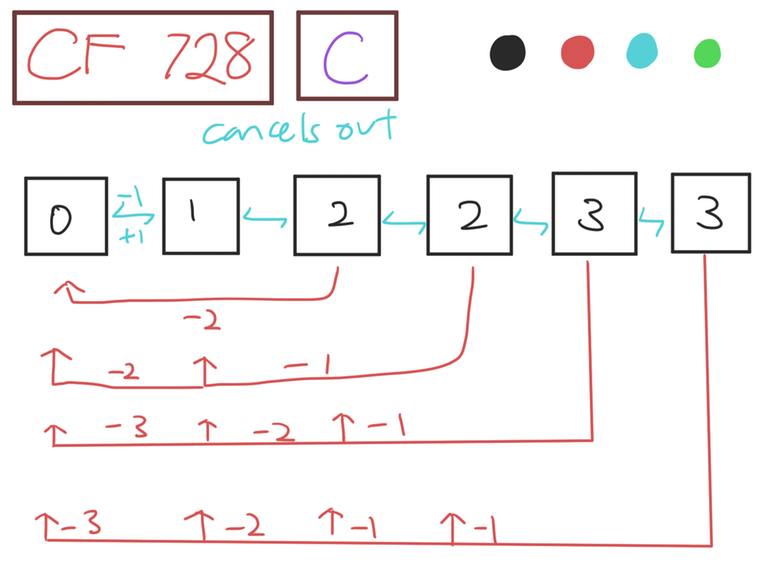
Notice that once you sort the distances, the adjacent nodes have no effect on your final answer. But you can add negative edges as long as they are not adjacent, resulting in such a diagram. Hence you can use prefix sums to solve the problem. (if x nodes came before this, for each node, the answer to add is (x-1)*curr value — csum of first (x-1) nodes).
Hope that made sense!
Thank you Zemrith for so much detail explanation and the solution too it helped me a lot.
first sort the array they will from non negative weight edges. 0 -> 1 -> 2 -> 2 -> 3 -> 3 so the non negative weights will be 1 | 1 | 0 | 1 | 0. form here greedily build most negative weights(backward edges) such that there are no negative cycles.
First you can sort D and get:
N = 6, D = [0, 1, 2, 2, 3, 3]Now calculate the diffs:
diffs = [1, 1, 0, 1, 0]The edges for this graph could be something like this:
Now you have to add more negatives edges, and you could do this by choosing some
iandj,i < jand add an edges fromjtoi, and the weight will be sum of the values fromdiff[i]todiff[j].Another way to think about this is: look at
Darray, it represents distances between adjacent nodes, all we have to do is add all of the edges with length 2, then all of the edges of length 3, ..., all of the edges of lengthN - 1.So, for our case we would have these edges
Thank You ilidar for clearing my doubt and for detailed explaination.
Could someone please provide a more strict intuition or insight of Div2D/Div1B of why "the actual probability p does not matter"? The intuition in the editorial is still alien to me of why those choices of not progess toward to either stacks (and probability 'p' also changes from time to time too) doesn't matter.
Update: Here is the intuition I came up with (The strict proof can be found in the comment of the author below)
Let $$$dp_{i,j}$$$ = the probability of emptying the first stack (which now have $$$i$$$ things left) before the second stack (which now have $$$j$$$ things left) in some states of the current tree.
now, we will try break this $$$dp_{i,j}$$$ down into the sum of $$$dp_{i-1,j}$$$ and $$$dp_{i,j-1}$$$
We will try to illustrate this with trying to split and color, either red or blue, a stick of length $$$1$$$. The length of the sticks representing the 'probability', and the color of the sticks will represent $$$dp_{i-1,j}$$$(red) or $$$dp_{i,j-1}$$$(blue), depending on the color.
Suppose in the current state, we have probability $$$p$$$ for choosing to pop each stacks, and the rest $$$1-2p$$$ of doing nothing. The picture will look like this:
We will split the stick equally(*) into several sticks of length $$$p$$$, and then color two of them red and blue. (* We can split it evenly because in the original problem, $$$p$$$ is in the form $$$\frac{1}{number\ of\ candidate\ unmark\ nodes}$$$ ) Now, the remaining sticks represent the state of $$$dp_{i,j}$$$ again (in some other state of the entire tree, so might be in some different $$$p$$$). That means we will split those sticks similary.
The key observations is:
1) We know that, in the original problem, if we keep picking nodes that aren't progressing toward the target nodes, we will run out of nodes eventually and finally choose the two nodes. That means, all the sticks will eventually colored into 'red' and 'blue'.
2) When we split a stick into several smaller equal length sticks, we will color two of them into red and blue. Those two sticks always have the same length. That means, the total length of blue sticks and the total length of red sticks will be equal in the end.
Analogically, that means, eventually, $$$dp_{i,j}$$$ will split into $$$dp_{i-1,j}$$$ and $$$dp_{i,j-1}$$$ evenly, no matter $$$p$$$ might be or the state of tree of $$$dp_{i,j}$$$ might be. Therefore, $$$dp_{i,j} = \frac{1}{2} \cdot (dp_{i-1,j}+dp_{i,j-1})$$$
Let $$$dp_{i,j}$$$ = the probability of emptying the first stack (which now have $$$i$$$ things left) before the second stack (which now have $$$j$$$ things left), with having arbitary probability $$$0 < p \leq 0.5$$$ of chosing to pick the top of each stack (and $$$1-2p$$$ for doing nothing). Then
$$$dp_{i,j}=\int_{0}^{0.5} x \cdot (dp_{i-1,j}+dp_{i,j-1}) + (1-2x) \cdot dp_{i,j} \,dx$$$
Solving the equation, we get $$$dp_{i,j}=\frac{1}{6} \cdot (dp_{i-1,j}+dp_{i,j-1})$$$ What is the mistake in this logic?
The biggest issue with this logic is that it's assuming $$$p$$$ is arbitrary chosen from a certain state. While $$$p$$$ can be anything in the world, it is always an exact number from a certain state, hence why an integral is wrong.
As a different type of intuition, you can think, "is it more likely to reach $$$(i-1, j)$$$ than state $$$(i, j-1)$$$"? and vice versa. For me at least, I don't see how it's possible for either of those questions to be true, so they should be equal.
If you're looking for a more rigorously correct $$$dp$$$, it would look something like this.
Let $$$dp_{i, j, S}$$$ denote the probability of reaching some node $$$i$$$ distance away before some node $$$j$$$ distance away where $$$S$$$ is a representation of the entire state of of the process (not necessarily an integer). I think you already understood why we can assume the $$$lca$$$ is already reached. We aim to show that $$$S$$$ does not matter in our calculation. Assume inductively that $$$S$$$ does not matter. So, we can assume that states $$$(i-1, j)$$$ and states $$$(i, j-1)$$$ are irrelevant to $$$S$$$. Hence, the part we need to care about is $$$(1-2p) dp_{i, j, S \rightarrow S_a}$$$. A way of thinking about this part of the transition is moving through the collection of $$$S$$$ with the state $$$(i, j)$$$. Obviously, the $$$dp$$$ is a $$$DAG$$$ because no state $$$S$$$ can reach another. Each bounce takes a certain probability $$$p$$$ which is just multiplied in the current path. So, for each state $$$S$$$ with state $$$(i, j)$$$, we have a certain probability to reach it by simply calculating $$$dp$$$ along a DAG as is traditional. Then, from those states of $$$(i, j)$$$ you transition to $$$(i, j-1)$$$ with an equal probability $$$(i-1, j)$$$. So, they have to be equal. Finally, this argument holds for any initial state $$$S$$$ that you reach, so we can conclude that, from any state $$$S$$$ with a state of $$$(i, j)$$$, the probability of transitions to $$$(i-1, j)$$$ and $$$(i, j-1)$$$ are always exactly $$$0.5$$$.
I see, thank you so much!
I am getting wrong ans . could someone tell me where the code make differene ( [yestrday competiton problem .
`](https://codeforces.com/contest/1541/problem/B).
v[i].first * v[j].first can create overflow. So, you need to convert them to long long by using
ll left = 1LL * v[i].first * v[j].first;
instead and it would pass.
(Simply save the value in long long won't help. You need to convert them to long long before doing multiplication. 1LL* is one way)
Hi, in problem Div1.B/Div2.D; I can't wrap my head around $$$F[x][y]=F[x−1][y]/2+F[x][y−1]/2$$$. Why is it not $$$F[x][y]=F[x−1][y+1]/2+F[x+1][y−1]/2$$$, can someone please explain to me why is my transition wrong and/or why is the aforementioned transition correct?
x and y is the distance left for each side right? So, if you take one out, it won't make sense to add that one to the other side since the distance should be either x-1 and y or x and y-1.
Thank you so much I understand. I had a minor misunderstanding of the parameters to the dp state.
PLease explain why 2 same codes are not giving the same ans
code forces round 728 div2
Problem B :https://codeforces.com/contest/1541/problem/B
AC Submission : https://ide.codingblocks.com/s/579769
Wrong output Submission :https://ide.codingblocks.com/s/579771
Difference is using of macro (node) instead of pair<int,int>
Please help
If i am using #define node pair<int,int> it is getting accepted but when i am using typedef pair<int,int> node; it is giving wrong answer
Why this is happening ?? Is it a bug??
Not really sure why this is happening.
However, I think the problem is the position of #define int long long. So, for #define pair<int,int> node it seems that compiler change node -> pair<int,int> -> pair<long long, long long>. However, when you do typedef, it still keeps in pair<int, int> which creates an overflow problem later on.
I did try moving #define int long long up above typedef and the code pass. So, my best guess is #define int long long only replace int after that position with long long. Thus, node is still pair<int, int> in the typedef solution, while node is changed to pair<long long, long long> in the second solution.
May I ask why in the Div1D solution ci=i-bi, I think it should be ci=bi ...
Check the definition of bi again dude. bi here means number of elements greater than pi. So to get ci, which is number of elements smaller than pi, you need i-bi.
I read it again. If I read it correctly, bi stands for j<i,pj>pi, and ci stands for j>i,pj<pi. For example, p={1,3,5,4,6,2}, I think b4=1,c4=1, please point out my problem
oh, the array index starts from 1
You are right.
I guess it might just be typo and ci stands for j<i, pj<pi. At least with this definition of ci the algorithm seems correct :)
thanks!
Here's my solution of B div 1 / D div 2 without LCA, using single DFS per node. 120700765 It is similar to what OleschY suggested above. I've tried to describe it in the blog
Can someone explain how you can find the LCA for each pair so quick? Iterating through every root is and then considering every pair is already N^3
There are a couple ways you could do it:
Thank you so much for the detailed answer!
O(n2) is also working for div2 C Great Graphs. https://codeforces.com/contest/1540/submission/120964787
Div1D can be done in $$$O(n \sqrt{n})$$$. We can use square root decomposition to replace all BITs in tutorial. Since a value in a non-updated position changes by at most one and all values change in the same direction, the full recomputation is only needed in the updated position and we can perform an incremental change in $$$O(1)$$$ for values in each non-updated positions.
Code
Realy impressive solution. I'm surprised no stars were given to you until me. Maybe many people didn't get your idea since the solution is actually much more complicated than your brief comment(at least in my opinion). I also wrote a piece of code which used your method but simplified a small part of steps. Here it is.
ijxjdjd in problem Tree array you said that Fixing a given root r, the expected value of the entire process is obviously the sum of the expected values for a fixed root divided by n.
why we divide by n at the end ?
The calculation is independent based on whichever node that you choose first (it becomes the “root”). Initially you choose one of $$$n$$$ nodes with equal probability so you divide by $$$n$$$ at the end after you’ve summed up the independent expected value after choosing the node $$$i$$$ initially.