363A - Soroban
Not so much to say about this problem. You need to extract the digits of the given number (read it as string or repeteadly divide by 10 and take the remainders). Then carefully do the mapping of digits to its' representation.
363B - Fence
Another easy problem. We need to calculate the sum of every consequtive segment of k planks. One way to do this is to calculate partial prefix sums: 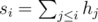 . Then the sum of heights of the planks i, i + 1, ..., i + k - 1 is si + k - 1 - si - 1. The other approach is to calculate the sum of the first k planks: h1 + h2 + ... + hk. By subtracting h1 and adding hk + 1 we get sum of k planks starting from the second plank. Then, by subtracting h2 and adding hk + 2 we get sum of k planks starting from the third plank, and so on.
. Then the sum of heights of the planks i, i + 1, ..., i + k - 1 is si + k - 1 - si - 1. The other approach is to calculate the sum of the first k planks: h1 + h2 + ... + hk. By subtracting h1 and adding hk + 1 we get sum of k planks starting from the second plank. Then, by subtracting h2 and adding hk + 2 we get sum of k planks starting from the third plank, and so on.
363C - Fixing Typos
The general idea of the solution is the following: while there are three consequtive equal characters, remove any one of them. After that we can only have typos of the second type. So, if we have one couple of equal characters immediately after another couple of equal characters (xxyy), we need to decide which character to remove, x or y? Let's find the leftmost typo of the second type in the string. It is easy to see that we can always remove the character from the second couple.
All these can be done in a single pass. Go through the characters of the given string and build the resulting string ans. Let's denote the current character as ch. If ch is equal to the last two characters of ans, skip ch. If ch is equal to the last character of ans and ans[length(ans) - 2] = ans[length(ans) - 3] (assume that ans is 1-indexed), skip ch. Otherwise, append ch to ans.
363D - Renting Bikes
Let's do a binary search over the number of boys that can rent a bike. So let's say that we want to check whether it possible for k boys to rent bikes. If some k boys can rent a bike, then the k "richest" boys (with the most amount of personal money) also can do that. It is easy to see that if they can rent bikes, they can rent k cheapest bikes (if we first sort the bikes in increasing order of price, it will be just the first k bikes).
So, take k richest boys and try to match them with k cheapest bikes, spending as much common budget as possible. The following algorithm works (try to understand and prove it before asking questions): take the boy with least number of money (of course, among the considered k richest) and try to give him the cheapest bike. If the boy has ehough personal money to rent this bike, use his money to do this. Otherwise, use all his money and take some money from the common budget. Continue this process with the second cheapest bike and the second "poorest among the richest" boys. This process can end in two ways: we will either run out of budget and fail to rent k bikes, or we will successfully rent these bikes.
363E - Two Circles
Correct solution will be published later.











It's Amazing to see tutorial of CF round #211 before round #210
Could you please send me the standard solution for problem E?
I have some wonder on the correctness of the solution. ( See this post: http://codeforces.com/blog/entry/9538 )
thank you.
the fact that the length of tutorial for problem E exceeds the sum of lengths of the other four problems suggests how difficult it is :P
EDIT: tutorial for problem E has been removed now! i wonder why, as very few coders solved it during the contest!
Hi, anyone can tell me why i got WA in this submission for problem C? 5069514
The problem is in your code (string ret have length 3 instead of 2) see this submission 5069697
You also output
'\0', it's a well-known bug of grey and green codersProblem E is Knapsack problem?
O_o No way, it's some sort of precomputation-geometry stuff. Not sure what exactly, it's ugly.
For each circle, compute the sum of its cells. Then we fix one circle
(x1, y1)and try to find the maximum possible other one(x2, y2).Notice that because the radius is fixed, we can easily precompute for every value of x1 — x2 what is the maximum value of k such that we can't place the second circle on the segment from
(x2, y1 - k)to(x2, y1 + k). So we only need to loop for every value of x2 and get the maximum of all circle from(x2, r + 1 ... y1 - 1 - k)and(x2, y1 + 1 + k ... n - r). This can also be precomputed.Total time complexity is O(N^3)
I thought of 2D segment tree and gave up :((
I precalced all circle sums: Calculate sum of first circle in O(R²), calculate sum of other O(N²) circles in time O(R) (use sum of adjacent circle and update border). O(N*N*R)
Then, for each row: For the first cell, create a map (circle sum => count), which counts occurrences of circle sums in the whole field excluding circle sums of colliding circles in O(N²). We can pair the circle at the current position with K other circles with a total of (sum of current circle) + V, where V is the biggest V in the map (V=>K). Update end result accordingly. For the other O(N) cells, update the map in O(R) (and update the end result). For all rows this is: O(N * (N*N*logN + N*R*logN))
This results in O(N*N*N * log(N)).
At first I ran into the time limit. I speed up my solution by skipping circle sums for the map that are obviously irrelevant (smaller than: best sum of two circles (so far) — maximum of a circle sum in the current row).
In solution to D, you are actually maximizing the number of children who can rent a bike. For this you are doing a binary search on the number of possible answer (i.e. from 0 to m).
But there is another secondary condition which needs to be fullfiled and that is minimizing the personal amount. Taking k richest boys can satisfy to buy maximum k cheapest bikes but it may not be the minimized personal amount spent. There can be some shared amount left in renting k bikes and hence another boy (not in the k top richest boys) can be able to rent this buy with lesser personal amount.
Let me know if i am missing anything.
Actually, choosing k richest boys and k cheapest bikes is just to check if it is possible to rent k bikes. Once it is possible to do so, we simply spend all of the shared budget renting k bikes (min(shared budget, total costs of k bikes)) to minimize the personal amount. It doesn't matter which boys are chosen in this case.
can someone explain the proof of greedy property form problem D? :D Thanks in advance
I do not know how to formally prove it but here's my best to explain my thought:
assume we have sorted boys money in A[], sorted bikes price in B[];
assume we have fix k boys
a_1, a_2 ... a_kand k bikesb_1, b_2...b_kanda_i boy buys b_i bikeI want to check if any other scheme will make me use less share money (as it can potentially make more boys buy bikes)
Let's pick any a_i,a_j and b_i, b_j where i < j,
try to swap them to see if we can use less share money
i.e. a_i buy b_j and a_j buy b_i
Case 1: if b_i <= a_i, then a_i, a_j >= b_i,it is always better using a_j buy b_j as a_i can afford b_i by himself --> No swappingCase 2: if b_i > a_i,no matter b_i > a_j or b_i <= a_j, swapping them won't able to make result better --> No swappingSo using this greedy scheme to buy the bikes uses least share money for a fixed k boys and k bikes.
Then, obviously for a fix k after bsearch, we can, again,
greedily choose the richest k boys to buy the cheapest k bikes as they should make us possibly save more share money
Lastly, when we know how many bikes k we can buy, we do not need to know which k boys buy them, as the total minimum answer is always the cheapest k bikes minus all share gold
" You are allowed to delete letters from both ends and from the middle of the word."
so why are we deleting from anywhere in string?
Even I'm confused with the problem statement. I think the problem setter intended to say "You are allowed to delete any character from the word, including characters at both ends."
I have a test case for 211 div2 D problem? suppose following is the test case:
Then what should be the output? I think it is "3 10" . Because 1st bike can be bought with personal 4 rubles from 1st person,2nd bike can be bought with personal 3 rubles from 2nd person,3rd bike can be bought with 4 rubles from 3rd person.With the shared money it is always possible. But in the AC solution it gives output as "3 14". Any help??
In the task it is said that we need to output the minimum amount of personal money spent, not common.
What is the meaning of the statement "You are allowed to delete letters from both ends and from the middle of the word" in the question FIXING TYPOS. I thought we could only delete an element at the beginning, or at end or in the middle at once.
exactly !! like for a test case "abcdefgghhi" output should have been "abcdefggh" with length 9 but according to the tutorial given its "abcdefgghi" with length 10 ! I used recursion for the deleting condition as given in question but its giving TLE for testcase 5.
Can anyone help me with this test case of problem B Fence? I can't figure out what is going wrong here . Submission link: https://codeforces.com/problemset/submission/363/110904366
update your sum, everytime you move out from block.
oh right. Got it . Thank you very much