369A - Valera and Plates
We will use greedy algorithm. Let's now i-th day, and current dish is a dish of first type. Then if we have the bowl, let's use it. Otherwise we will increase the answer. If the current dish is a dish of the second type, we first try to get the plate, and then the bowl. If there are no plates/bowls at all, then we will increase the answer.
Author's solution: 5306397
369B - Valera and Contest
In this task you are to determine such array a1, a2, ..., an, that following conditions are met:
- r ≥ a1 ≥ a2 ≥ ... ≥ an ≥ l;
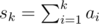 ;
;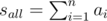 ;
;
It's clear to understand, that value sk should be distributed evenly between the first k elements. For example, you can use following algorithm:
remainder = (s_k mod k);
for(int i = 0; i < k; i++)
{
a_i = s_k / k + (remainder > 0);
remainder = remainder - 1;
}
If k ≠ n, you should use same algorithm with other elements, but there are to distribute value sall - sk.
Some participants forgot about test, where k = n. They received RE11.
Author's solution: 5306414
369C - Valera and Elections
Consider all the roads that we need to repair. Mark the ends of u, v white. After that, we will consider a simple dynamic programming d[v] (v is the vertex) on the tree that for each vertex in the tree determines the number of white vertexes in the subtree. It is easy to calculate this by using a recursive function calc(v, prev) (v is the current node, and prev its immediate ancestor):
calc(v, prev)
{
d[v] = 0;
if (white[v])
dv += 1;
for all vertexes u such that there is the edge (u,v) or (v,u), u != prev:
calc(u, v);
d[v] += d[u];
}
After that we will add to answer all white vertexes v such that next condition is correct: d[v] = 1
Author's solution: 5306500
369D - Valera and Fools
Let's p[A] is the pA from the statement.
It's clear to understand that you can discribe the state by using pair of integers (A, B), where A is a number of the fool with smallest index, B — the second fool from the left. It is clear to understand that fool with indexes j ≥ B will be living. After that we will use bfs on the states (A, B).
State (0, 1) is always visitable, because it is initial. We will push it in the queue. After that, there are only three transitions from current state (A, B).
- (B + 1, B + 2) — this transition is possible if and only if p[A] > 0 and there are some fool with index j ≥ B, which has non-zero value p[j] > 0.
- (A, B + 1) — this transition is possible if and only if p[A] > 0 и there are no fool with index j ≥ B, which has p[j] = 100.
- (B, B + 1) — this transition is possible if and only if p[A] ≠ 100 and there are some fool with index j ≥ B, which has non-zero value p[j] > 0.
After that you are to determine number of states, which has distance from state (0, 1) less or equal to k. Also you should be careful, that if there are only one fool, that he doesn't shot.
Author's solution: 5306516
369E - Valera and Queries
Let's calculate sets xs[y] — all segments, whose right borders are exactly equal to y. Now we reduce our task to another. For each query we will count the number of segments that doesn't belong to any one point. Let's it will be the value v. Then the answer to the query is n - v. We add to our request the point 0 and a point MV + 1, where MV = 1000000. Let points request have the form x1 < x2... < xn. Consider the xi and xi + 1. Let pi is the number of segments that lie strictly inside xi and xi + 1. Then v = p1 + p2 + ... + pn - 1. We will use following algorithm to find the values pi. Let consider all such pairs (x, xi + 1) for all requests and to add them to a second set xQ[y] — all pairs whose right boundary is equal to r. Then to find the values p of pairs (xi, xi + 1) we will iterate ascending the right border. Additionally, we will support Fenwick's tree, which can make + = 1 at the point, and can calculate sum of the prefix. Let i — the current right border. Then we can find out the value p for all pairs (l, r), with the right border is equal to the i (l, i). Let j left border of the pair. Then the answer for the pair is the value of S - sum(j), where S — all added to the Fenwick's left borders, and sum(j) — sum of the prefix j. After that, for the current coordinate i we need to consider all segments in the set xs[i]. Let j left boundary of the segment. Then we need to make + = 1 at the point j in our Fenwick's tree. The total solution complexity is 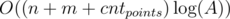 .
.
Authors solution: 5306535











random_shuffle(ans.begin(), ans.end());dafuk :D
Isn't that Bogosort?
One iteration of Bogosort.
Redundant Input in "B" confused me :(
PRoblem D what is the Difrrence Between Using BFS and Using Recursion at the same code here ?! bfs get AC and recursion get WA !!! http://ideone.com/WpPgn1
BFS gives you the shortest path, while DFS (recursion) just tells you whether or not a path exists.
in this problem the path length is important because you want all states within a distance of
kfrom the start state. therefore DFS would not be a right solution.Hello guys,
I need a little help with the Varela and Fools problem.
Can you see my submission? When I compile and test with the first test case (on my machine, using g++), i get 7 as answer (correct answer), but the judge is saying that my code gives 4 as answer.
What can I do? http://codeforces.com/contest/369/submission/5324049
If you compile it with -pedantic flag it says something like
warning: ISO C++ forbids variable length array ‘p’So instead ofp[n]you should do something likep[3000].for problem D, each currently living fool shoots at another living fool with the smallest number (a fool is not stupid enough to shoot at himself). So the smallest number shoots whom? randomly or just the fool next to him? I think it is not clear. thanks
ah got it, thanks and sorry.
In Problem E solution i didn't understand the algorithm which calculates the value of pi, any help ?
Getting "Memory Limit Exceeded" in C. Please help
29529634
I am Using DFS, once a bad row is encountered say v->v+1, the program saves the corresponding leaf l in a set(by going deeper and deeper till leaf is encountered), this way all the bad roads from v+1 to l are also repaired.
you may have got
stack overflowduring recursion. I have gotMemory limit exceeded on test 6before:32189259.After purning inefficient dfs steps, I got
Accepted. just like this:32189351.60057569 is giving MLE, unable to figure out what to change.
I am also getting Memory Limit exceeded on test 6 260674620 could you help me figuring out this? and what steps have you taken?
For B, why don't we need to use l and r (the lower and upper limits)?
Can somebody share some different approach for C — Valera and Elections?
Let's call edge with 2 "Problem edge"
If any node having a Problem edge between it's parent and the subtree of that node doesn't have any Problem edge then this node must be included in the answer.
This can be solved using simple DFS.
refer this