Considering all the color revolutions my last blue point was after Codeforces Beta Round 62
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |
I like to build my cp library. I am not aiming to fill it by each algo I have met, so content looks poor. Instead I am focusing on frequently used features or implement convenient api for powerful methods.
Also I like to rate cp libraries of others and currently I noticed that my lib have enough implementations which I never seen before, so I want to share it with community.
Hope it will inspire you to improve or rewrite your library and eventually rethink about some algorithms (which happens to me couple times).
#5 Centroid decomposition
graphs/trees/centriod_decomposition.cpp
This one is the perfect example of what I am calling convenient api. I've seen a lot of centroid decomposition snippets and almost all of them is template code or unfinished data structure with piece of code where you need to add your solution. I have snippet that doesn't need changes at all and I need to just call it.
centriod_decomposition(tree, [&](auto &g, size_t centroid, size_t sizeof_subtree) {
//g - is current subtree and I can freely traverse it from centroid by dfs
});
Once I've seen almost similar implementation but author passed to lambda original tree and vector of blocked vertices. I feel this uncomfortable to code: you still need to take in mind that vertex can be inaccessible.
It has little overhead from coping graph but I have never stubbed on this because overall running time is more crucial.
#4 Parallel binary search
misc/parallel_binary_search.cpp
Well, it is actually not general (can't solve this) but I am working on this. This one about "find first version of data where query is satisfied".
It rarely used but api is really sweet. Here I need to describe scope where I set predicate, implement evolution of data and just commit all changes — internally all queries will be executed in necessary moments.
auto res_bs = parallel_binary_search(qn, m, [&](auto vc) {
//usually create init data
vc.pred = [&](size_t qi) {
//check query in data and return true/false
};
//do changes of data and call vc.commit() on each
});
Some examples:
auto res_bs = parallel_binary_search(qn, m, [&](auto vc) {
dsu g(n);
vc.pred = [&](size_t qi) {
auto [x, y, z] = queries[qi];
if(g[x] == g[y]) return g.size(x) < z;
return g.size(x) + g.size(y) < z;
};
for(auto [i, j] : edges) {
g.unite(i, j);
vc.commit();
}
});
auto res_bs = parallel_binary_search(qn, n, [&](auto vc) {
aggregator<node> t(n);
vc.pred = [&](int qi) {
auto [ql, qr, w] = queries[qi];
return t(ql, qr).seg < w;
};
for(auto [_, i] : pa) {
t.set_value(i, 1);
vc.commit();
}
});
full code: 188125552
As bonus this implementation has very low time and memory overhead. It not uses map or vector of vectors: you can store all unfinished ranges sorted by left and very easy to split it to new groups in place.
#3 ilist<T>
Implicit splay tree with iterators (stl style). It has api close to std::vector and not invalidating iterators like in std::set.
ilist<int> a;
a.push_back(0);
a[0] = 10; //O(logn) access
a.assign(begin(vec), end(vec));
for(int &x : a) ++x; //traverse from begin to end
while(std::size(a) < 10) { //calls a.size()
a.insert(begin(a), 1); //O(logn) insertion
}
ilist<int> b = a; //makes copy
a.insert(begin(a), b.extract(begin(b) + 3, begin(b) + 6)); //O(logn) cut
a.insert(end(a), std::move(b)); //moving without coping
auto it = a.at(5); //iterator to 5th item
assert(begin(a) + 5 == it); //iterator advance in O(logn)
assert(it - begin(a) == 5); //iterators distance in O(logn)
assert(std::next(it) - begin(a) == 6); //also has ++it
assert(std::prev(it) - begin(a) == 4); //and --it
This snippet is biggest one but is not in final state. As TODO I want to implement reversible option and build link-cut trees that use it as black box.
#2 NTT (with modulos calculated in compile time)
My ntt is very default and maybe slow but it have no hardcoded ntt-frendly modulos. Actually I can understand why you add 3-5 modulos in ntt snippet but what I do not is hardcoding attendant stuff for it like roots. Seriously all this can be calculated in runtime easily. But with power of c++ all modulos can be calculated too!
As result convolution receives parameters and compiler will generate modulos that satisfy them.
convolution<modint<998244353>>(a, b); //will recognise as ntt-mod
convolution<modint<786433>>(a, b); //same! check codeforces.com/gym/100341/problem/C
convolution<modint<1000000007>>(a, b); //will generate 3 modulos and combine result by CRT
convolution<uint64_t, 1<<20 ,5>(a, b); //will generate 5 modulos good for length at most 2**20
#1 Hashing
And finally my favorite... strings/hasher.cpp
My hashing snippet uses famous rolling hash with $$$mod = 2^{61}-1$$$ with magic bit multiplication which works really fast.
Lets define core usual primitives about hashing and just implement it:
hash_t — wrapper of uint64_t containing raw hash (special case of modint)
hashed — what remains from string after it... hashed: hash_t and its length
hashed h = str; //from std::string
h.length() // length of hashed string
if(h1 == h2) // equality check in O(1)
h = h1 + h2; // concatenations in O(1)
h += 'a';
hasher — hash array of string/vector, allows get hash on range in O(1)
hash_span — reference to some range in hasher
hasher a(str), arev(rbegin(str), rend(str));
a.substr(start, length); // hashed
a.subhash(start, length); // hash_t
hash_span s = a(l, r);
assert(s.length() == r - l);
assert(a[s.start()] == s[0]);
hash_span also have overloaded operator< (in $$$O(\log len)$$$) which can be used in std::sort or std::lower_bound.
Looking at language statistics in last rounds I have wondered why so many Java and so extremely low Kotlin coders?
| GNU C++ | 16071 |
| Python 3 | 1121 |
| Java | 708 |
| GNU C11 | 177 |
| MS C++ 2017 | 139 |
| C# | 23 |
| Kotlin | 13 |
| Rust 2021 | 6 |
| GNU C++ | 13731 |
| Python 3 | 825 |
| Java | 518 |
| GNU C11 | 131 |
| MS C++ 2017 | 90 |
| C# | 13 |
| Kotlin | 9 |
| Rust 2021 | 6 |
| GNU C++ | 11739 |
| Python 3 | 812 |
| Java | 422 |
| MS C++ 2017 | 78 |
| GNU C11 | 68 |
| C# | 12 |
| Rust 2021 | 10 |
| Kotlin | 9 |
Kotlin, in a rough sense, is modern replace for Java, so...
If you are Java-coder then I am curious why you not change Java to Kotlin?
I don't want to note basic advantages of Kotlin which described everywhere. But it is language with modern syntax, and I think it is cool for cp almost as Python. I have more than one year experience of coding in Kotlin (but not cp!!), and I can describe my feelings as "I will never write even single line again in Java".
Maybe you remembered Kotlin as not so cool language when it was 1.4 but now (1.7 in moment of writing this blog) both syntax and std lib have improvements. For example, instead of readLine()!! now it is readln(). Or modulo function
val MOD = (1e9 + 7).toInt()
println((-1).mod(MOD)) //1000000006
println(((MOD-1L)*(MOD-2L)).mod(MOD)) //2
Usage of lambdas in Kotlin is awesome. Just look at this custom comparator:
data class Segment(val l: Int, val r: Int, val id: Int)
...
segments.sortWith(compareBy<Segment> { it.l }
.thenByDescending { it.r }
.thenBy { a[it.id] }
)
Last what I really like is extensions, great for templates/libraries
fun IntRange.firstFalse(pred: (Int) -> Boolean): Int {
var l = first
var r = last + 1
while (l < r) {
val m = (l + r) / 2
if (pred(m)) l = m + 1 else r = m
}
return r
}
//usage:
val i = (0 .. 2e9.toInt()).firstFalse {
1L * it * it <= s
}
TL;DR: range_sum_range_add with only two BITs.
Suppose we have (sub)task to proceed following queries:
range_sum(l, r)range_add(l, r, x)
Most familiar solution is segment tree with lazy propagation. And maybe you didn't knew, but such segment tree does not needs pushes!
template<class T>
struct rsq_add_segt {
explicit rsq_add_segt(size_t sz = 0, const T &val = 0) {
for(d=1; d<sz; d<<=1);
t.assign(d*2, {val, {}});
}
rsq_add_segt(const vector<auto> &vals): rsq_add_segt(size(vals)) {
for(size_t i=0; i<size(vals); ++i) t[i+d].first = vals[i];
for(size_t i=d; i-->1; ) t[i].first = t[i*2].first + t[i*2+1].first;
}
void add(size_t l, size_t r, const T &val) {
if(l>=r) return ;
_add(l, r, val, 0, d, 1);
}
T operator()(size_t l, size_t r) const {
if(l>=r) return {};
return _calc(l, r, 0, d, 1);
}
private:
size_t d;
//t[i] = pair of #(sum on range of node) and #(total additions on range of node)
vector<pair<T,T>> t;
void _add(size_t i, size_t j, const T &val, size_t l, size_t r, size_t v) {
//adding to whole range
if(i==l && j==r){
//sum increases by value * length_of_range
t[v].first+=val*T(r-l);
//total addition increases by value
t[v].second+=val;
return ;
}
size_t m = (l+r)>>1;
if(i<m) _add(i,min(j,m),val,l,m,v*2);
if(m<j) _add(max(i,m),j,val,m,r,v*2+1);
//update current node: sum on range is sum of children + own addition
t[v].first = t[v*2].first + t[v*2+1].first + t[v].second * T(r-l);
}
T _calc(size_t i, size_t j, size_t l, size_t r, size_t v) const {
//sum of whole range already known
if(i==l && j==r) return t[v].first;
size_t m = (l+r)>>1;
return
//query splited to children
(j<=m ? _calc(i,j,l,m,v*2) : i>=m ? _calc(i,j,m,r,v*2+1)
: _calc(i,m,l,m,v*2) + _calc(m,j,m,r,v*2+1))
//and adding own addition
+ t[v].second * T(j-i);
}
};
Every time I see segment tree with pushes in this problem, my heart is bleeding... But! This is unnecessary, because this problem does not needs segment tree!
Reducing range_sum_range_add to range_sum_position_add
All following is described in 1-index numeration, and by range I mean half-interval $$$[L, R)$$$.
Let me remind you that sum on range can be reduced to sum on prefix (or suffix). And in the same way — adding on range can be reduced to adding on prefix (or suffix).
Two ways for each. Sum on range $$$[L, R)$$$ is equals to
(sum on prefix
R-1) — (sum on prefixL-1)(sum on suffix
L) — (sum on suffixR)
Similar, add $$$x$$$ on range $$$[L, R)$$$ is
add $$$x$$$ to prefix
R-1and subtract $$$x$$$ from prefixL-1add $$$x$$$ to suffix
Land subtract $$$x$$$ from suffixR
OK, suppose we have some changes of array (adding on prefix). We have for each $$$i$$$ value $$$a_i$$$ means this value is added on $$$i$$$-th prefix. How to calculate sum on particular prefix $$$k$$$? All added values inside prefix, i.e. $$$i \leq k$$$, must be added fully as $$$a_i \times i$$$. Values outside prefix, i.e. $$$k < i$$$, must be added as $$$a_i \times k$$$.
Lets keep two classic range_sum_position_add data structures. First, call it f, takes $$$a$$$ as is. Second, call it t, as $$$a_i \times i$$$. It means, if we need to proceed adding $$$x$$$ on prefix $$$i$$$, we call f.position_add(i, x) and t.position_add(i, x*i).
To answer prefix sum query we need:
all values inside: it will be
t.range_sum(1, i+1),all values outside: it will be
f.range_sum(i+1, n+1) * i.
That's all! With help of Binary Indexed Tree, as most popular rsq, we can achieve fast, non recursive and short way to implement required data structure.
We can change prefix/prefix to other three combinations and get similar formulas. As example, my code library have prefix/suffix version to achieve only prefix summation and suffix addition in both nested BITs:
template<class T>
struct rsq_add {
explicit rsq_add(size_t sz = 0): f(sz) {}
rsq_add(const vector<auto> &vals): f(size(vals)) {
for(size_t i=0; i<size(vals); ++i) {
T x = vals[i]; if(i) x-=T(vals[i-1]);
f[i].first+=x;
f[i].second+=x*T(i);
if(size_t j = i|(i+1); j<size(f)) {
f[j].first+=f[i].first;
f[j].second+=f[i].second;
}
}
}
void add(size_t l, size_t r, const T &val) {
if(l>=r) return ;
add_suf(l, val);
add_suf(r, -val);
}
T operator()(size_t l, size_t r) const {
if(l>=r) return T();
return sum_until(r) - sum_until(l);
}
inline T operator[](size_t i) const { return sum_until(i+1) - sum_until(i); }
private:
vector<pair<T,T>> f;
void add_suf(size_t pos, const T &val) {
T m = val * T(pos);
for(size_t i=pos; i<size(f); i|=i+1)
f[i].first+=val, f[i].second+=m;
}
T sum_until(size_t pos) const {
T a{}, b{};
for(size_t i=pos; i--; i&=i+1)
a+=f[i].first, b+=f[i].second;
return a*T(pos) - b;
}
};
Bonus: sqrt versions
It is well-known that with classic sqrt-decomposition queries can be proceeded in $$$O(\sqrt n)$$$ each. But with described reducing to range_sum_position_add we can achieve $$$O(1)$$$ / $$$O(\sqrt n)$$$ or $$$O(\sqrt n)$$$ / $$$O(1)$$$ versions for range_add / range_sum.
First is simple, adding to one element followed with adding to block contain this element, and summation is sum of $$$O(\sqrt n)$$$ blocks and sum of $$$O(\sqrt n)$$$ corner elements.
Second needs reducing range_sum_position_add to position_sum_range_add: lets support suffix sums (which gives sum on range as difference of two suffixes in $$$O(1)$$$) and changing one element $$$i$$$ affecting only suffixes sums from $$$0$$$ to $$$i$$$ (this part takes $$$O(\sqrt n)$$$).
Given a rooted tree.
Suppose query (v,d) is set of vertices in subtree of v in depth d from v.
Let's take all possible queries and leave only distinct sets.
Sum of sizes of these sets is $$$O(n\sqrt{n})$$$.
Actually, idk how to prove it. If you know proof, please post it here.
I met it in one Gerald's lecture with proof like "try to construct worst case and you see it".
I can construct such family of trees with $$$f(k)\approx \frac{n \sqrt n}{2}$$$ where $$$n(k) = \frac{k(k+1)}{2}$$$
Here tree with k=4: 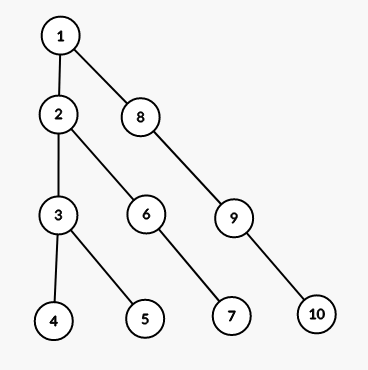
Only two times I tried to apply this as base of my solutions. But it was 1) useless — there are was easiest ones 2) painfull.
If you have some problems for this feature, post it please.
Problem
There is are famous problem for given array of numbers and number $$$K$$$ find minimums for all segments of length $$$K$$$.
More general variant: for given array of size $$$n$$$ and $$$q$$$ queries $$$[l_i,r_i]$$$ need to find minimums on segments at that $$$l_i \leq l_{i+1}$$$ and $$$r_i \leq r_{i+1}$$$. Solution must be $$$O(n+q)$$$.
To solve this problem we need sliding window method, where numbers from segments is window. Needed data structure should be able to push_back (add number to the end of window), pop_front (remove first element) and get_min — current minimum in window.
I was surprised to find that there are two types of such data structure. First is very popular and can be easily found in web. But type that I use whole life I can't find. I'll describe both of them.
Solution #1
The idea is to store sequence of increasing minimums. First minimum is minimum of whole window, second is minimum of elements after first minimum, and so on. For example, for window [2,3,1,5,4,8,7,6,9] sequence is [1,4,6,9].
When element is adding to the right of window (incR, push_back), the sequence changes as follows: all higher elements are gone from sequence, new element is goes to the end of sequence.
Couple of samples for [1,4,6,9]:
Adding 5: [1,4,6,9] -> [1,4] -> [1,4,5]
Adding 100: [1,4,6,9] -> [1,4,6,9,100]
Adding 0: [1,4,6,9] -> [] -> [0]
In removing left element from window (incL, pop_front) we need to know if first element of sequence is first element of window. Impossible to know this only by values, so we need to store sequence of pairs (value, index) except of only values. Previous example turns to [(1,2), (4,4), (6,7), (9,8)], where indices are numbered from zero. Bounds of window stored as pair of numbers $$$L$$$ and $$$R$$$. So, if first element of sequence is first element of window, that is its index equals to $$$L$$$, than only needed is to remove this first element from sequence.
Realization requires data structure that can efficiently perform operations of removing elements from left and right and adding new element to the right. Here we can use deque (std::deque in c++).
int inf = 2e9;
struct sliding_window{
deque<pair<int,int>> d;
int l, r;
sliding_window(){
l = r = 0;
}
void push_back(int x){
while(!d.empty() && d.back().first >= x) d.pop_back();
d.emplace_back(x,r);
++r;
}
void pop_front(){
if(d.front().second == l) d.pop_front();
++l;
}
int get_min(){
return d.empty() ? inf : d.front().first;
}
};
Solution #2
Represent window as two stacks: prefix of window stored in left stack $$$L$$$ so that first element of window in top of $$$L$$$, and suffix of window is stored in right stack $$$R$$$ so that last element of window in top of $$$R$$$.
[2,3,1,5,4,8,7,6,9]<-------|--------->
L = [5,1,3,2]R = [4,8,7,6,9]
When element is adding to the right of window (incR, push_back), it just goes to the top of $$$R$$$.
In removing left element from window (incL, pop_front), its pops from $$$L$$$, except of case when $$$L$$$ is empty. In this case we need to move right stack to left: while $$$R$$$ is not empty top of $$$R$$$ goes to the top of $$$L$$$. Example:
[4,3,1,2]|------->
L = []R = [4,3,1,2]
L = [2]R = [4,3,1]
L = [2,1]R = [4,3]
L = [2,1,3]R = [4]
L = [2,1,3,4]R = []
[4,3,1,2]<-------|
Now, after moving, we can pop top from $$$L$$$.
To get current minimum of window we need to know minimums of both stacks. Minimum of $$$R$$$ stored in $$$Rmin$$$ can be easily updated when elements are added to $$$R$$$.
In $$$L$$$ except of value need to store minimum of elements from this value to the bottom of stack. For example for stack [5,7,3,4,2,1,8,6] it is stack [5,5,3,3,2,1,1,1].
Thus, minimum in window is $$$Rmin$$$ or top of $$$L$$$.
int inf = 2e9;
struct sliding_window{
vector<int> l, r;
int rmin;
sliding_window(){
rmin = inf;
}
void push_back(int x){
r.push_back(x);
rmin = min(rmin, x);
}
void pop_front(){
if(l.empty()){
for(int mn = inf; !r.empty();){
mn = min(mn, r.back());
l.push_back(mn);
r.pop_back();
}
rmin = inf;
}
l.pop_back();
}
int get_min(){
int res = rmin;
if(!l.empty()) res = min(res, l.back());
return res;
}
};
Notes
Personally, I think second solution is simpler for understanding, but first more easy to code.
Both solutions can be upgraded to operation push_front, but seems like its useless.
We have n points (xi, yi). Let both x and y be different and from [1, n].
Initially, all points have zero value.
Two types of queries:
1) add X — adding +1 to all points with xi ≤ X
2) sum Y — calculate sum of values of points with yi ≤ Y
What is best known solution? (Problem not from running contest).
I've heard more about how vector<bool> is slow, and we need to dodge him or use vector<char>.
But today I ran some tests in "Codeforces custom test" with GNU G++.
First simple erato sieve
//N = 3e7
for(int i=2;i<N;++i) if(!u[i]) for(int j=i*2;j<N;j+=i) u[j] = 1;
int cnt = 0;
for(int i=0;i<N;++i) if(u[i]) ++cnt;
cout<<cnt<<endl;
Depends on u:
bool u[N] : 420 ms, 31204 KB
vector<bool> u(N): 218 ms, 5484 KB
vector<char> u(N): 451 ms, 31164 KB
You can say like "memory constant speed up this code"
Second.
//N = 1e4
double total = 0;
for(int it=0;it<N;++it){
for(int i=0;i<N;++i){
int x = rand()%N;
u[x] = 1;
}
for(int i=0;i<N;++i){
int x = rand()%N;
u[x] = 0;
}
for(int i=0;i<N;++i){
total+=u[i];
u[i] = 0;
}
}
cout<<total/N<<endl;
bool u[N] : 2683 ms, 1860 KB
vector<bool> u(N): 2667 ms, 1832 KB
vector<char> u(N): 2620 ms, 1868 KB
We see its equal!
So maybe its not so bad? Or you have examples where vector<bool> is really slower than alternatives?
Your given a simple task:
For given number 2 ≤ n ≤ 1018 check prime or not it is.
Limits are: 1 second TL, 16Mb ML.
And we have solution:
bool isprime(LL n){
if(n<2) return false;
for(LL i=2;i*i*i<=n;++i) if(n%i==0) return false;
for(int it=0;it<1e5;++it){
LL i = rand()%(n-1)+1;
if(__gcd(i,n)!=1) return false;
if(mpow(i,n-1,n)!=1) return false;
}
return true;
}
where rand() returns 64-bit random integer and mpow(a,b,m) is ab modulo m.
Can you challenge this solution?
Hi people! I interested in problems with template name "Count of subrectangles" or "Best subrectangle" in rectangle. For example some well-known problems:
In given matrix of zeros and ones find subrectangle that contains only zeros and has largest area. It can be solved in O(n2).
In given matrix of integers find subrectangle with largest sum. It can be solved in O(n3).
Can you give me links or just statements on similar problems?
Here problems that i remembered:
Please, gimme other problems, any links in contests or archives:) I will add it here later.
Production will stops iff exists integer K ≥ 0 such a·2K is divisible by m. From this fact follows that K maximum will be about O(log2(m)). So if we modeling some, for example, 20 days and production does not stop, then it will never stop and answer is "No". Otherwise answer is "Yes".
Let us find minimum length needed to cover points by Ox. It is Maximum(xi) - Minumum(xi). The same in Oy — Maximum(yi) - Minumum(yi). Since we need a square city to cover all the mines, then we need to set length of this square to the maximum from those two values.
Let us define function f(L, R), that gives answer to the query. It looks follows:
if L = R then f(L, R) = L;
else if 2b ≤ L, where b — maximum integer such 2b ≤ R, then f(L, R) = f(L - 2b, R - 2b) + 2b;
else if 2b + 1 - 1 ≤ R then f(L, R) = 2b + 1 - 1;
else f(L, R) = 2b - 1.
Total complexity is O(logR) per query.
Let us iterate over all different aj. Since we need to maximize 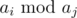 , then iterate all integer x (such x divisible by aj) in range from 2aj to M, where M — doubled maximum value of the sequence. For each such x we need to find maximum ai, such ai < x. Limits for numbers allow to do this in time O(1) with an array. After that, update answer by value
, then iterate all integer x (such x divisible by aj) in range from 2aj to M, where M — doubled maximum value of the sequence. For each such x we need to find maximum ai, such ai < x. Limits for numbers allow to do this in time O(1) with an array. After that, update answer by value 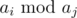 . Total time complexity is O(nlogn + MlogM).
. Total time complexity is O(nlogn + MlogM).
Note, that d-sorting is just a permutation (call it P), because it does not depends on characters in string. Look at shuffling operation in different way: instead of going to the next substring and sort it, we will shift string to one character left. It remains to understand that shift of string the permutation too (call it C). Now its clear, we need to calculate S·P·C·P·C... = S·(P·C)n - k + 1. And after that shift string for k - 1 character to the left for making answer to the shuffling operation. Here we use the multiplication of permutations. Since they are associative, that we can use binary algorithm to calculate (P·C)n - k + 1. Total time complexity is O(nmlogn).
Let us note, that in optimal answer any segment that making a group contains their minimum and maximum values on borders. Otherwise it will be better to split this segment to two other segments. Another note that is every segment in optimal solution is strictly monotonic (increasing or decreasing). Paying attention to the interesting points in sequence which making local maximums (i. e. ai - 1 < ai > ai + 1), local minimums (ai - 1 > ai < ai + 1), and point adjacent to them. Solve the problem by dynamic programming: Di is the answer in the prefix i. To calculate Di we need to look at no more than three previous interesting points and to previous Di - 1. Total time complexity is O(n).
Let us note that we can use binary search to find answer to the one query. Suppose at some moment was fixed height h and need to know will fit the rectangle with width w and height h to the segment of fence from l-th to r-th panel. Let us build data structure that can answer to this question. This will be persistent segment tree with unusual function inside: maximum number of consecutive ones in segment (maxOnes). In leaves of segment tree will be only numbers 0 and 1. To calculate this function need to know some other values, specifically:
len — length of the segment in vertex of segment tree, prefOnes — length of prefix that consists only of ones, sufOnes — length of the suffix consist only of ones.
These functions are computed as follows:
maxOnes is equal to max(maxOnes(Left), maxOnes(Right), sufOnes(Left) + prefOnes(Right));
prefOnes equals prefOnes(Right) + len(Left) in case of len(Left) = prefOnes(Left), and prefOnes(Left) otherwise;
sufOnes equals sufOnes(Left) + len(Right) in case of len(Right) = sufOnes(Right), and sufOnes(Right) otherwise;
len = len(left) + len(Right);
Left и Right — it is left and right sons of vertex in segment tree.
As mentioned above, tree must be persistent, and it must be built as follows. First, builded empty tree of zeros. Next in position of highest plank need to put 1. The same doing for planks in decreasing order. For example if fence described with sequence [2, 5, 5, 1, 3] then bottom of segment tree will changed as follows:
[0, 0, 0, 0, 0] -> [0, 1, 0, 0, 0] -> [0, 1, 1, 0, 0] -> [0, 1, 1, 0, 1] -> [1, 1, 1, 0, 1] -> [1, 1, 1, 1, 1].
And we need to remember for all hi their version of tree. Now to answer the question we need to make query in our segment tree (that corresponding to height h) on segment [l, r]. If maxOnes form this query less than w, then rectangle impossible to put (otherwise possible).
Building of tree will take O(nlogn) time and memory. Time complexity to the one query will take O(log2n) time.
Hello everybody!
Today will be Codeforces Round #276, which take place in both divisions. Start time is 19:30 in moscow time (follow this link to see time in others zones). For preparing contest i say thanks to Zlobober, for translating to Delinur, and to MikeMirzayanov for project Codeforces.
Good luck to all, hope you will enjoy problems :)
UPD Score distribution will be dynamic (see more information here). Problems will be sorted in increasing order of difficulty, however, do not forget to read all problems before the end of the contest.
UPD The contest is over! Thanks to everyone who solved the problems despite everything. Analysis will be published later.
UPD Editorial can be found here.
Hello, CodeForces community! I'm happy to tell you about upcoming 256-th round, which will be held for the participants from second division. Participants from first division can take part out of the competition.
I hope, for all this anniversary round. For me it is the first round in which I am the author, in this I will be glad to see everyone. Want to say thanks Gerald for help with preparing contest, Delinur for translating, and of course MikeMirzayanov for CodeForces project.
I am from Krasnoyarsk, and the hero of tasks will be our team talisman Bizon-the-Champion. Hope you like to spend time with him :) See you and good luck!
UPD. Few hours before the start. Score distribution will be dynamic (see more information here)
UPD. Round is over! You can find editorial here.
Solution:7139559
Because rewards of one type can be on one shelf, lets calculate number of cups — a and number of medals — b. Minimum number of shelves that will be required for all cups can be found by formula (a + 5 - 1) / 5. The same with shelves with medals: (b + 10 - 1) / 10. If sum of this two values more than n then answer is "NO" and "YES" otherwise.
Solution:7139584
Consider each case separately. If we use only suffix automaton then s transform to some of its subsequence. Checking that t is a subsequence of s can be performed in different ways. Easiest and fastest — well-known two pointers method. In case of using suffix array we can get every permutation of s. If it is not obvious for you, try to think. Thus, s and t must be anagrams. If we count number of each letter in each string, we can check this. If every letter appears in s the same times as in t then words are anagrams. In case of using both structures strategy is: remove some letters and shuffle the rest. It is possible if every letter appears in s not less times than in t. Otherwise it is impossible to make t from s. Total complexity O(|s| + |t| + 26).
Solution:7139610
To solve this problem we need to understand some little things. First, every horizontally stroke must be as widely as possible. Second, under every horizontally stroke should be only horizontally strokes. So, if bottom of fence painted by horizontally stroke then number of this strokes must at least min(a1, a2, ..., an). These strokes maybe divides fence into some unpainted disconnected parts. For all of these parts we need to sum they answers. Now its clearly that solution is recursive. It takes segment [l, r] and height of painted bottom h. But we must not forget about situation when all planks painted with vertically strokes. In this case answer must be limited by r - l + 1 (length of segment). With given constrains of n we can find minimum on segment by looking all the elements from segment. Complexity in this case will be O(n2). But if we use for example segment tree, we can achieve O(nlogn) complexity.
Solution:7139620
Solution is binary search by answer. We need to find largest x such that amount of numbers from table, least than x, is strictly less than k. To calculate this count we sum counts from rows. In i th row there will be 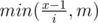 . Total complexity is O(nlog(nm)).
. Total complexity is O(nlog(nm)).
Solution:7139644
Learn how to transform Xi into Xi + 1. For this we need to concatenate lists of divisors for all elements of Xi. To do this efficiently, precalculate divisors of X (because for every i Xi consist of its divisors). It can be done by well-known method with 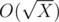 complexity. How to calculate divisors of divisors? Need to know that for the given constrains for X maximum number of divisors D(X) will be 6720 (in the number 963761198400), so divisors of divisors can be calculated in O(D2(X)) time. With this lists we can transform Xi into Xi + 1 in O(N) time, were N = 105 — is the limit of numbers in output. Now learn how to transform Xi into X2i. What says Xi? Besides what would be X after i steps, it can tell where goes everyone divisor of X after i - 1 steps. Actually, Xi is concatenation of all Yi - 1, where Y is divisor of X. For example, 103 = [1, 1, 1, 2, 1, 1, 5, 1, 1, 2, 1, 5, 1, 2, 5, 10] = [1] + [1, 1, 2] + [1, 1, 5] + [1, 1, 2, 1, 5, 1, 2, 5, 10] = 12 + 22 + 52 + 102. How to know which segment corresponds for some Y? Lets pos(Y) be the first index of Y in Xi. Then needed segment starts from pos(prev(Y)) + 1 and ends in pos(Y), where prev(Y) is previous divisor before Y in sorted list of divisors. So, to make X2i from Xi we need to know where goes every element from Xi after i steps. We know all its divisors — it is one step, and for every divisor we know where it goes after i - 1 step. Thus, we again need to concatenate some segments in correct order. It also can be done in O(N) time. How to find now Xk for every k? The method is similar as fast exponentiation:
complexity. How to calculate divisors of divisors? Need to know that for the given constrains for X maximum number of divisors D(X) will be 6720 (in the number 963761198400), so divisors of divisors can be calculated in O(D2(X)) time. With this lists we can transform Xi into Xi + 1 in O(N) time, were N = 105 — is the limit of numbers in output. Now learn how to transform Xi into X2i. What says Xi? Besides what would be X after i steps, it can tell where goes everyone divisor of X after i - 1 steps. Actually, Xi is concatenation of all Yi - 1, where Y is divisor of X. For example, 103 = [1, 1, 1, 2, 1, 1, 5, 1, 1, 2, 1, 5, 1, 2, 5, 10] = [1] + [1, 1, 2] + [1, 1, 5] + [1, 1, 2, 1, 5, 1, 2, 5, 10] = 12 + 22 + 52 + 102. How to know which segment corresponds for some Y? Lets pos(Y) be the first index of Y in Xi. Then needed segment starts from pos(prev(Y)) + 1 and ends in pos(Y), where prev(Y) is previous divisor before Y in sorted list of divisors. So, to make X2i from Xi we need to know where goes every element from Xi after i steps. We know all its divisors — it is one step, and for every divisor we know where it goes after i - 1 step. Thus, we again need to concatenate some segments in correct order. It also can be done in O(N) time. How to find now Xk for every k? The method is similar as fast exponentiation:
Xk = [X] when k = 0,
if k is odd then transform Xk - 1 to Xk,
if k is even then transform Xk / 2 to Xk.
This method takes O(logk) iterations. And one small trick: obviously that for X > 1 Xk starts from k ones, so k can be limited by N. Total complexity of solution is 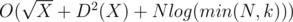 .
.
| Name |
|---|










