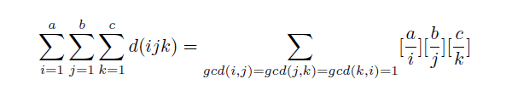Div2 A Colorful Stones (Simplified Edition) (Author: rng_58)
In this problem you just need to implement what is written in the statement. Make a variable that holds the position of Liss, and simulate the instructions one by one.
Div2 B Roadside Trees (Simplified Edition) (Author: snuke)
The optimal path of Liss is as follows: First she starts from the root of tree 1. Walk up the tree to the top and eat a nut. Walk down to the height min(h1, h2). Jump to the tree 2. Walk up the tree to the top and eat a nut. Walk down to the height min(h2, h3), ... and so on.
Div1 A / Div2 C Escape from Stones (Author: DEGwer)
In this problem, there are many simple algorithms which works in O(n). One of them (which I intended) is following:
You should prepare 2 vectors. If s[i] = 'l', you should push i to the first vector, and if s[i] = 'r', you should push i to the second vector. Finally, you should print the integers in the second vector by default order, after that, you should print the integers in the first vector in the reverse order.
This algorithm works because if Liss divides an interval into two intervals A and B and she enters A, she will never enter B.
Div1 B / Div2 D Good Sequences (Author: DEGwer)
The main idea is DP. Let's define dp[x] as the maximal value of the length of the good sequence whose last element is x, and define d[i] as the (maximal value of dp[x] where x is divisible by i).
You should calculate dp[x] in the increasing order of x. The value of dp[x] is (maximal value of d[i] where i is a divisor of x) + 1. After you calculate dp[x], for each divisor i of x, you should update d[i] too.
This algorithm works in O(nlogn) because the sum of the number of the divisor from 1 to n is O(nlogn).
Note that there is a corner case. When the set is {1}, you should output 1.
Div1 C / Div2 E Choosing Balls (Author: hogloid)
There are many O(Q * N * logN) solutions using segment trees or other data structures, but probably they will get time limit exceeded.
We can solve each query independently. First, let's consider the following DP algorithm.
dp[c] := the maximal value of a sequence whose last ball's color is c
For each ball i, we want to update the array. Let the i-th ball's color be col[i], the i-th ball's value be val[i], and the maximal value of dp array other than dp[col[i]] be otherMAX. We can update the value of dp[col[i]] to dp[col[i]] + val[i] × a or otherMAX + val[i] × b. Here, we only need to know dp[col[i]] and otherMAX. If we remember the biggest two values of dp array in that time and their indexes in the array, otherMAX can be calculated using the biggest two values, which always include maximal values of dp array other than any particular color.
Since the values of dp array don't decrease, we can update the biggest two values in O(1). Finally, the answer for the query is the maximal value of dp array.
The complexity of the described algorithm is O(QN).
Div1 D Colorful Stones (Author: rng_58)
First, let's consider a simpler version of the problem: You are given a start state and a goal state. Check whether the goal state is reachable from the start state.
Define A, B, C, and D as in the picture below, and let I be the string of your instructions. A and B are substrings of s, and C and D are substrings of t.
It is possible to reach the goal state from the start state if there exists an instruction I such that:
- 1 A is a subsequence of I.
- 2 B is not a subsequence of I.
- 3 C is a subsequence of I.
- 4 D is not a subsequence of I.
So we want to check if such string I exists. (string s1 is called a subsequence of s2 if it is possible to get s2 by removing some characters of s1)
There are some obvious "NO" cases. When D is a subsequence of A, it is impossible to satisfy both conditions 1 and 4. Similarly, B must not be a subsequence of C. Are these sufficient conditions? Let's try to prove this hypothesis.
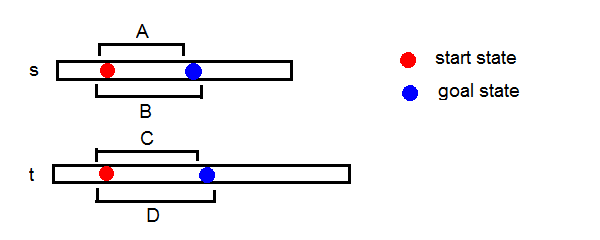
To simplify the description we will introduce some new variables. Let A', B', C', and D' be strings that can be obtained by removing the first characters of A, B, C, and D. Let c1 and c2 be the first characters of A and C.
Suppose that currently the conditions are satisfied (i.e. D is not a subsequence of A and B is not a subsequence of C).
- If c1 = c2, you should perform the instruction c1 = c2. The new quatruplet will be (A', B', C', D') and this also satisies the conditions.
- If c1 ≠ c2 and B' is not a subsequnce of C, you should perform the instruction c1. The new quatruplet will be (A', B', C, D) and this also satisies the conditions.
- If c1 ≠ c2 and D' is not a subsequnce of A, you should perform the instruction c2. The new quatruplet will be (A, B, C', D') and this also satisies the conditions.
What happens if all of the above three conditions don't hold? In this case A and C have the same length and A = c1c2c1c2..., B = c2c1c2c1. In particular the last two characters of A and B are swapped: there are different characters x and y and A = ...xy, B = ...yx. Now you found a new necessary condition! Generally, if A and B are of the form A = ...xy and B = ...yx, the goal state is unreachable. If the last instruction is x, Vasya must be in the goal before the last instruction, but then Vasya will go further after the last instruction. If the last instruction is y, we will also get a contradiction.
Finally we have a solution. The goal state is reachable from the start state if and only if D is not a subsequence of A, B is not a subsequnce of C, and A and C are not of the form A = ...xy, C = ...yx. The remaining part is relatively easy, so I'll leave it as an exercise for readers.
Div1 E Roadside Trees (Author: snuke)
For this problem there are slides: Please check here.
UPD: Thank you for pointing out mistakes. They are fixed.