I sometimes make problems and post them in Japanese local contest yukicoder. I want many people to know math problems I made, so I introduce some of them. Let's try!!
LCMST
Problem Statement
Consider a complete graph $$$G$$$ on $$$N$$$ vertices. The weight of edge between vertex $$$i$$$ and $$$j$$$ is least common multiple of $$$A_i$$$ and $$$A_j$$$. Find the total weight of the edges contained in a minimum spanning tree of $$$G$$$.
Constraints
- $$$2\leq N \leq 10^6$$$
- $$$1\leq A_i\leq 10^5$$$
- Time Limit is 4000ms
Sample
Consider the case where $$$N=3$$$ and $$$A=(2,3,4)$$$. The answer is $$$10$$$. This is optimal to draw edges between $$$(1,2),(1,3)$$$. These have weights $$$\mathrm{lcm}(A_1,A_2)=\mathrm{lcm}(2,3)=6, \mathrm{lcm}(A_1,A_3)=\mathrm{lcm}(2,4)=4$$$, respectively.
Hints
Simple Math ?
Problem Statement
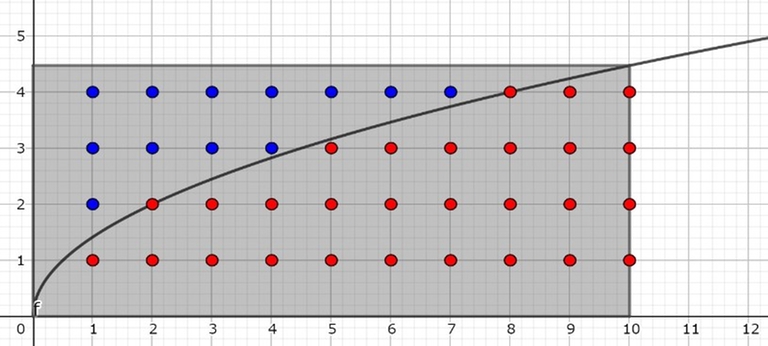
You are given integer $$$a,N$$$. Find $$$\displaystyle \sum_{i=1}^N \lfloor \sqrt{ai}\rfloor\ \mathrm{mod}\ 10^9+7$$$. You have $$$T$$$ test cases to solve.
Constraints
- $$$1\leq T \leq 10$$$
- $$$1\leq a \leq 10^6$$$
- $$$1\leq N\leq 10^{12}$$$
- Time Limit is 2000ms
Sample
Consider the case where $$$a=2$$$ and $$$N=5$$$. The answer is $$$\lfloor \sqrt{2} \rfloor+\lfloor \sqrt{4} \rfloor+\lfloor \sqrt{6} \rfloor+\lfloor \sqrt{8} \rfloor+\lfloor \sqrt{10} \rfloor=1+2+2+2+3=10$$$.
Hints
Simple Math !
Problem Statement
You are given integers $$$P,Q,K$$$. Find the $$$K$$$-th smallest positive integer $$$N$$$ that satisfies the following conditions:
- There exists a pair of nonnegative integers $$$(x,y)$$$ such that $$$N=Px+Qy$$$
You have $$$T$$$ test cases to solve.
Constraints
- $$$1\leq T \leq 10^4$$$
- $$$1\leq P,Q,K \leq 10^9$$$
- Time Limit is 2000ms
Sample
Consider the case where $$$P=3,Q=4,K=4$$$. The answer is $$$7$$$.
- When $$$N=1$$$, there is no pair $$$(x,y)$$$ of nonnegative integers satisfying $$$1=3x+4y$$$.
- When $$$N=2$$$, there is no pair $$$(x,y)$$$ of nonnegative integers satisfying $$$2=3x+4y$$$.
- When $$$N=3$$$, $$$(x,y)=(1,0)$$$ satisfies $$$3=3x+4y$$$.
- When $$$N=4$$$, $$$(x,y)=(0,1)$$$ satisfies $$$4=3x+4y$$$.
- When $$$N=5$$$, there is no pair $$$(x,y)$$$ of nonnegative integers satisfying $$$5=3x+4y$$$.
- When $$$N=6$$$, $$$(x,y)=(2,0)$$$ satisfies $$$6=3x+4y$$$.
- When $$$N=7$$$, $$$(x,y)=(1,1)$$$ satisfies $$$7=3x+4y$$$.