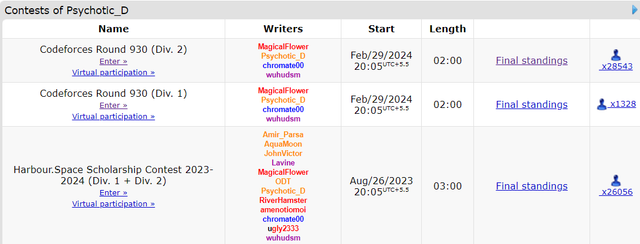
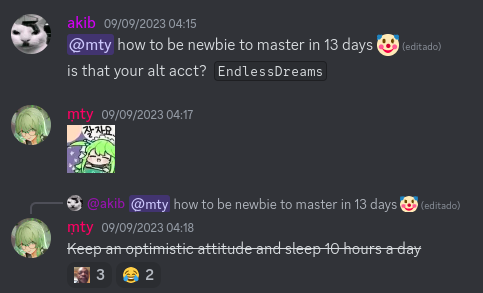
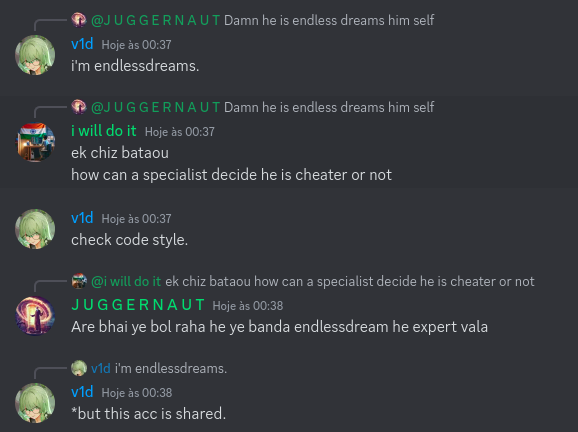
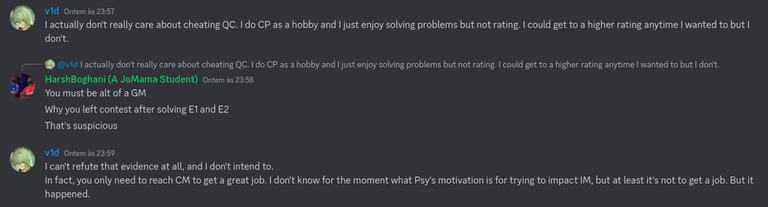
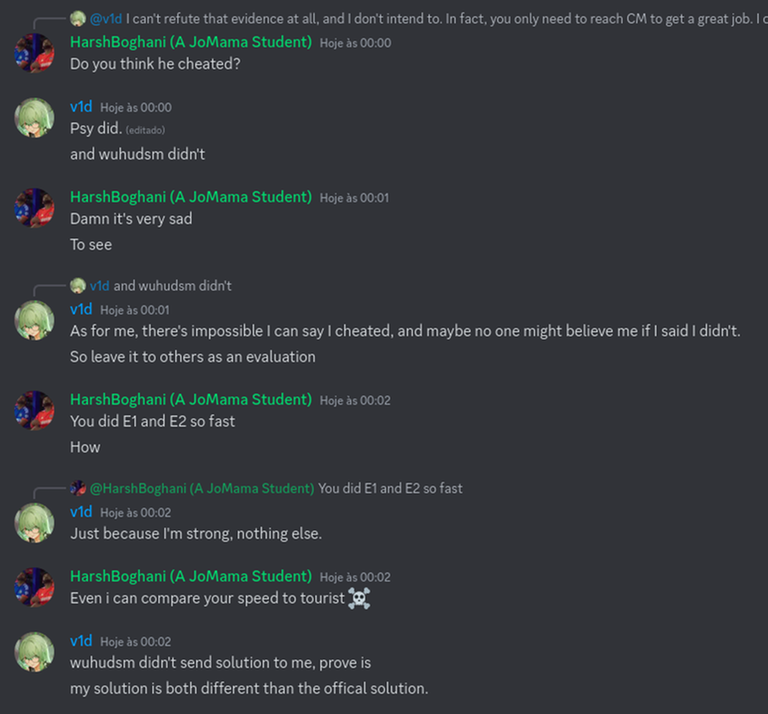
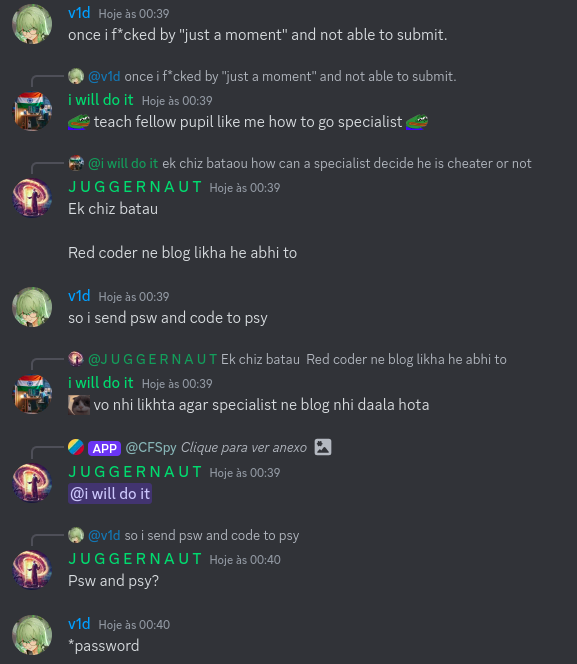
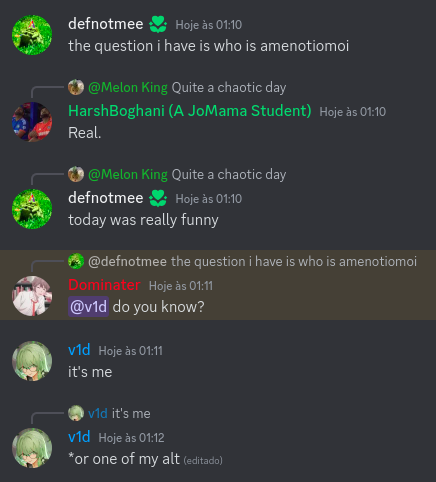
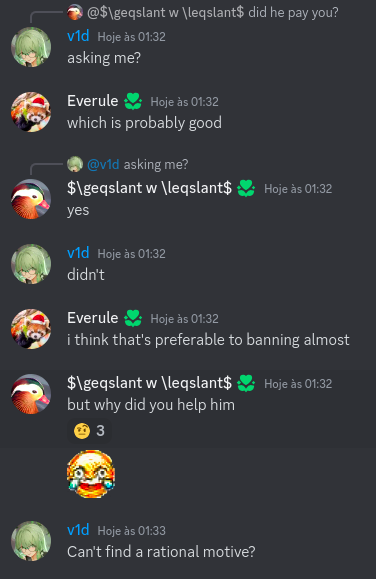
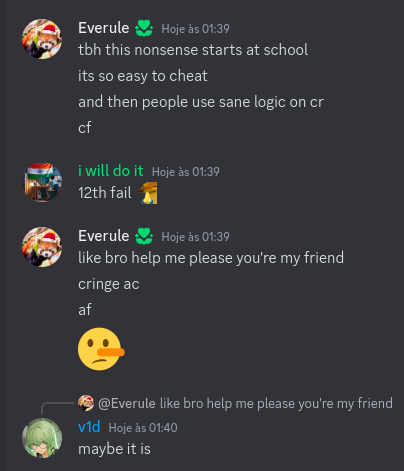
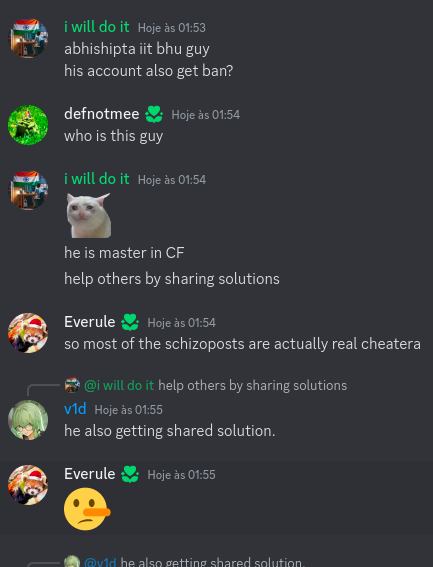
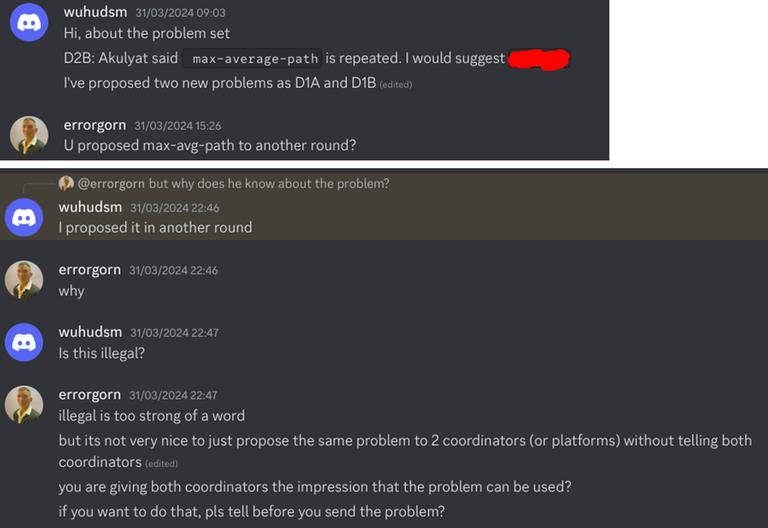
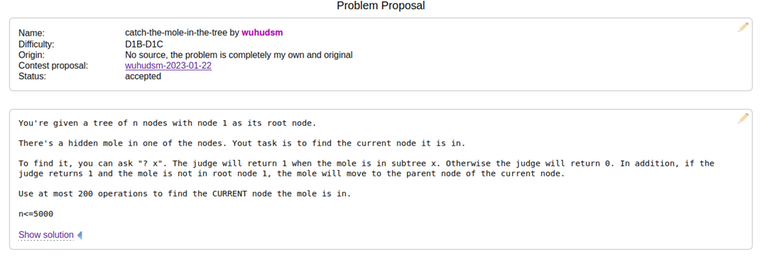
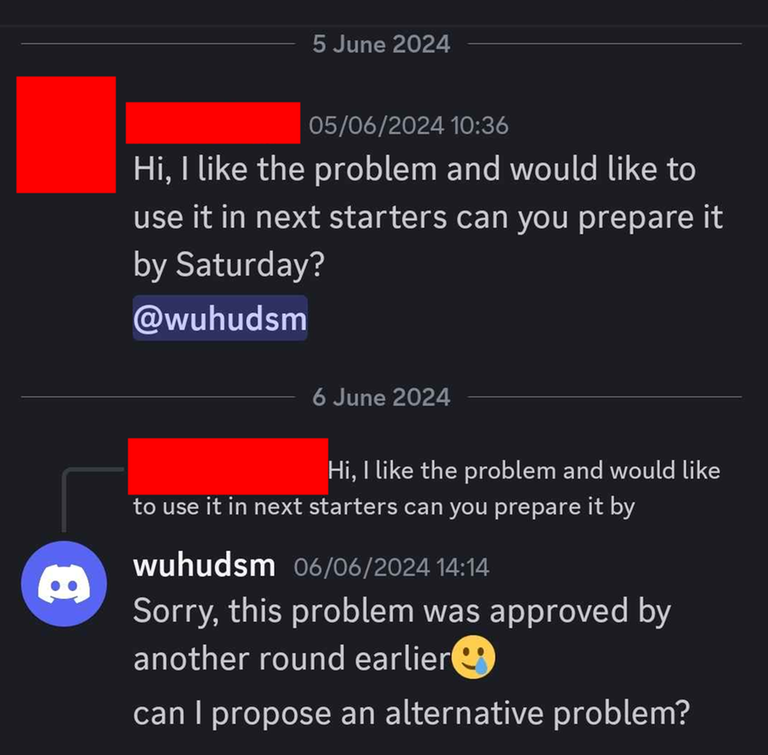
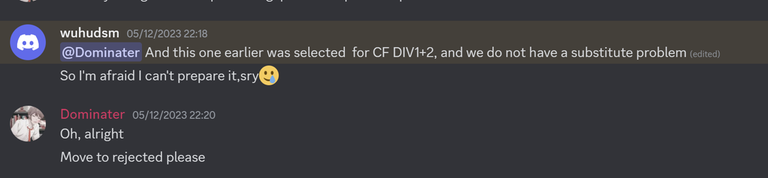
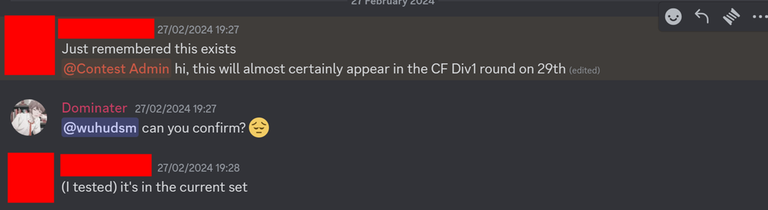
Today I want to talk about Psychotic_D AKA Dhruvil Kakadiya from Nirma University who claims to be a LEGIT IM but the reality is far from LEGIT. Today another blog was written by a person exposing him for the person he is but him and his so called friends made that blog vanish. Thats the platform of Codeforces for you where exposing cheater is secondary and cheating and maintaining their rating in anyway possible is primary. So, here we are with another blog with more proof that Dominater069 requested. Below are some of the past contests submission done by Psychotic_D which he claims is done because to check if he can solve harder problem and maintain the rating or not but in reality he waits for his friends group which includes some of the testers, GM, IM. As you have heard his friend wuhudsm has been exposed for using many rejected and proposed problems for the contest which i must tell u Dhruvil had the access to. He along with his group which includes wuhudsm amenotiomoi EndlessDreams Synergism and many more cheats and helps him in his contest. He posted a screenshot in the earlier blog which clearly stated that wuhudsm had sent something which had to do with the ongoing contest which he immediately told him to delete, after accessing it offcourse . Now he didnt say anything about the accusations rather he played the victim card and let Dominater069 fight his battles. Good thing giving your sword to an IGM, now your image is restored ig.
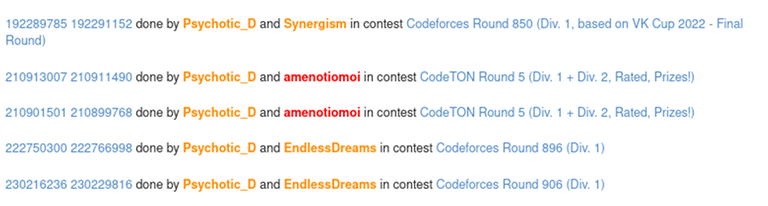
here are some screenshots with weird submission timings. 




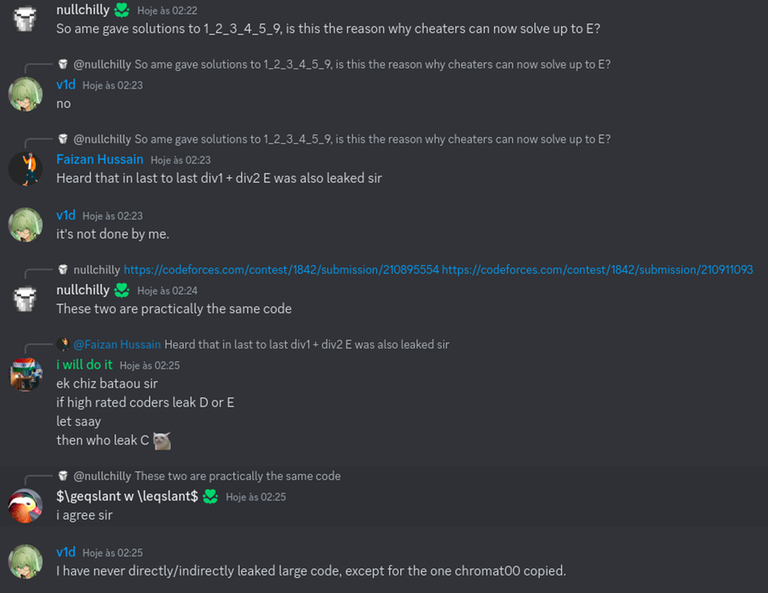
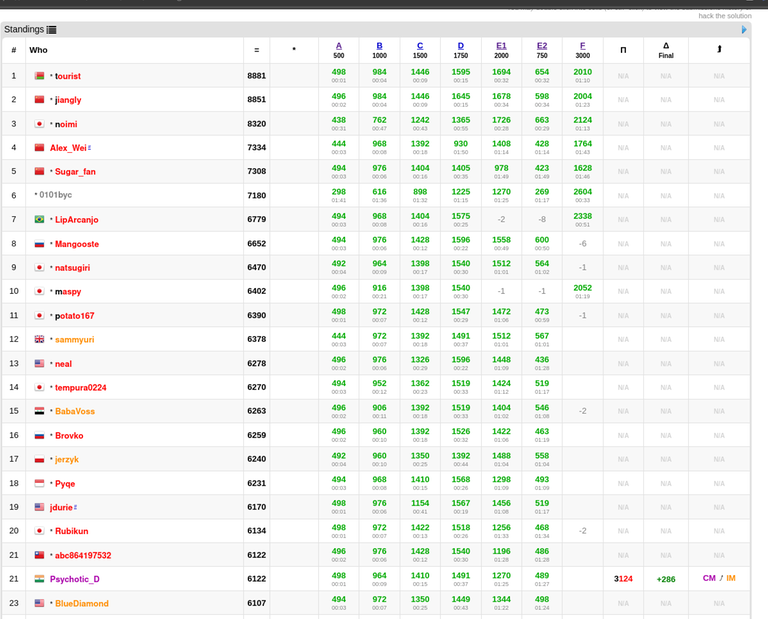
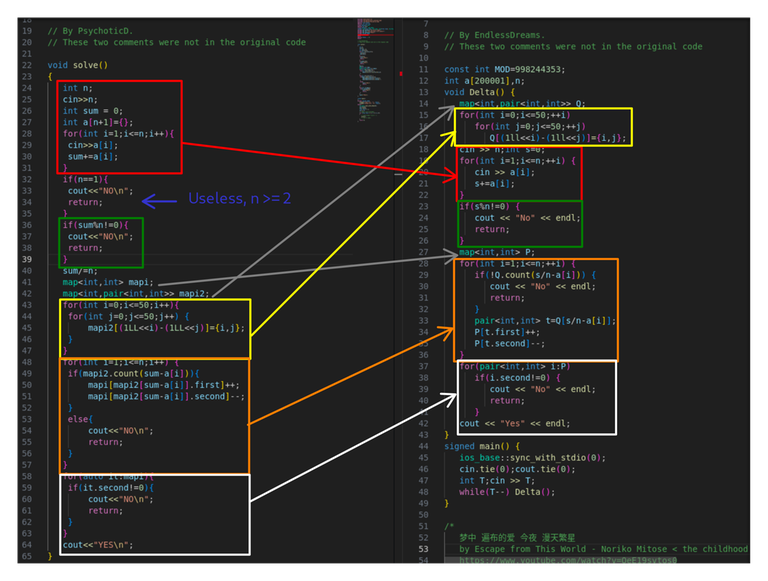
Now lets talk about the contest submission overlap which would have been flagged but I dont know what Codeforces was doing so it didnt.
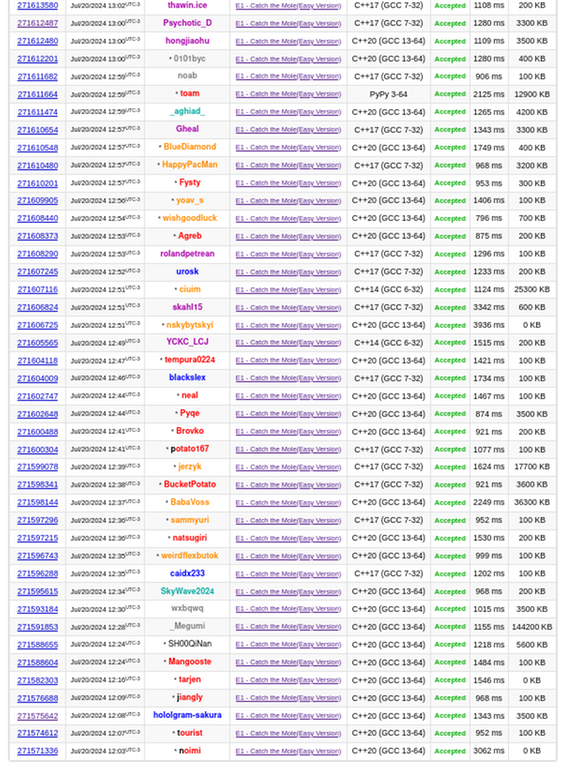
192289785 192291152 done by Psychotic_D and Synergism in contest Codeforces Round 850 (Div. 1, based on VK Cup 2022 - Final Round)
210913007 210911490 done by Psychotic_D and amenotiomoi in contest CodeTON Round 5 (Div. 1 + Div. 2, Rated, Prizes!)
210901501 210899768 done by Psychotic_D and amenotiomoi in contest CodeTON Round 5 (Div. 1 + Div. 2, Rated, Prizes!)
222750300 222766998 done by Psychotic_D and EndlessDreams in contest Codeforces Round 896 (Div. 1)
230216236 230229816 done by Psychotic_D and EndlessDreams in contest Codeforces Round 906 (Div. 1)
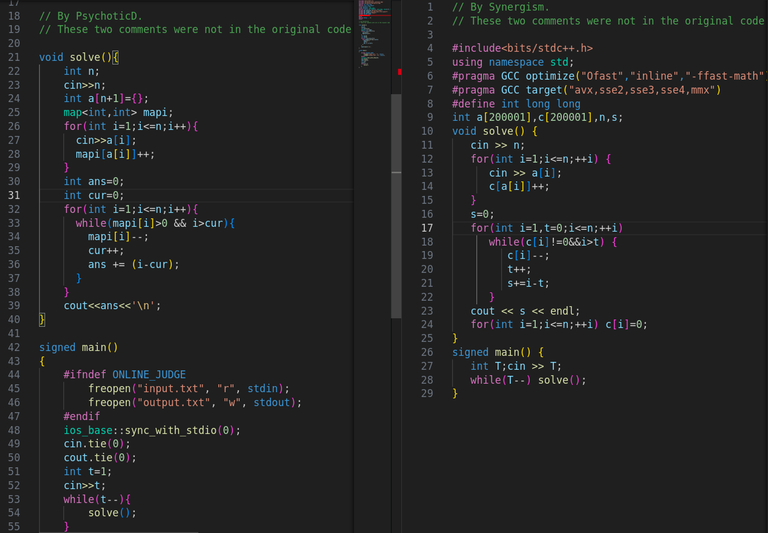
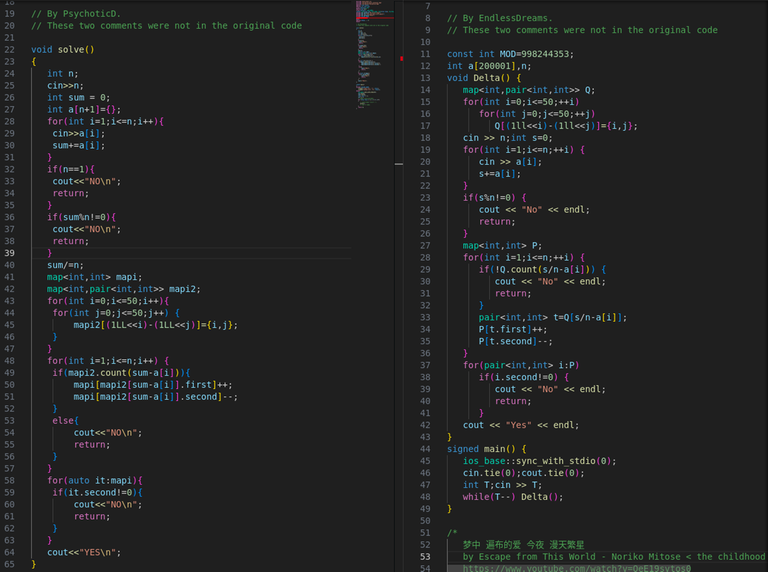
Now tell me one thing am I delusional or all the submisions are direct overlap with each other with clever changes to remove plagarism.
He is currently running IICPC, which is led by Vivek Gupta acraider, who posts on LinkedIn about cheating regularly.I dont know if he knew about his situation or not but now that he knows he should really take action about it. He is also teaching in TLE Eliminators which in fact is run by Priyansh Agarwal Priyansh31dec .
I have nothing against with that guy and i don't know him personally but i was noticing this for a long time and this cheating and scamming people just with his IM tag should stop.what he doing is very wrong and he should be punished for it.
There is a reason why us indians are shamed for being cheaters and he is one of the reason for it. People like Dominater069 are inspiration to people but it was very wrong of him protecting him without asking a simple question "DID YOU CHEAT OR ARE YOU LEGIT?" , this could have answered all his queries but he didnt and kept on defending him. Now i think he will not ask for more of the proofs as i have shown plenty .
If you really want more then I will give you more but it should be stopped before cheaters gloryify their fake rating and make thier name for themselves.
CC Priyansh31dec Vladosiya MikeMirzayanov acraider
I would have tagged the author wuhudsm too but he himself is in his cheating group so whats the point XD. Below attached is the proof for the accusation.
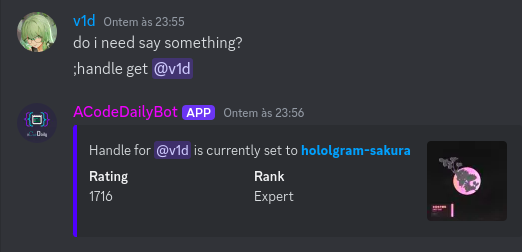
ps- This is not my id and is my classmate's and he agreed to give it to me to write a blog so dont bother telling me you too have a plag and you should be banned too and you are correct he should be too , The day Psychotic_D is banned is the day I myself will tell my friend to delete this id.
I hope codeforces will take action about this else everyone should help their friends cheat, because thats the message it will send.
Please correct me where I am wrong and help me in making him pay for his actions.
Thank you for listening.
Join the server and expose the cheaters.