td,dr: A 900, B1 1000, B2 1100, B3 1300, C1 1200, C2 1400, D1 1600, D2 1700, D3 2200, E1 1800, E2 2100.
You needed around 2000 rating to have a 50% prob of advancing to Round 2.
Hi everyone. GCJ round 1A took place yesterday. If you didn't participate, you may be wondering how hard it was, and what are your chances to pass round 1B or 1C and advance to round 2.
I provide below my estimate of the difficulty of the problems. The data and methods are the same I described in my previous post.
I am sure there is room for improvement, so again I welcome any feedback.
Method 1: The 50% Bucket
Approach and Data
Please see my previous post for more details. In short, I divide the contestants in buckets of rating, wide 100 points, and I see which bucket had a 50% probability of solving the problem.
Out of around 10'000 participants of GCJ 1A, 3'915 had a CF namesake. I removed a couple of outliers, like a 3400 rating participant who solved only A1 (maybe the CF coder and the GCJ participants are not the same person?), and the results are below.
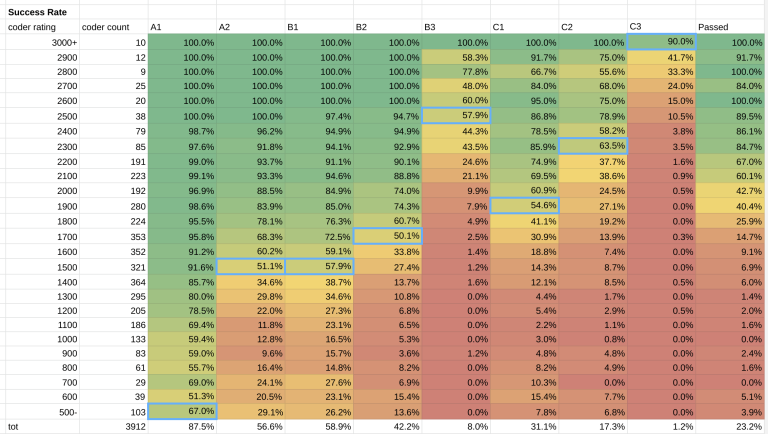
Results
This is the estimate: A1 500, A2 1500, B1 1500, B2 1700, B3 2500, C1 1900, C2 2300, C3 3000.
I think this approach is now working better than it did for the qualification round. This may be because everyone is trying to solve every problem, compared to the qualification round where there was little incentive to solve everything.
One problem that persists, is that among lowly rated participants there are coders performing very well, maybe too well, for their rating. These may be new accounts of seasoned coders. This lowers the estimated difficulty for example of A1. Was it really a 500 difficulty problem? Maybe it was something more.
Method 2: Inverse Prob Function
Approach and Data
Again, please see my previous post for more details.
In this round, the average contestant rating was 1594. I considered the rating buckets around the average, from 1500 to 1700. This includes about 1000 contestants.
CF rating system assumes that your chances of solving a problem is a function of your rating and of the problem difficulty, see here. We know the participants I kept have rating around 1600, we estimate their probability of solving a problem with the percentage of partecipants who solved it, and we can get the difficulty of the problem. The formula is $$$D=400 \cdot \log_{10} \left( \frac{1-p}{p} \right) + R$$$.
Results
This is the estimate: A1 1154, A2 1529, B1 1505, B2 1689, B3 2299, C1 1825, C2 1981, C3 2902.
The results are fairly in line with the previous method, which is a good sign.
A1 has higher rating now, around 1100. My impression is that the approach of inverting the prob function doesn't work very well for difficulties far away from contestants rating, so I do some average between estimates.
C2 difficulty instead dropped from 2300 to about 2000. Which one is more accurate? My personal impression is that 2300 is a bit too much, but I welcome your input here.
My Estimate
I put together the two estimates above, and I get this: A1 500, A2 1500, B1 1500, B2 1700, B3 2500, C1 1900, C2 2300, C3 3000.
What do you think?






