Here is a solution for the problem 534B - Пройденный путь
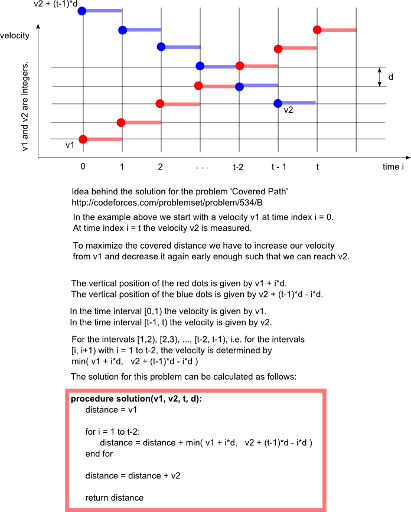
Here is my submission in Python: 10688757.
At least that's how I understood the problem by reading other people's solutions here. The only problem with that interpretation though is that there is a sudden jump in the velocity at times 1, 2, ..., t-1, so the velocities look like step functions. This would mean that the acceleration at those times is infinite. Did I misinterpret the problem?









 , but keep in mind that the worst-case runtime is
, but keep in mind that the worst-case runtime is 
