Hi everyone, I became grandmaster today so I decided to go down memory lane and review every problem I have ever done in a CodeForces contest to look back and see every technique and algorithm I had to use to become a grandmaster. I am not sure how useful this is, I mostly think it's fun to look at all the old solutions I wrote and how different it was from how I write code now. The main takeaway is that, as many people have said before, you don't need to know or memorize a bunch of advanced algorithms to become grandmaster. As you will see, there are many problems where I just used "ad hoc reasoning," meaning there's not a standard technique I used to solve the problem and you just need to make some clever mathematical observations to solve the problem. Also, there are many popular algorithms that I have never needed in a CodeForces contest despite being a grandmaster:
- Sparse tables, Fenwick trees, and segment trees
- String algos, like rolling hashes, Knuth-Morris-Pratt, suffix arrays, and Aho-Corasick
- Shortest path algos, like Dijkstra's algorithm, Bellman-Ford, and Floyd-Warshall
- Flow algos, like Edmonds-Karp, Dinic's, and push-relabel
- Convex hull trick
- Fast Fourier transform and number theoretic transform
This isn't to say that learning algorithms is bad—I love reading cp-algorithms.com and learning new algorithms—and I have used many of these algorithms in other contests, like CodeChef, ICPC, and Google Code Jam, but practicing consistently and getting better at ad hoc reasoning and your general problem-solving abilities matter much more.
CodeForces Round #362 (Div. 2): Rating went from 1500 to 1504 (back then, default rating was 1500 instead of 0)
Codeforces Round #363 (Div. 2): Rating went from 1504 to 1536 (+36)
- Problem A: Brute force
- Problem B: Brute force
- Problem C: Ad hoc reasoning and basic bitmasks (there is a dynamic programming solution, but that's not how I solved it)
Codeforces Round #553 (Div. 2): Rating went from 1540 to 1566 (+26)
- Problem A: Brute force
- Problem B: Brute force and bitwise operations
- Problem C: Ad hoc reasoning and math
Codeforces Round #570 (Div. 3): Rating went from 1566 to 1732 (+166)
- Problem A: Basic number theory
- Problem B: Ad hoc reasoning and math
- Problem C: Ad hoc reasoning and math
- Problem D: Greedy and priority queue
- Problem E: Ad hoc reasoning with strings (there is a BFS solution, but that's not how I solved it)
- Problem H: Dynamic programming (I used the count unique subsequences of a given length algorithm)
Educational CodeForces Round 68: Rating went from 1732 to 1766 (+44)
- Problem A: Ad hoc reasoning and math
- Problem B: Brute force and row/column sums
- Problem C: Ad hoc reasoning with strings and subsequences
- Problem D: Game theory
CodeForces Global Round 4: Rating went from 1776 to 1807 (+31)
- Problem A: Greedy
- Problem B: Dynamic programming
- Problem C: Binary exponentiation
- Problem D: Ad hoc reasoning with graphs
- Problem E: Deques
Educational Codeforces Round 74: Rating went from 1807 to 1920 (+113)
- Problem A: Ad hoc reasoning and math
- Problem B: Greedy and sorting
- Problem C: Greedy
- Problem D: Ad hoc reasoning and combinatorics
Codeforces Round #600 (Div. 2): Rating went from 1920 to 1877 (-43)
- Problem A: Ad hoc reasoning and math
- Problem C: Sorting, prefix sums, and dynamic programming
- Problem D: Depth-first search and connected components
Codeforces Round #601 (Div. 2): Rating went from 1877 to 2005 (+128)
- Problem A: Ad hoc reasoning and math
- Problem B: Ad hoc reasoning with graphs and sorting
- Problem C: Ad hoc reasoning with graphs and permutations
- Problem D: Ad hoc reasoning with grids
- Problem E1: Greedy
Codeforces Global Round 14: Rating went from 2005 to 1877 (-128)
- Problem A: Ad hoc reasoning with sorting
- Problem B: Ad hoc reasoning with number theory
- Problem C: Greedy and priority queue
Deltix Round, Spring 2021: Rating went from 1877 to 1975 (+98)
CodeForces LATOKEN Round 1: Rating went from 1975 to 1974 (-1)
- Problem A: Ad hoc reasoning with grids
- Problem B: Ad hoc reasoning and math
- Problem C: Cycle decomposition and binary exponentiation
- Problem D: Ad hoc reasoning with trees
Codeforces Round #729 (Div. 2): Rating went from 1974 to 2132 (+158)
- Problem A: Ad hoc reasoning and math
- Problem B: Ad hoc reasoning with number theory
- Problem C: Ad hoc reasoning with number theory
- Problem D: Binary exponentiation and dynamic programming
- Problem E1: Dynamic programming and combinatorics (I used the count permutations with given number of inversions algorithm, the numbers of permutations with a given number of inversions are also known as Mahonian numbers)
Hello 2022: Rating went from 2132 to 2085 (-47)
Codeforces Round #765 (Div. 2): Rating went from 2085 to 2092 (+7)
- Problem A: Greedy and bitwise operations
- Problem B: Ad hoc reasoning and maps
- Problem C: Dynamic programming
Educational Codeforces Round 122: Rating went from 2092 to 2168 (+76)
- Problem A: Ad hoc reasoning with number theory
- Problem B: Greedy
- Problem C: Brute force
- Problem D: Dynamic programming
- Problem E: Kruskal's algorithm and binary search tree maps
Codeforces Round #808 (Div. 1): Rating went from 2168 to 2138 (-30)
Codeforces Global Round 23: Rating went from 2138 to 2239 (+101)
- Problem A: Ad hoc reasoning and math
- Problem B: Greedy with stacks
- Problem C: Ad hoc reasoning with permutations
- Problem D: Tree DP
- Problem E: Ad hoc reasoning, with inspiration from binary search
Codeforces Global Round 24: Rating went from 2239 to 2291 (+52)
- Problem A: Ad hoc reasoning and math
- Problem B: Ad hoc reasoning with number theory
- Problem C: Prefix sums and maps
- Problem D: Modular arithmetic, extended Euclidean algorithm, and combinatorics
- Problem E: Greedy, sorting, and binary search tree sets
Good Bye 2022: 2023 is NEAR: Rating went from 2291 to 2358 (+67)
- Problem A: Greedy and binary search tree sets
- Problem B: Ad hoc reasoning with permutations
- Problem C: Ad hoc reasoning with number theory (I did use Miller-Rabin, but only to generate the primes <100, which could have been hardcoded instead)
- Problem D: Disjoint set union, and I also used DFS trees for the intuition behind this solution
- Problem E: Tree DP and extended Euclidean algorithm
Hello 2023: Rating went from 2358 to 2331 (-27)
- Problem A: Ad hoc reasoning with simulations
- Problem B: Ad hoc reasoning and math
- Problem D: IntervalContainer and maps
- Problem E: Sorting and ad hoc reasoning with graphs and strongly connected components
TypeDB Forces 2023: Rating went from 2331 to 2416 (+85)
- Problem A: Ad hoc reasoning and math
- Problem B: Miller-Rabin, Pollard's rho algorithm, and number theory
- Problem C: Dynamic programming
- Problem D: Tarjan's SCC algorithm and DP over directed acylic graphs
- Problem E: Greedy and bitwise operations
- Problem F: Binary exponentiation, extended Euclidean algorithm, and cycle decomposition









 edges per query.
edges per query.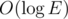 to process. There are
to process. There are 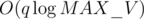 edges, meaning each edge is
edges, meaning each edge is 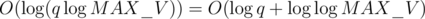 to process.
to process.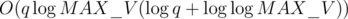 overall. However,
overall. However, 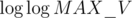 term and simply has
term and simply has 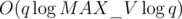 . How did they get rid of the
. How did they get rid of the 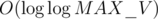 term in the analysis? Did I do something wrong here?
term in the analysis? Did I do something wrong here?
