Codeforces now has 342281 testcases. But how many of these are actually relevant?
Let's call a test redundant if nobody has ever submitted a solution that failed on that test. Here's a graph showing what percentage of testcases are redundant over all rounds.

Turns out to be that 173195 tests out of the 342281 tests are actually redundant — no verdict would change if these tests were never there. That's around 50%. I actually expected more, but still, a lot of testcases are redundant.
Here is another representation of data, where the y-axis shows how many problems of each percentage of redundancy.
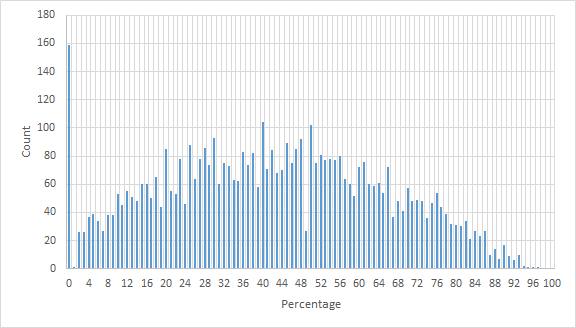
Codeforces can take advantage of this and save resources by not running these tests at all. But how long should we wait before deciding that the current non-redundant testcases are enough?
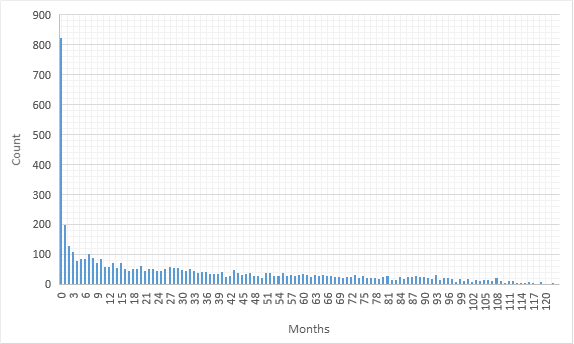
As you can see a lot of problems get saturated in the first month. But many others don't; however, don't treat these non-redundant testcases as absolutely essential because a solution failing at one of them doesn't mean that it passes all others (for example, all problems have solutions failing at the first testcase).
How many testcases, do you think, does a problem need on average if we were to pick them the most optimal way?
Thanks zoooma13 for sharing ideas and helping collecting the data.










