514A - Chewbaсca and Number
Author: Rebryk
It is obvious that all the digits, which are greater than 4, need to be inverted. The only exception is 9, if it's the first digit.
Complexity: 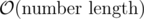
514B - Han Solo and Lazer Gun
Author: Antoniuk
Let's run through every point, where the stormtroopers are situated. If in current point stormtroopers are still alive, let's make a shot and destroy every stormtrooper on the same line with gun and current point.
Points (x1, y1), (x2, y2), (x3, y3) are on the same line, if (x2 - x1)(y3 - y1) = (x3 - x1)(y2 - y1).
Complexity: 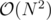
514C - Watto and Mechanism
Author: Rebryk
While adding a string to the set, let's count its polynomial hash and add it to an array. Then let's sort this array. Now, to know the query answer, let's try to change every symbol in the string and check with binary search if its hash can be found in the array (recounting hashes with 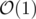 complexity). If the hash is found in the array, the answer is "YES", otherwise "NO".
complexity). If the hash is found in the array, the answer is "YES", otherwise "NO".
Complexity: 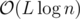 , where L is total length of all strings.
, where L is total length of all strings.
514D - R2D2 and Droid Army
Author: Rebryk
To destroy all the droids on a segment of l to r, we need to make 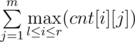 shots, where cnt[i][j] — number of j-type details in i-th droid. Let's support two pointers — on the beginning and on the end of the segment, which we want to destroy all the droids on. If we can destroy droids on current segment, let's increase right border of the segment, otherwise increase left border, updating the answer after every segment change. Let's use a queue in order to find the segment maximum effectively.
shots, where cnt[i][j] — number of j-type details in i-th droid. Let's support two pointers — on the beginning and on the end of the segment, which we want to destroy all the droids on. If we can destroy droids on current segment, let's increase right border of the segment, otherwise increase left border, updating the answer after every segment change. Let's use a queue in order to find the segment maximum effectively.
Complexity: 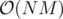
514E - Darth Vader and Tree
Author: Antoniuk
It's easy to realize that  , where dp[i] is number of vertices, which are situated on a distance i from the root, and cnt[j] is number of children, which are situated on a distance j. Answer
, where dp[i] is number of vertices, which are situated on a distance i from the root, and cnt[j] is number of children, which are situated on a distance j. Answer 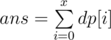 .
.
Let the dynamics condition

Let's build a transformation matrix of 101 × 101 size

Now, to move to the next condition, we need to multiply A by B. So, if matrix C = A·Bx - 100, then the answer will be situated in the very right cell of this matrix. For x < 100 we'll find the answer using dynamics explained in the beginning.
In order to find Bk let's use binary power.
Complexity: