Years ago, when I was in college and decently good at competitive programming, I applied for a Google internship and was confident of decimating the interviews — given how well I knew the basic as well as advanced algorithms and data structures — and my cracking coding speed which produced bug free code (mostly). I remember the interviewer asking me a question about substring matching, which turned out to be a piece of cake with a custom string hashing function and a hashmap. I was done within half an hour and went to sleep imagining if Google internship would be as fun as they say — team outings, free food, schwag etc.
A few days later, I got a rejection email. And then I went and talked to my college seniors about what had really happened. I had totally misunderstood the objective of the interview. I had displayed skills that are relevant to ACM ICPC and CF online judges, but not to human beings. I had displayed only a subset of skills that are required to be a good software engineer (debatable, but at least that's how the interview process goes).
I've interviewed hundreds of candidates at my time at Google — many of them rated highly on various coding platforms — but lacking the basic style of a conversation that could convince me to work with them. It's disappointing to see the lack of some basic guidance, given how much these folks can achieve.
For the same reasons, I've started with an initiative which this community may find useful. It's a #WeeklyCodingInterview series, where I post a typical, but unique, interview question, along with follow ups, that folks can try for a week. At the end of the week, on my Youtube channel I provide the fundamental approaches to not only the problem, but also the whole topic, along with interviewer insights such as — how to approach, what are the common mistakes, how to communicate, what is the hiring bar at Google, etc.
Hope the community would find it useful.















 .
. 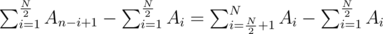 . If the array is of odd length, we can simply skip the middle element. This can be maximized by putting the large numbers in the right half, and the small numbers in the left half. One good way to do this is to simply sort the array in ascending order.
. If the array is of odd length, we can simply skip the middle element. This can be maximized by putting the large numbers in the right half, and the small numbers in the left half. One good way to do this is to simply sort the array in ascending order.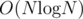 .
.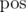 , the contribution of this position in answer is
, the contribution of this position in answer is . Following code explains the transition between states.
. Following code explains the transition between states. 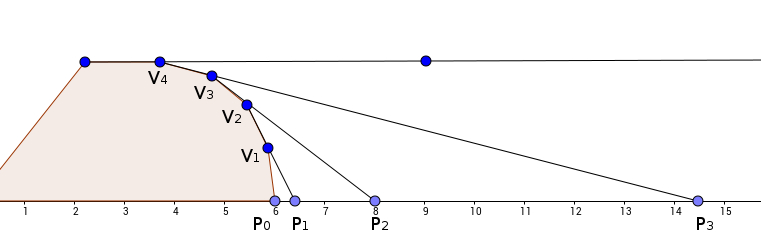
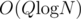 .
.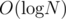
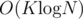
 and those with
and those with  . Apply
. Apply 
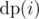 denoting answer for
denoting answer for 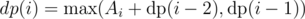 (two cases: choose
(two cases: choose  as the answer for subtree of node
as the answer for subtree of node 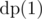 .
.  .
. 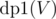 and
and 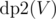 , denoting maximum coins possible by choosing nodes from subtree of node
, denoting maximum coins possible by choosing nodes from subtree of node 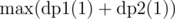 .
.  (since we cannot include any of the children) and
(since we cannot include any of the children) and 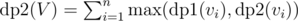 (since we can include children now, but we can also choose not include them in subset, hence max of both cases).
(since we can include children now, but we can also choose not include them in subset, hence max of both cases). 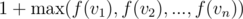 , because we are looking at maximum path length possible from children of
, because we are looking at maximum path length possible from children of  .
. 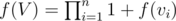 . Now, is our solution complete?
. Now, is our solution complete? 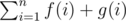 i.e. for each child we add to
i.e. for each child we add to 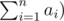 since we are forming a sub tree of size
since we are forming a sub tree of size 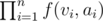 for all possible distinct sequences
for all possible distinct sequences 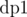 . We say
. We say 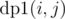 as number of ways to choose a total of
as number of ways to choose a total of 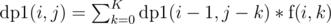 , i.e. we are iterating over
, i.e. we are iterating over 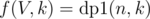 .
.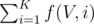 for all nodes
for all nodes 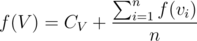 , since with same probability we'll move down each of the children.
, since with same probability we'll move down each of the children. 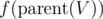 if tree is rooted at
if tree is rooted at 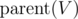 , if we don't consider contribution of subtree of
, if we don't consider contribution of subtree of 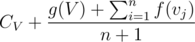 . To realise this is correct, have a look at definition of
. To realise this is correct, have a look at definition of 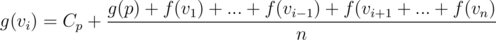 , since
, since 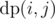 as minimum additions required to make subtree of node
as minimum additions required to make subtree of node 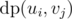 . Now, to all nodes in
. Now, to all nodes in  and by solving this assignment problem, we can get value of
and by solving this assignment problem, we can get value of 
