Throughout the year, Google Code Jam hosts online Kickstart rounds to give participants the opportunity to develop their coding skills, get acquainted with Code Jam’s competition arena, and get a glimpse into the programming skills needed for a technical career at Google.
Each Kickstart round gives participants 3 hours to solve challenging, algorithmic problems developed by Google engineers. Participating is a fun way to grow your coding skills—and potentially explore opportunities at Google.
Inviting you to solve some fun and interesting problems on Sunday, May 27, 2018 05:00 UTC.
Dashboard can be accessed here during the contest. Problem analysis will be published soon after the contest.











I think the date should be May 27, 2018!
How to solve C-large?
Count the contribution of each A[i] in the final answer.
Consider the contribution of each A[i] in Powerm. It is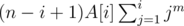 .
.
Then total contribution of A[i] is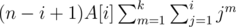 .
.
Call the double summation as B[i]. Then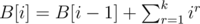 . The second term is sum of a geometric progression. Hence, complexity is O(n).
. The second term is sum of a geometric progression. Hence, complexity is O(n).
Is there a solution better than brute force for B ?
When contest analysis will be online ?
https://codejam.withgoogle.com/codejam/contest/3254486/dashboard#s=a
Sorry but this link is from Round G, 2017 :(
Sorry, I don't know what I was thinking when I posted that link.
What is the solution of B ?
You can pick a set of sticks iff every pair of sticks does not meet. This gives the number of possible stick sets (without considering the convex polygon part) at most (15!)/(2^7 * 7!), which is about 2 million.
Now just backtrack and try every possible stick sets. The convex polygon part can be solved using triangle inequality.
Could you please explain how you arrived at that expression (15!)/(2^7 * 7!)
Each stick can be thought of as a corresponding to precisely one pair of points. Since we want the sticks not to intersect, this means the pairs must be distinct.
How many ways can we choose 7 distinct pairs from 15 vertices?
Choose the first pair, that can be done in 15C2 ways, then from the remaining 13, choose another 2, and so on. Multiplying these out, we get 15!/(2!)^7.
But note that the order of the 7 pairs themselves does not matter, so we have to divide by 7!.
Hope that helped.
Now that I think about it, the number of possible stick sets isn't bounded above by the said number, but the number of possible stick sets with size 7 is bounded by that number. Anyway, working with similar bounds shows that this approach can pass easily.
You can read about the author's analysis here. Sorry for the delay, we have been busy with regular work.