I want to say thanks to whom can help me to make this round: for testing pashka and cerealguy, for problems chavit and enot110 and andrewzta for supervising.
417A - Elimination. Author and realization Aksenov239.
The first thing, that you need to mention, is that if k ≤ n·m, then the answer is equal to 0. After that you need to take at least n·m - k people. There's three possibilities to do that:
- To consider only main rounds:
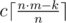 .
. - To take additional rounds to the number, which is divisible by n:
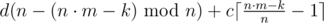 .
. - To take only rounds of the second type: d(n·m - k).
Also in this problem it is possible to write the solution, which check every possible combinations of the numbers of main and elimination rounds.
Solution: 6396283
417B - Crash. Author and realization Aksenov239.
Let us create array a with 105 elements, which is filled with - 1. In the cell a[k] we will contain the maximal number of the submissions of the participant with identifier k. We will process submissions in the given order. Let us process submission x k. If a[k] < x - 1, then the answer is NO, else we will update array a: a[k] = max(a[k], x).
Solution: 6396297
418A - Football. Author and realization Aksenov239.
Let's consider this tournir as graph. Each vertex should have out-degree k. Then the graph should contain exactly nk edges. But the full-graph contains 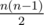 , because of that if n < 2k + 1 then the answer is - 1, otherwise we will connect the i-th vertex with i + 1, ..., i + k, taking modulo n if needed.
, because of that if n < 2k + 1 then the answer is - 1, otherwise we will connect the i-th vertex with i + 1, ..., i + k, taking modulo n if needed.
Solution: 6396331
418B - Cunning Gena. Author and realization Aksenov239.
Let us sort the friends by the number of the monitors in the increasing order. Afterwards we will calculate the dp on the masks: the minimal amount of money Gena should spend to solve some subset of problems, if we take first n friends. Then the answer we should compare with the answer for first i friends plus the number of the monitors, which the i-th friend needs. Is is not hard to see, that if we consider the friends in this order consequently, then we can recalc dp like in the knapsack problem. The running time of this algorithm is O(nlog(n) + n2m).
418C - Square Table. Author and realization Aksenov239.
Let's build array of the length n for each n, that the sum of the squares of its elements is the square:
- If n = 1, then take [1].
- If n = 2, then take [3, 4].
- If n is even, then take
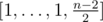 .
. - If n is odd, then take
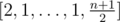 .
.
We are given two numbers n and m. Let array a corresponds to n, and array b corresponds to m. The we will build the answer array c as follows cij = ai·bj.
Solution: 6396358
418D - Big Problems for Organizers. Author chavit, realization Aksenov239.
This problem has two solutions.
The first one. Let's hang the tree on some vertex. Afterwards, let us calculate for eah vertex it's height and 3 most distant vertices in its subtree. Also let's calculate arrays for the lowest common ancestors problem. For each vertex i and the power of two 2j we have p[i][j], up[i][j] and down[i][j]:
- p[i][j] is the ancestor on the distance of 2j,
- up[i][j] is equal to the longest path from i to the vertices, which are situated in subtrees of the vertices on the path between i and p[i][j].
- down[i][j] is equal the same, but from the vertex p[i][j].
And the last part of this solution. Let us be given the query u v. Firstly, we find w = LCA(u, v). Afterwards, we need to find vertex hu, which is situated on the middle of the path between u and v. Really, we need to split the tree by this vertex, count the longest path from u in its tree and count the longest path from v in its tree. If we can imagine in the main tree, we can not delete this vertex, but with our precalculated arrays recalc this two values.
First solution: 6396376
The second solution. In a few words. Let's find the diameter of the tree. Precalc the answer for each vertices on the prefix. Then on the query we find two distant vertices on this diameter and the path. Obviously, diameter should contain the middle of the path, when we find it, using precalculated results on the prefixes and suffixes we can obtain the answer.
Second solution cerealguy: 6396390
418E - Tricky Password. Authors enot110, Aksenov239, realization Aksenov239.
The key theoretical idea of this problem is that the $2$nd row is exactly the same as the $4$th row, $3$rd row is exactly the same as $5$th row and so on. Because of that we need only to answer queries on the first three rows.
Let's move on to the practical part. In the first place we will compress coordinates, that any value will not exceed 2·105. Afterwards, let's split the array into parts of the length LEN. On each part we will calculate the following values: cnt[k] — the number of occurences of the number k on this prefix, also f[k] — the total number of the values, which occur exactly k times on this prefix. Array f we will store in the Fenwick data structure.
It is not hard to see, that array cnt contains the answer for the queries to the 2nd row. To get the answer for the queries to the 3rd row we need to calculate f[cnt[k]... 105]. Also it's quite understandable how to recalc this dp.
In summary, we will get 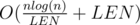 per query. And we take
per query. And we take 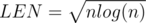 , then we will get
, then we will get 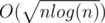 per query. Solution: 6396412
per query. Solution: 6396412













Nice editorial very good english!!
the problems in this contest are all very interesting.
How to solve div1C ??
Here's the trick: if an integer p can be written as the sum of the square of n integers, then p2 can also be written as the sum of the square of n integers. For example, if
then
Generally, if
then
So for an array of length $n$, how to make the sum of the square of its elements be a square of an integer? We can simply set a1 = ... = an = 1, and the array becomes {n - 2, 2, 2, ..., 2}. Then you can apply this method to generate the matrix.
yeah, from author's opinion, what we do is to generate n or m postive integers that the sum of their squares is also a square number.
How to solve div1-D? We have computed
p,downandup, what next?Problem Div1 E has a solution with complexity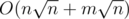 , just need to maintain two arrays sum1[n/Len][N], sum2[n/Len][N], where sum1[i][j] is the number of j in the first i*Len positions of row 1, and sum2[i][j] is the number of j in the first i*Len positions of row 2.
, just need to maintain two arrays sum1[n/Len][N], sum2[n/Len][N], where sum1[i][j] is the number of j in the first i*Len positions of row 1, and sum2[i][j] is the number of j in the first i*Len positions of row 2.
Can anybody please give bit more explanation about 418B — Cunning Gena? Thanks in advance
Consider we have dp[msk][last] = amount of min money spent on solving problems chosen on msk with hire maximum first last friends. (msk is bitmask of chosen problems)
Then suppose we want to hire the (last + 1)'s friend which cost is dp[msk][last] + cost[last + 1]. If this amount less than dp[msk|solve[last + 1]][last + 1], update it.
The answer is minimum of dp[allproblems][k] for all (1<=k<=N) plus cost of monitors required.
got it, Thanks!
But still, how do we know that optimal solution will be first k friends? why cannot it be, for example, first and fourth friends?
dont mind it
Strange explanation to problem div1 C. Do this, you will get accepted. No explanation , no proof, why this works. there is a comment regarding this problem but that's not also enough. seems like pure math :( . this is "Code"-forces not "math"-forces. Authors should send these kinds of problem in IMOs, not here.
I think that enough information is given to understand the solution. You have to think a little, but it is a nice thing to do.
For the first part, you can manually verify that the sum of the given values squared is a square. For the second part, note that if a12 + a22 + ... + an2 is a square, then (k·a1)2 + (k·a2)2 + ... + (k·an)2 is also a square.
Explanation of the idea how to make such arrays is simple. If you take first n - 1 nubmers such that the sum of their squares is odd, you should suppose it equals to some 2t + 1 and make last element equal to t. Then sum of all squares will be 2n + 1 + n2 = (n + 1)2.
thanks a lot for explaining!
P.S. i think editorial should have this idea too, not just the answer!
Thanks, now its clear to me. and I agree with JuanMata , the editorial should have this idea too, not just the answer!
Div1-D, second solution: "Let's find the diameter of the tree. (...) Then on the query we find two distant vertices on this diameter and the path. Obviously, diameter should contain the middle of the path," There are two possibilites: 1. I don't understand what author meant. 2. This is not true. One thing is for sure — I don't understand second sentence — what are "two distant vertices" ?? Which path is third sentence about? Obviously diameter doesn't have to contain middle of every path, so I guess author meant something else.
I think he meant "every maximal path goes through at least one node in the diameter".
It's not hard to see that a path that does not go through the diameter at least once cannot be maximal, because otherwise there would be a path bigger than the diameter.
In 417 A-Elimination, You've said: if k ≤ n·m, then the answer is equal to 0. I think it's: if n·m ≤ k, then the answer is equal to 0.
I just can't understand what 'realization' means...
implementation
54416306 why tle I think n^2 complexity should work for problem 417C/418A according to constrains given
Heres your accepted code . https://codeforces.com/contest/418/submission/54417725
thanks
I just wanna know the name of the fucker who is putting tags in the problem and putted
dp 1500tag in problem A (Elimination).Could anyone explain me problem A. Very poor statements.