First I want you to read the task and try to solve it in linear time complexity, and minimum memorize complexity.
Lonely Integer
There are N integers in an array A. All but one integer occurs in pairs. Your task is to find out the number that occurs only once.
Input Format
The first line of the input contains an integer N indicating number of integers in the array A. The next line contains N integers each separated by a single space. Constraints 1 <= N < 100 N % 2 = 1 ( N is an odd number ) 0 <= A[i] <= 100, ∀ i ∈ [1, N]
Output Format
Output S, the number that occurs only once.
Sample Input
3
1 1 2
Sample Output
2
If you don't have any idea I will write a code.
#include <cmath>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
int N;
cin >> N;
int tmp, result = 0;
for (int i = 0; i < N; i++) {
cin >> tmp;
result ^= tmp;
}
cout << result;
return 0;
}
Cool trick using only xor operation, but I can't prove why that work. Can anyone prove it?











http://codeforces.com/blog/entry/12534
Same proof with this.
x xor x = 0So xor all numbers. If a number is xor twice, number doesn't change anything.http://www.spoj.com/problems/OLOLO/
The proof follows from properties of xor:
a^b=b^aa^a=0a^0=aThe first one lets us reorder the numbers in any way without the xor being affected. Then, we get the xor as
(a^a)^(b^b)^(c^c)^...^(r^r)^s, which is0^0^0^...^0^s=s.Also, the linear time complexity is caused by computers being constructed to do bitwise operations in O(1). If you did it on paper, your complexity would be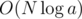 . It's a cool trick nevertheless.
. It's a cool trick nevertheless.
Actually for reodering numbers we need one more property:
a^(b^c)=(a^b)^c.