I'll upload my example solutions and will post links to them as soon as it becomes possible.
Some of the problems editorials contain an additional challenge which is apparently harder to comprehend than the original problem. Feel free to share and discuss your ideas in the comments. =)
If we add 1 to a number, its binary representation changes in a simple way: all the least significant 1's change to 0's, and the single following 0 changes to 1. It suffices to find the length of largest suffix which contains only 1's, suppose its length is l. Then the answer is l + 1 except for the case when all the string consists of 1, when the answer is l.
It is amusing that div1E problem is concerned with addition of 1 to a binary integer as well. =)
Optimal strategy is as follows: for every segment of consecutive 1's open the first letter in segment, scroll until the last letter in segment, if there are more unread letters left, return to list.
It is easy to show that we can not do any better: observe the moment we read the last letter from some segment of consecutive 1's. There are no adjacent unread letters now, so we either have to scroll to some read letter or return to list of letters, either way we make an operation which does not result in reading an unread letter, so every segment (except for the last) must yield at least one such operation.
If string s contains a non-trivial palindromic substring w, then it must contain palindromic substring of length 2 or 3 (for instance, center of w). Therefore the string is tolerable iff no adjacent symbols or symbols at distance 1 are equal.
Now for the lexicographically next tolerable string t. t is greater than s, so they have common prefix of some size (maybe zero) and the next symbol is greater in t than in s. This symbol should be as right as possible to obtain minimal possible t. For some position i we can try to increment si and ensure it's not equal to si - 1 or si - 2. If we find some way to do this, the suffix can always be filled correctly if only p ≥ 3, as at most two symbols are forbidden at every moment. Every symbol from suffix should be as small as possible not to make conflicts. So, a greedy procedure or some kind of clever brute-force can be implemented to solve the problem in O(n). Cases p = 1 or 2 are easy, as only strings of length at most 1, and at most 2 respectively fit.
This is an application on general approach to generate next lexicographical something: try to increment rightmost position so that suffix can be filled up in some way, then fill the suffix in least possible way.
As pointed out in Russian discussion, this problem is a simplified version of the problem from some previous round: 196D - The Next Good String. We were not aware of this and apologize for the misfortune. Luckily, no copied solutions from that problem were spotted. If you enjoyed this simple version, you may want to try the harder one know. =)
There are several ways to solve this problem. We'll describe the most straightforward one: we can generate all possible permutations of coordinates of every point and for every combination check whether given point configuration form a cube. However, number of configurations can go up to (3!)8 > 106, so checking should work quite fast.
One way to check if the points form a cube is such: find minimal distance between all pairs of points, it should be equal to the side length l. Every vertex should have exactly three other points at distance l, and all three edges should be pairwise perpendicular. If these condition are met at every point, then configuration is a cube as there is no way to construct another configuration with these properties. This procedure performs roughly 82 operations for every check, which is fast enough. There are even more efficient ways of cube checking exploiting various properties of cube.
There are various optimizations to ensure you fit into time limit. For instance, applying the same permutation to coordinates of all points keeps every property of the cube, therefore we can fix order of coordinates for one point and permute all other. This single trick speeds up the algorithm 6 times, which allows some less efficient programs to be accepted.
A challenge: apparently, checking may be done as follows: find the length side l, then count number of pairs on distance l, 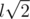 ,
, 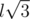 . A cube must contain exactly 12 pairs of first kind, 12 pairs of second kind and 4 pairs of third kind. Can you prove that this condition is sufficient for configuration to form a cube? Is it true if we allow points to have non-integer coordinates? Can you propose an even easier algorithm for checking?
. A cube must contain exactly 12 pairs of first kind, 12 pairs of second kind and 4 pairs of third kind. Can you prove that this condition is sufficient for configuration to form a cube? Is it true if we allow points to have non-integer coordinates? Can you propose an even easier algorithm for checking?
It is quite diffcult to store the whole string after each query as its length grows exponentially and queries may change it dramatically. The good advice is: if you can't come up with a solution for a problem, try solving it from the other end. =)
Suppose we know for some sequence of queries that digit d will turn into string td for every digit. Then string s = d1... dn will turn into td1 + ... + tdn (+ for concatenation). Denote v(s) numeric value of s. Then v(s) can be expressed as v(tdn) + 10|dn|(v(tdn - 1) + 10|dn - 1|(...)). So v(s) can be computed if we know md = v(td) and sd = 10|td| for all d. As we need answer modulo P = 109 + 7 we can store these numbers modulo P.
Now prepend some new query di → ti to given sequence. How will md and sd change? Clearly, for all d ≠ di these numbers won't change, and for di they can be computed according to the rule above. This recounting is done in O(|ti|) time. After adding all queries, find answer for s using the same procedure in O(|s|) time. Finally, our time complexity is 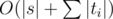 . The code for this problem pretty much consists of the above formula, so implementation is as easy as it gets once you grasp the idea. =)
. The code for this problem pretty much consists of the above formula, so implementation is as easy as it gets once you grasp the idea. =)
Optimized simple solutions which just replaced substrings could manage to pass pretests. Sorry for that.
A challenge: this problem has a natural modification when you have to give an answer after each query. Using algorithm described above it can be solved offline in O(n2) time. Can we do better than this? What if we are limited to answer online?
This problem required some skill at probabilities handling, but other than that it's quite simple too.
Denote number of earned coins as X, and number of earned coins from selling items of type i as Xi. Clearly X = X1 + ... + Xk, and EX = EX1 + ... + EXk (here EX is expectation of X). As all types have equal probability of appearance, all Xi are equal, so EX = kEX1. Now to find EX1.
If we look only at the items of one type, say, 1, items generation looks like this: with probability  we get nothing, and with probability
we get nothing, and with probability 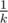 we get out item with level distributed as usual. Denote dn, t expectation of earned money after killing n monsters if we have an item of level t at the start. Clearly, d0, t = 0 (we have no opportunity to earn any money), and
we get out item with level distributed as usual. Denote dn, t expectation of earned money after killing n monsters if we have an item of level t at the start. Clearly, d0, t = 0 (we have no opportunity to earn any money), and 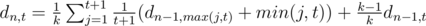 , which is equal to
, which is equal to 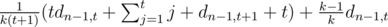 =
=  . To get the answer note that EX1 = dn, 1. The sad note is that this DP has Ω(n2) states, which is too much for
. To get the answer note that EX1 = dn, 1. The sad note is that this DP has Ω(n2) states, which is too much for 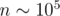 .
.
Maybe if we cut off some extremely-low-probability cases we can do better? For instance, it is clear that probability of upgrading an item descreases with its level, so apparently it does not get very high. We know that expected number of tries before first happening of event with probability p in a series of similar independent events is 1 / p. Therefore, expected number of monsters we have to kill to get item of level T is 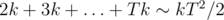 . So, in common case our level can get up to about
. So, in common case our level can get up to about 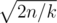 , which does not exceed 500 in our limitations. We would want to set such bound B that ignoring cases with t > B would not influence our answer too much. That can be done with rigorous bounding of variance of T and applying some bounding theorem, or with an empirical method: if we increase the bound and the answer doesn't visibly change, then this bound is fine. It turns out B ≥ 700 is good enough for achieving demanded precision. Thus solution with
, which does not exceed 500 in our limitations. We would want to set such bound B that ignoring cases with t > B would not influence our answer too much. That can be done with rigorous bounding of variance of T and applying some bounding theorem, or with an empirical method: if we increase the bound and the answer doesn't visibly change, then this bound is fine. It turns out B ≥ 700 is good enough for achieving demanded precision. Thus solution with 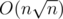 complexity is obtained (here we assert that
complexity is obtained (here we assert that 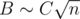 , and constant C is buried in the big O).
, and constant C is buried in the big O).
A challenge: suppose we have the same rules of killing monsters and obtaining items, but now we are free to choose whether to sell a new item or an old one. We act so that to maximize our number of coins in the end. What is the expected number of coins if we act optimally?
Now it is sometimes more profitable to sell a powerful item, but sometimes it isn't. How fast a solution can you come up with?
This seems to be a simple graph exercise, but the problem is with enormous weights of paths which we need to count and compare with absolute precision to get Dijkstra working. How do we do that?
The fact that every edge weight is a power of two gives an idea that we can store binary representation of path value as it doesn't change much after appending one edge. However, storing representations explicitly for all vertices is too costly: the total number of 1's in them can reach Ω(nd) (d is for maximal xi), which doesn't fit into memory even with bit compression woodoo magic.
An advanced data structure is needed here which is efficient in both time and memory. The good choice is a persistent segment tree storing bit representation. Persistent segment tree is pretty much like the usual segment tree, except that when we want to change the state of some node we instead create a new node with links to children of old node. This way we have some sort of ''version control'' over tree: every old node is present and available for requests as its subtree can never change. Moreover, all queries are still processed in  time, but can create up to
time, but can create up to  new nodes.
new nodes.
What queries do we need? Adding 2x to binary number can be implemented as finding nearest most significant 0 to x-th bit, setting it to 1 and assigning 0's to all the positions in between. Usual segment tree with lazy propagation can do it, so persistent tree is able to do it as well.
Comparing two numbers can be done as follows: find the most singificant bit which differs in two numbers, then number with 0 in this bit is smaller; if no bits differ, then numbers are clearly equal. That can be done in  if we store hashes of some sort in every node and perform a parallel binary search on both trees. Time and memory limits were very generous so you could store as many different hashes as you wanted to avoid collisions.
if we store hashes of some sort in every node and perform a parallel binary search on both trees. Time and memory limits were very generous so you could store as many different hashes as you wanted to avoid collisions.
That concludes the general idea. Now we use this implementation of numbers as a black-box for Dijkstra algorithm. Every operation on numbers is now slowed by a factor of 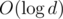 , so our solution has
, so our solution has 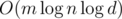 complexity. However, great caution is needed to achieve a practical solution.
complexity. However, great caution is needed to achieve a practical solution.
First of all, in clueless implementation comparison of two "numbers" may require 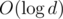 additional memory as we must perform "push" operation as we descend.
additional memory as we must perform "push" operation as we descend. 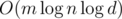 memory is too much to fit even in our generous ML. There are plenty of ways to avoid this, for instance, if we want to push the value from node to children, we actually know that the whole segment consists of equal values and can answer the query right away.
memory is too much to fit even in our generous ML. There are plenty of ways to avoid this, for instance, if we want to push the value from node to children, we actually know that the whole segment consists of equal values and can answer the query right away.
I would like to describe a clever trick which optimizes both time and memory greatly and also simplifies implementation. It allows to get rid of lazy propagation completely. Here it comes: initially build two trees containing only 0's and only 1's respectively. Now suppose we want to assign some value (0, for instance) on a segment and some tree node completely lies inside of query segment. Instead of creating a new node with a propagation mark, we can replace the node with corresponding node from tree filled with 0. This way only  new nodes are created on every query (which is impossible to achieve with any kind of propagation which would require at least
new nodes are created on every query (which is impossible to achieve with any kind of propagation which would require at least 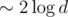 ), and also nodes need to store less information and become lighter this way. Also, no "push" procedure is required now.
), and also nodes need to store less information and become lighter this way. Also, no "push" procedure is required now.
No challenges for this problem as it is challenging enough itself. =) Implementing this problem is a great exercise for anyone who wants to become familiar with complicated structures and their applications, so solving it in the archive is advisable.
That's pretty much it. If there are still questions, you may ask them in the comments. Thanks for reading!










What's the greedy approach to solve 464A - Нет палиндромам!?
Round #265 was my first contest here at Codeforces and I enjoyed very much participating in it, in a large part due to the varied analytic approaches considering all problems. The contest's problemset at Div. 2 didn't demand pulling off very advanced algorithms but, first of all, some careful observation and coding in a straighforward manner so that the round time would be well spent.
I thought that clearing problem D, even instead of its easier conterparts B and C, would fit in a reasonable round strategy since checking its entire search space for solution correctness is straightforward. However, I had a more of a hard problem trying to fit my Java solution under a doable time limit and I also took too much time modifying my solution's code in place of the algorithm itself, so had I opted for an "easy" algorithm speed-up such decision would pay off dearly.
464A — No to Palindromes's editorial is not detailed enough. there are two things to be done: 1. keep palindrome 2. next minimal string t the first thing, the editorial says just keep checking t[i] != t[i — 1] && t[i] != t[i — 2], that's ok. but the second thing and the whole process is not clear enough. can someone explain it more clearly?
let's look at the a little bit changed last example given in the problem:
n = 4, p = 4, s = bacdif we want to find lexicographically next string we should start to change right most char (d). but it can't changed because p = 4 and we can just use a, b, c, d. so we try to change the char at the left of the right most char (c). we increase it and we get d and we delete all of the chars that comes after this char and we get:bad_after this we try to fill the deleted part of the string with a string that is as possible as lexicographically small. so we try to put a and we get:badathis is not a valid string because "ada" is palindrome. lets try b:badbyes we found.i hope this will help.
And also for filling the deleted part,on average you need O(n) time,because for every j from i+1 to n,you want to put the lowest letter != s[j-1] and != s[j-2],and this will take at most 3 steps. :) This is why the total complexity is O(n^2 * 26).
excellent
can someone provide a better explanation to 464C — Substitutes in Number ?
There are two things we need to keep track of for each digit: the value it will eventually turn into, which we can keep modulo 10^9+7, and the length of the number. With just these two values, we can apply rules efficiently. Keep track of these in two arrays val, len
Our base case is just that each digit goes to itself and has length 1. (i.e. val[i] = i, len[i] = 1).
Now, let's focus on applying a single rule of the form p -> d_1d_2...d_n
Notice applying these rules takes time linear to the number of characters in the rule, so applying all rules will take O(|t|) time.
Now, apply rules from the end of list to the front of the list until we get to the first rule. To get the final answer, just add a rule 0->s to the front, and return val[0]. Total running time is O(|s|+|t|).
You need to be careful with mods, but you can also notice you should mod the lengths of numbers by (10^9+6) since we're taking 10^len, and we know 10^len mod 10^9+7 = 10^(len mod 10^9+6) mod 10^9+7 by Fermat's little theorem. Of course, instead of storing len, you can just store 10^len directly, and you can adjust the rules and base case above as necessary. This way doesn't require FLT, and is what the editorial is referring to.
Hopefully this helps, this is a brief overview on how to solve.
Why do we need to process the queries backward from the end to the front? UPD: Sorry for a naive question, I got it!. Your explanation is clear for me now!
thanks :)
can u help me find why my submission return a TLE. thank u.http://codeforces.com/contest/465/submission/7749873
Source of TL (if it was not TL, it would be WA):
gets stuck in infinite loop, when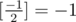 .
.
expis negative, becauseYour problem is next:
len[i]can grow exponentially, so if you are not careful, it will overflow long long type, and probably will be negative at some point.But because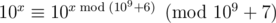 (see Fermat's little theorem), you can store
(see Fermat's little theorem), you can store
len[i]modulo 109 + 6: 7750490. Only change is lineu r right!thank u!
thanks a lot! :)
hi can u debug my code for poblem E.
It is failing on test case 10.
(https://codeforces.com/contest/464/submission/219417850)
219417850
In the constraints, you can see that ~~~~~ Xi <= 100'000 ~~~~~
So, when Xi is bigger than, lets say, 64, the weight of the edge would overflow (int overflow) so your code won't show the right results on the comparison test (in the priority queue). You should implement a persistent tree to do this efficiently.
It seems like there is a typo in the explanation of the Div2.E/Div1.C.
The resulting number is written to be represented as
v(tdn) + 10^|dn|*(v(tdn - 1) + 10^|dn-1|*(...)), however, it seems like it must bev(tdn) + 10^|tdn|*(v(tdn-1) + 10^|tdn-1|*(...)).For example, lets
s=01initial string, if substitutions are0->23and1->45, then the resulting string iss=2345, according to the formulav(s) = 45 + 10^|1|*23which is incorrect.Did anyone manage to get an AC in the problem 464B — Restore the cube by coding in Java?
I implemented the brute force approach mentioned in the editorial in Java but got a TLE: Java Solution
Any ideas on speeding up the solution?
Have you tried not to shuffle first point?
I haven't but I can. Could you please explain in more detail the correctness of the solution if the first point is not shuffled?
Suppose you found a cube. Shuffle coordinates of all points in the same way so that first point will stay the same. Cube will be still a cube because coordinates are independent.
I tried your suggestion, but sadly I get a WA: Modified Java submission
Although, I get the correct answer with my previous code. Am I doing something wrong?
Hi Alex, I figured out the mistake in my code. I managed to get an AC after keeping the first point constant. Thanks a lot!
AC Solution
Hi sultan, I am still not able to figure out why we need to fix one point and shuffle only others.
Could you please help me understanding that?
Hi, we can fix one point and find the other points by shuffling. If a cube is possible then we'll know, no need to shuffle the fixed point.
To fully understand this, I think it'll help if you visualize/draw the figures on paper.
The way I understood it was by reducing the 3d cube to a 2d rectangle. Take any rectangle in the 2d plane, start with axis parallel rectangles. Now keep one point fixed. Swap (x,y) coordinates of the rest of the 3 vertices. You'll again get a rectangle of the same length and breadth. Go ahead, draw it on paper and see for yourself.
Similar concept can be applied to the 3d cube, when we ensure that the coordinates are shuffled in the same way i.e. for e.g. swap x and y of all vertices except one, the resulting 3d figure will still be a cube of the same dimensions. Similarly, it holds true if you swap y and z, z and x, etc
I hope I was clear enough :)
464E — The Classic Problem
Memory problem can be avoided by keeping 32 bits in leaf node. Then no other tricks are needed, and you can add 2^x brutally (add 2^x to the corresponding leaf node, if it overflows add 1 to the next leaf node and so on).
We can also have perfect hashing by numbering vertices like in checking tree isomorphism.
Solution
Not true, this can result in quadratic complexity, for example your code with test generator on ideone.
The idea of test: the graph is a tree that consists of
i.e. edge
i.e. edge
Find the shortest path from 1 to 100'000.
Here, updating the shortest path to the vertices with numbers from 50 001 to 99 999, you will perform 50 000 adds of 2x for every vertex.
That's right, my mistake, thanks.
why can't it be solved by kruskal?
In problem A I forgot that the given string didn't contain palindroms and still get AC. The algorithm does the following:
Iterate from i=0...size(s)-1
a. Check if s[i]==s[i+2], if yes:
--> s= next substring s[0...i+2] (so p=3 a c b c a a c c a a)
a c c a a)
--> go back to the earliest position modified by the update-2.
b. else check if s[i]==s[i+1], if yes do sth analogous.
Do you think tests weak, that the condition could be removed or that the condition makes my algorithm run in time?
Thanks!
WARNING: I'm new to probability theory, so my post may not be the smartest post here, but I'm curious:
In div1 D (464D - World of Darkraft - 2), why can't the Coupon Collector's Problem be applied?
EDIT: I realize now that probably it doesn't apply, as the expectations are not independent (probability of getting level X depends on probability of getting X - 1)
464B — Restore Cube , In the editorial , it is written "Is it true if we allow points to have non-integer coordinates?".
What does he mean by this? I am getting WA on test case 15 ( it contains a lot of negative integers ). Here is the link to my code ( in java ) : http://codeforces.com/contest/465/submission/7737985 Can anyone help ??? Thanks in advance.
i am quite confused about the The Classic Problem,since it too strange for the modify and push
464E - Классическая задача
TL&DR: The tests are not complete.
In this problem when adding bits to large numbers instead of searching for the closest 0 to the left I relied on ripple carry and the fact that it's amortized O(1).
You might notice that amortized complexity usually doesn't work for persistent data structures so my solution is supposed to be quadratic. However, the existing tests do not reveal this problem.
Here is a test generator that kills my initial solution (7789804):
Fortunately, there is a trick that lets you recover the amortized O(1) (7789945). Unfortunately this trick doesn't improve your time on Codeforces.
But ripple carry is amortized when you accumulatively keep incrementing the same number but in this problem you might need to increment the same number by the same amount, i.e. do exactly the same operation, many times and then your cost is not amortised. Unless maybe you do some sort of caching--is this what your "trick" is? And did I describe the same reason for which you think your initial solution is supposed to be quadratic?
Can someone please tell me why I am getting Runtime Error using this code: http://ideone.com/8m5Bve Problem is C. Substitutes in Number. Codeforces Round #265 (Div. 1)
Can someone provide a prove for those conditions in 464B — Restore Cube will form a cube and not the different thing?
Is there a solution for the challenge part of 464C — Substitutes in Number?
If someone could comment on a possible solution to the challenge part of 464C, that would be great!
464E — The Classic Problem
Why do you need a tree containing only 1's? I used your "clever trick", which I like, but I only needed a tree containing only 0's.
can anyone please clear my doubt in
464A No to Palindrome? Suppose we find a position 'i', and increase the corresponding char s[i] such that s[i] != s[i-1] and s[i] != s[i-2]. Now consider the prefix s[0:i+1]. How can you guarantee/prove that there exists a tolerable string with s[0:i+1] as its prefix ?Endagorion ?