Keeping track of both Codeforces round and online team contest was a doozy, so this is only the best draft of the editorial I have. Missing problems will gradually be added, and existing explanations may improve over time. Hope you enjoyed the problems, and let me know if anything can be explained better!
UPD: okay, all of the problems are out, and most of the bugs are fixed (I hope). By the way, we had a nice discussion with Errichto on his stream about Div. 2 problems, which some of you may find more approachable. Be sure to check it out, as well as other stuff Errichto creates!
(Kudos to Golovanov399 for his neat grid drawing tool)














 in the sense that no character occurs more times in
in the sense that no character occurs more times in 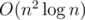 time if we sort the tuples and compare only the adjacent pairs,
time if we sort the tuples and compare only the adjacent pairs, time if we hash the tuples beforehand using the
time if we hash the tuples beforehand using the 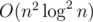 , or
, or  .
.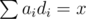 with high precision, and then make alterations to it so that the balance is decided on
with high precision, and then make alterations to it so that the balance is decided on 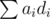 will be changed by the value of
will be changed by the value of 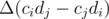 , which has the same sign as
, which has the same sign as 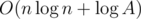 queries, in practice this number is about 450 on the present constraints.
queries, in practice this number is about 450 on the present constraints.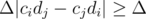 away from
away from 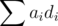 changes ever so slightly when add practically zero number to it, so that it can dance around
changes ever so slightly when add practically zero number to it, so that it can dance around  queries, where
queries, where  .
.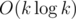 time.
time.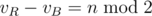 . It follows that the equivalent game would be to minimize
. It follows that the equivalent game would be to minimize 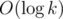 .
.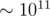 battles). How can we optimize that? Let us find
battles). How can we optimize that? Let us find 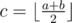 . If
. If 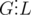 . It can also be shown that
. It can also be shown that 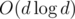 time for a vertex with
time for a vertex with 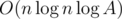 , where
, where 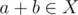 . Let's arrange them in a table, roughly like this (second sample, O stands for possible value, . for impossible):
. Let's arrange them in a table, roughly like this (second sample, O stands for possible value, . for impossible):
