Given an equation like this:
The general solution to such an equation is 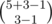 .
.
Where did that come from, basically to solve the previous equation we re-model it into another equivalent type of easily solvable combinatorics problem which is counting the number of possible arrangements for the following string "0011111" the answer for this is 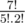 which is equal
which is equal 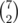 which is equal to number of solutions to the equation, how did this happen, we say that the "1"s represent the answer of the equation and the "0"s represent the number of variables -1, let's clear that a bit,
which is equal to number of solutions to the equation, how did this happen, we say that the "1"s represent the answer of the equation and the "0"s represent the number of variables -1, let's clear that a bit,
for a string like that "0011111" this means x1 = 0, x2 = 0, x3 = 5,
another string like that "1101011" means x1 = 2, x2 = 1, x3 = 2,
lastly a string "1111100" means x1 = 5, x2 = 0, x3 = 0.
So you see that the answer of the number of arrangements of the string is actually the answer of the number of integral solutions of the equation. The general solution to the equation
is 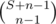 , where n number of variables and S the summation of the variables.
, where n number of variables and S the summation of the variables.
Side note, this happens a lot in combinatorics where we look for another much easier problem having the same answer to the problem we are facing.
Back to our problem now we have the answer to the equation, but let's make it a bit harder what if there were some constrains on our equation, for instance:
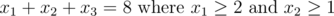
Here we can return to our original problem by doing a very simple trick which is subtracting the limits from the answer of the equation, at our example the solution of the equation is 8 and we want to satisfy our constrains, so we say that we will take the the constrains and subtract them from the answer as if we make the variables start again from zero and again, we solve the problem that we had solved before. So to formalize the last part we say if we have the following equation:
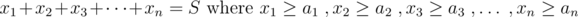
The solution to such problem is:
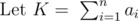
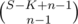
As you can see it is similar to the previous solution but we have added the K term to it, and of course if there is no constrain on a certain variable you can put its constrain variable equal to zero.
Now we have solved the equation if such an xi ≥ ai, but what if we have another constrain like this xi < ai the only way to solve this(or the only way I know) is to solve it using complement technique, where we reverse the constrain and get all possible solutions and subtract it from the complement. Let's clear with an example:
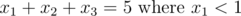
It's hard to get the answer with the given constrain but it is easy to get it's complement which is x1 ≥ 1 which is a problem like the previous one and can be solved easily which will be 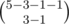 so that is the solution to the complement, now to get the solution to the normal constrain we subtract the complement from the total that will be
so that is the solution to the complement, now to get the solution to the normal constrain we subtract the complement from the total that will be
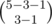 —
— 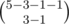
But now what if we have this equation:
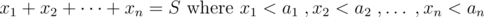
We use the same complement technique but this time we have to use inclusion and exclusion principle, let's clarify this a bit:
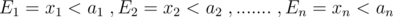
we have to get their intersection 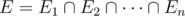 but that is hard, but we can get the complement easily
but that is hard, but we can get the complement easily
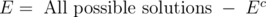
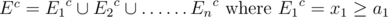
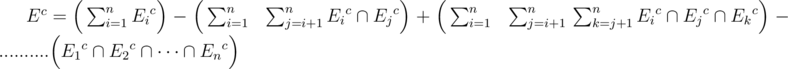
After seeing the previous Ec how can we program such a thing, we can code it using bit-masking where we can represent the 1 bits as the sets that are going to intersect, if the number of sets that are intersecting are odd then we add that intersection else we subtract it.
As you can see using bit-masking will only allow us to work while n ≤ 20.
Moving to a practical problem that we can re-model it as a linear equation is this problem 451E - Devu and Flowers . We can say that every box represents a variable in our linear equation and the number of flowers in each box is the constrain that we cannot exceed.
Any constructive reviews will be appreciated, if there is any unclear part please mention it.











What if the constraints are like x2 is even or multiple of 3. I mean no. of solution of x + y + 2z = S etc;
You can always use dynamic programming and solve the problem in O(Sn) time.
Could You explain about it. I am new to programming and I could understand the coin change problem related to this But I could solve on my own. Can You provide a better explanation>>
If you know number of solutions a(T) of y + 2z = T for T <= S, you can find the number of solutions b(T) of x + y + 2z = T for T <= S: b(T) = a(T) + a(T — 1) + ... + a(0).
In its general form, generating functions are used.