471A - MUH and Sticks
Given six sticks and their lengths we need to decide whether we can make an elephant or a bear using those sticks. The only common requirement for both animals is that four leg-sticks should have same length. This means that the answer "Alien" should be given only if we can't find four sticks for the legs. Otherwise we will be able to make some animal. The type of the animal will depend on the relation of the remaining sticks' lengths. If they are equal then it will an elephant, if they are different we will have a bear.
So this algorithm should solve the problem:
Find the number which appears at least four times in the input.
If no such number exist then the answer is "Alien".
Otherwise remove four entries of that number from the input.
After removing that number you will have two numbers left, compare them and decide whether it's an elephant or a bear.
One shortcut for this problem might be to sort the input array, then if it's a bear or an elephant then 3rd and 4th elements in the sorted should be animal's legs. So you can assume that one of these numbers is the length of the leg and count how many times you see this number in the input.
Author's solution: 7977022
Since the numbers in the input are very small you can implement 'brute force' solution as well. By brute force solution in this case I mean that you can actually check all possible values for leg-length, head-length and body-length. If in total they give the same set as the input then you found a matching, all you need is to check whether it's a bear or an elephant. And it's an alien if you checked all possible combinations and found nothing matching to the input. Though in this case the brute force solution is not easier than another one.
Checking all possible lengths solution: 7975645
It seems that there were two common mistakes people were making in this problem:
Not taking into account that legs can be of the same length as body or head. So you can't just count the number of distinct numbers in the input to decide which type of animal is that. We assumed that people might make such a mistake, there was a relevant warning in the statement.
Trying to sort the input and then check whether some elements in this array are equal to other elements and based on this comparison decide which type of animal is that. People were simply making mistakes when deciding which elements to compare. The correct way to implement this is:
// 0-indexing below, array is assumed to be sorted
if (l[0] == l[3]) cout << (l[4] == l[5] ? "Elephant" : "Bear");
else if (l[1] == l[4]) cout << "Bear";
else if (l[2] == l[5]) cout << (l[0] == l[1] ? "Elephant" : "Bear");
else cout << "Alien";
Solution: 7977214
This solution seems to be shorter but there are many failed solutions like this because people were not paying enough attention to the details. So I would prefer implementing more straightforward approach.
Hope you liked the pictures!
471B - MUH and Important Things
You need to check whether exist three pairwise different permutations of the indices of the input which result in array being sorted. Generally you can count the number of total permutation which give non-decreasing array. This number might be very large and it might easily overflow even long integer type. And what is more important is that you don't actually need to count the exact number of such permutations.
Let's tackle this problem from another angle. Assume you already sorted the input array and you have the corresponding permutation of indices. This already gives you one array for the result, you only need to find two more. Let's look for any pair of equal numbers in the input array, if we swap them then we will get another valid permutation. And if we find one more pair of equal numbers then swapping them you can get third permutation and that will be the answer. You need to keep in mind here that one of the indices when swapping the second time might be the same as one of the numbers in the first swap, that's ok as soon as second index is different. So all you need to do is to find two pairs of indices which point to the equal elements.
The entire algorithm is as follows:
Transform the input array into array of pairs (tuples), first element of the pair will be the number given in the input array, the second element will be the index of that number.
Sort that array of pairs by the first element of the pairs. Then the second elements will give you one correct permutation.
Scan this array in order to find possible swaps. You just iterate over this array and check if the first element in the current pair equals to the first element of the previous pair. If it equals you remember the indices of these two pairs. You stop scanning the array as soon as you have two swaps.
Then you check how many swaps you have, if you have less than two swaps then there are no three distinct permutations.
Otherwise you have two swaps which means that you have an answer. So you print the current permutation, then you execute the first swap (you just swap those two elements you remembered in the first swap), then you print the permutation array received after executing that swap. And you execute the second swap and print the permutation array third time.
Author's solution: 7977528
471C - MUH and House of Cards
Card house. This problem required some maths, but just a little bit. So in order to start here let's first observe that the number of cards you need to use for a complete floor with R rooms equals to:
C = Crooms + Cceiling = 2·R + (R - 1) = 3·R - 1
Then if you have F floors with Ri rooms on the i-th floor then the total number of cards would be:
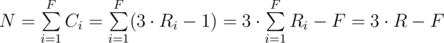
where R is the total number of the rooms in the card house.
This already gives you an important property — if you divide N + F on 3 then the remainder of this division should be 0. This means that if you have found some minimum value of floors somehow and you found maximum possible number of floors in the house, then within that interval only every third number will be a part of the solution, the rest of the numbers will give a non-zero remainder in the equation above.
Now let's think what is the highest house we can build using N cards. In order to build the highest possible house obviously you need to put as few cards on each floor as you can. But we have a restriction that every floor should have less rooms than the floor below. This gives us the following strategy to maximize the height of the house: we put 1 room on the top floor, then 2 rooms on the floor below, then 3 rooms on the next floor, etc. In total then the number of cards we will need equals to:
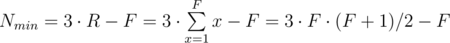
This is minimum number of cards we need in order to build a house with F floors. This gives us a way to calculate the maximum height of the house we can build using N cards, we just need to find maximum F which gives Nmin < = N. Mathematicians would probably solve the quadratic inequation, programmers have two options:
Check all possible F until you hit that upper bound. Since Nmin grows quadratically with F then you will need to check only up to
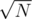 numbers. This gives
numbers. This gives 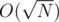 time complexity and fits nicely in the given time limit.
time complexity and fits nicely in the given time limit.The second approach would be a binary search. Using binary search to find maximum number of the floors would give you O(logN) time complexity. This was the intended originally solution but it was decided to lower the constraints in order to allow sqrt solutions as well.
Now that you know the maximum number of the floors in the house you might need to correct it a bit because of that remainder thing we discussed above, this might make your maximum height one or two floors lower. Looking again at the remainder discussion on top we can see that starting from here only every third number will be valid for an answer. Now you can either count them brutally (back to 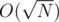 solution) or you can simply calculate them using this formulae:
solution) or you can simply calculate them using this formulae:
ans = (Fmax + 3 - 1) / 3 (integer division)
That seems to be it, just don't forget to use longs all the time in this problem.
Author's O(logN) solution: 7977863
Authors 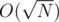 solution: 7977888
solution: 7977888
471D - MUH and Cube Walls
In this problem we are given two arrays of integers and we need to find how many times we can see second array as a subarray in the first array if we can add some arbitrary constant value to every element of the second array. Let's call these arrays a and b. As many people noticed or knew in advance this problem can be solved easily if we introduce difference arrays like that:
aDiffi = ai - ai + 1 (for every i = = 0..n - 1)
If we do that with both input arrays we will receive two arrays both of which have one element less than original arrays. Then with these arrays the problem simply becomes the word search problem (though with possibly huge alphabet). This can be solved using your favourite string data structure or algorithm. Originally it was intended to look for linear solution but then we made time limit higher in case if somebody will decide to send O(NlogN) solution. I haven't seen such solutions (that is understandable) but some people tried to squeeze in a quadratic solution.
Linear solution can be made using Z-function or KMP algorithm. In order to add a logarithmic factor you can exercise with suffix array for example. I had suffix array solution as well, but it's a lot messier than linear solution.
There is one corner case you need to consider — when Horace's wall contains only one tower, then it matches bears' wall in every tower so the answer is n. Though for some algorithms it might not even be a corner case if you assume that empty string matches everywhere. Another error which several people did was to use actual string data structures to solve this problem, so they converted the differences to chars. This doesn't work since char can't hold the entire range an integer type can hold.
I didn't think that switching to difference arrays will be that obvious or well-known, so I didn't expect that this problem will be solved by that many people.
Author's Z-function O(n + w) solution: 7978022
Author's suffix array O((n + w)·log(n + w)) solution: 7978033
471E - MUH and Lots and Lots of Segments
Given a set of horizontal/vertical lines you need to erase some parts of the lines or some lines completely in order to receive single connected drawing with no cycles.
First of all let's go through naive N2 solution which won't even remove cycles. In order to solve this problem you will need a DSU data structure, you put all your lines there and then for every pair of horizontal and vertical line you check if they intersect and if they do you join them in DSU. Also your DSU should hold the sum of the lengths of the joined lines. Initially it should be equal to the line lengths. Since there might be up to N2 / 4 intersections between lines we receive a quadratic solution.
Now let's get rid of cycles. Having the previous solution we can do it pretty easily, all we need is to change the way we were connecting the sets in DSU if some lines intersect. Previously we were simply asking DSU to join them even if they already belong to the same set. Now what we will do is when finding some pair of lines which intersects and is already joined in DSU instead of asking DSU to join them again we will ask DSU to decrement their length sum. In terms of the problem it is equivalent to erasing a unit piece of segment in the place where these two lines intersect and this will break the cycle. With this change we already have a correct solution which is too slow to pass the time limits.
Now we need to make our solution work faster. We still might have up to N2 / 4 intersections so obviously if we want to have a faster solution we can't afford to process intersections one by one, we need to process them in batches. All our lines are horizontal and vertical only, so let's do a sweep line, this should make our life easier.
Let's assume that we're sweeping the lines from the left to the right. Obviously then the code where the intersections will be handled is the code where we process the vertical line. Let's look at this case closer. We can assume that we're going to add some vertical line on with coordinates (x, y1, x, y2), we can also assume that there are some horizontal lines which go through the given x coordinate, we track this set of lines while sweeping left to right. So we're going to add a vertical line and let's say that it has n intersections with horizontal line. Previously we were handling each intersection separately, but you can see that if some horizontal lines already belong to the same set in DSU and they go next to each other then we don't need to handle them one by one anymore. They already belong to the set in DSU so there is no need to join them, we might only need to count the number of them between y1 and y2 coordinates, but that can be calculated in logarithmic time. So the trick to get rid of quadratic time complexity is to avoid storing horizontal lines one by one and store instead an interval (across y coordinate) of horizontal lines which belong to the same set in DSU. I will call these intervals chunks. You will need to manipulate these chunks in logarithmic time and you will need to locate them by y coordinate so you need to store them in a treap or a STL map for example with y coordinate serving as a key.
To be clear let's see what data each of these chunks will hold:
struct chunk{
int top, bottom; // two coordinates which describe the interval covered by the chunk
int id; // id of this chunk in DSU. Several chunks might have the same id here if they belong to the same set in DSU
};
And we agreed that data structure which holds these chunks can manipulate them in logarithmic time.
Let's now get into details to see how exactly it works. While sweeping we will have one of three possible events (listed in the order we need to handle them): new horizontal line starting, vertical line added, horizontal line finishing. First and third operation only update our chunks data structure while the second operation uses it and actually joins the sets. Let's look into each of these operations:
horizontal line start. We need to add one more chunk which will consist of a single point. The only additional operation we might need to do happens when this new line goes through some chunk whose interval already covers this point. In this case we need to split this covering chunk into two parts — top and bottom one. It's a constant number of updates/insertions/removals in our chunk data structure and we agreed that each of these operations can be done in logarithmic time so the time complexity of a single operation of this time is O(logN). It should be also mentioned here that during processing a single operation of this type we might add at most two new blocks. Since in total we have no more than N operations of this type them it means that in total we will have no more than 2·N blocks created. This is important for the further analysis.
vertical line. In this operation we need to find all chunks affected by this vertical line and join them. Each join of two chunks takes logarithmic time and we might have up to n chunks present there, so we might need up O(NlogN) time to draw a single vertical line. This doesn't give us a good estimate. But we can see that we have only two ways to get new chunks — they are either added in the step 1 because it's a new line or one chunk is being split into two when we add a line in between. But we have an upper bound on total number of the chunks in our structure as shown above. Ans since we have such an upper bound then we can say that it doesn't matter how many chunks will join a single vertical line because in total all vertical lines will not join more than 2·N chunks. So we have an amortized time complexity analysis here, in total all vertical line operations will take O(NlogN) time.
There are some other details we need to handle here. For example we need to avoid cycles correctly. This margin is too narrow to contain the proof but the formulae to correct the length sum is like this:
d = y2 - y1 - (Nintersections - 1) + Ndistinctsets - 1
where d — the number you need to add to the sum of the lengths in DSU
Nintersections — number of horizontal lines intersecting with the given vertical line, I used a separate segment tree to get this value in O(logN)
Ndistinctsets — number of distinct sets in DSU joined by this vertical line, you need to count them while joining
So this gives you a way to correct the lengths sums. There is one more thing that needs to be mentioned here — it might happen that your vertical line will be contained by some chunk but will not intersect any horizontal lines in it. In this case you simply ignore this vertical line as if it doesn't overlap any chunk at all.
horizontal line end. Finally we came here and it seems to be simple. When some horizontal line ends we might need to update our chunks. There are three cases here:
a. This line is the only line in the chunks — we simply delete the chunk then.
b. This line lays on some end of the interval covered by the chunk — we update that end. In order to update it we need to know the next present horizontal line or the previous present horizontal line. I used the same segment tree mentioned above to handle these queries.
c. This line lays inside some chunk — we don't need to update that chunk at all.
And that's it! In total it gives O(NlogN) solution.
Author's solution: 7978166 (that chunk data structure is called 'linked_list' in the code because originally I thought it would be a linked list with some way to manipulate it quickly and later I removed all the list functionality).
This editorial was written very late in the night, I'm pretty sure there are tons of typos here, I will proof read it tomorrow, but please don't hesitate to report typos and some minor error to be fixed in private messages.











Appreciative Editorial.................
Thanks for nice contest and editorial :D
Regard to problem C, I think it can be solved in O(1), here is my solution
care to explain this solution?
u can make min
3 - n%3floors. find maximum. letc[i]be number of houses on i-th floor(numeration from 1). letkbe number of floors. notice that(c[1] + c[2] + ... + c[k]) * 3 - k = norc[1] + c[2] + ... + c[k] = (n - k) / 3. min value of sum in the left part isk * (k + 1) / 2. so, whenk * (k + 1) / 2 <= (n - k) / 3u can build k floors. solve it and u'll find maxku can use. ans is(kmax - kmin + 3) / 3There are wrong signs in
c[1] + c[2] + ... + c[k] = (n - k) / 3andk * (k + 1) / 2 <= (n - k) / 3. The '-' should be replaced by '+'.yeah, c is O(1) task 7964152. how hasn't author noticed that?
"Mathematicians would probably solve the quadratic inequation, programmers have two options" pretty much sums up that author indeed noticed a O(1) solution.
sorry, haven't noticed that
With large N,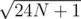 will lose precision, so it's also a good thing that N ≤ 1012 fits the solution in double types. (And consequently for large N, I call that
will lose precision, so it's also a good thing that N ≤ 1012 fits the solution in double types. (And consequently for large N, I call that 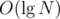 solution too as finding the square root is not trivial; binary searching the square root is reasonable.)
solution too as finding the square root is not trivial; binary searching the square root is reasonable.)
if u use long double, u'll get enough precision
If you are afraid of losing precision you can always check on integers whether your desired sqrt is correct and in case of failure try +-1.
I mean "for large N" means "for N somewhere around 10100 to 10100000", which is beyond the boundaries of the problem. I just say that it's possible to increase the constraints if people can use arbitrary-precision integers.
After a nice announcement now a nice editorial... :)
Never seen a Div2E this complicated before.
In a previous round written by YuukaKazami, no one solved problem div2-E during the contest. However That problem is not much difficult now, because at that time suffix automaton was first introduced to handle string problems, so no one but the author knows it. And later YuukaKazami admitted that it is a fault, because he didn't know div.2 problems C,D,E must be div.1 A,B,C problems, otherwise it will be D.
But a div.2 only round can have such a difficult problem.. This round has set up a new record :p
Thanks for readable solution codes .
why this code get WA? 7967749
Isn't that obvious that if you use hashes you can get WA because of the way the hash works? Hash of one sequence can be equal to hash of another one, but the sequences itself could be different. You just got unlucky here. ;) Consider reading about Anti-hash test and try solving D with Z-function, it's not that hard.
The contest was great :) But I wonder, how have you done that all my hashings algorithms with different keys are failing at 25th test?![submission:7982970][submission:7982847][submission:7968344] How did you create this test?! Thank you!
Hi, 25th test was added based on riadwaw's hack, you can see the generator here, as far as I know it is based on this anti-hash article here, maybe not, you can probably ask him to clarify.
Did anyone else get this problem AC-ed using hash? I did :)
Yeah, that's exactly this test
Lol, E seems so easy now ; d. I'm surprised that nobody came up with this (I was stuck at implementing KMP XD, though either way I didn't have idea after the contest), though it may be not that nice in implementation. There is just this idea with chunks, everything else seems pretty standard ("everyone is clever after hearing solution" :>). Indeed, if it was hard for red coders, it was surely not suitable for Div2, but seeing the results I was expecting really hardcore one :P (my friend even suggested flawed authors' solution xD).
Nice problem and solution, congrats! And +1 for "This margin is too narrow to contain the proof" :>!
Well, the overall idea of these chunks is simple, especially if you would be told to use them then the problem is not that hard, that's true. But coming up with this idea is not so easy, I think especially because you cant't just come up with it, you need to get some idea why it would actually make the entire solution fast enough. And the implementation is not that nice, you're right. Even though you will probably get everything you need to do as soon as you get the idea of chunks, but there are several places you can introduce bugs easily. Both me and Gerald spent some time debugging our solutions and we were in much better situation than participants, cause we had test data and slow reference solution and a lot of time, that situation should have been ringing a bell in my head. Believe me, there is nobody more disappointed in this situation than me, because I gave to Div. 2 a problem which turned out to be good for Div. 1.
What would happen for problem B, If we had P animals instead of only 3? How could we solve it?
The number was chosen especially because you can do that easily with 2 swaps and you don't need to care whether there is some element common for both swaps or not. For example if you ask for 4 permutations it will be different because in the case when you have 3 equal elements you might have to swap first and second, then second and third and then first and second again. That makes it more complicated and less suitable for Div. 2 B. Also in your problem you probably won't be able to ask for large P values, because participant will have to output a lot of numbers and many solutions will time out because of output only, which is not good.
The solution for your problem is still not that complicated though, you will need to break the input into groups of equal elements, let's say that sizes of those groups will be s1, s2, ..., sn. Then the total number of permutations you can achieve is simply s1!·s2!·...·sn!. This gives you an idea whether you can provide P permutations or not. Then you need to provide those, since it grows as factorial of the size of the group then for let's say P < = 1000 it will be enough for you to do permutations within some group of 7 elements because 7! = 5040, so you won't even need to complex things to get next permutation, also in C++ you might find method next_permutation useful for that.
Yeah next_permutation worked for me as marat.snowbear said.
I coded it in the general way as you asked.
Here it goes 7977257
Just need to make few changes in do..while loop
Hope that helps :)
Nice Editorial...****
Thanks for the problem E. It was really nice :)
From Problem C Editorial:
"This means that if you have found some minimum value of floors somehow and you found maximum possible number of floors in the house, then within that interval only every third number will be a part of the solution, the rest of the numbers will give a non-zero remainder in the equation above."
Can anyone explain this more please?
marat.snowbear, can you help me please?
Forget about minimum and maximum, I was just trying to say that from all integer numbers, every third will satisfy the condition that the remainder will be zero. Try it yourself, choose some n and see which numbers x give (n + x)mod3 equal to 0.
Good, I got the idea using the sqrt approach.
For the idea using binary search, where did the formulae that counts the third numbers ans = (Fmax + 3 - 1) / 3 come from?
Hmm, I don't know, I think this is kind of formulae people deduce themselves. This is the formulae which gives you an answer to this question:
In this case the answer would be (n + p - 1) / p.
Well explained editorial, a rarity in codeforces.
an other solution for problem c it gives O(1) cin>>n; a=sqrt(1+24*n)-1; a/=6; if (n%3==1) a+=1; if (n%3==2) a+=2; cout<<a/3;
can you explain it ?!
can anybody help me and tell why my code is showing compilation error. On my system it is working fine. Here is my submission link
you need to include cstdlib on the top of the code.
problem D can be easily solved in nlogn using a good hashing function similar to polynomial string hashing, having the multiplying factor as a prime number over 10^9, say 1000000007, and taking modulo over two distinct prime numbers (also greater than 10^9), so that there is very less chance of collision. here is my solution: 10454545
Please, explain me why (N+F)%3 must be 0! (Problem C)