First I want to thank all the problem solvers!
Hope you had or are going to have a good time with Dreamoon!
If you think there's something that can be improved in this editorial please let me know!
Definitions used in this editorial:
⌈⌉ stands for ceiling function.
⌊⌋ stands for floor function.
 stands for real division.
stands for real division.
For non-negative integer a and positive integer b, div(a, b) stands for integral division, 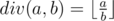 .
.
For non-negative integer a and positive integer b, mod(a, b) stands for module operation, a = div(a, b) * b + mod(a, b).
length(string) is the length of string.
For non-negative integer a ≤ b, A[a..b] stands for the set of A[a], A[a + 1], A[a + 2]... A[b - 1] when A is an array and the substring of A consists of ath to (b - 1)th character(inclusive) of A when A is a string. For such substring we have length(A[a..b]) = b - a.
C(a, b) stands for the combination function, the ways of selecting a elements from a group of b elements.
476A - Dreamoon и ступеньки
We can show that the maximum number of moves possible is n and minimal moves needed is 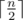 , so the problem equals to determine the minimal integer that is a multiple of m in the range
, so the problem equals to determine the minimal integer that is a multiple of m in the range 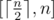 .
.
One way to find the minimal number which is a multiple of m and greater than or equal to a number x is 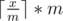 , we can compare this number to the upper bound n to determine if there is a valid solution.
, we can compare this number to the upper bound n to determine if there is a valid solution.
Although best practice is O(1), O(n) enumeration of each possible number of moves would also work.
time complexity: O(1)
sample code: 8212169
explanation of sample code:
The 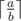 can be calculated in the following c++ code if a is non-negative and b is positive:
can be calculated in the following c++ code if a is non-negative and b is positive: (a+b-1)/b
Because / in c++ is integral division so (a+b-1)/b would result in 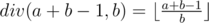
Let a = div(a, b)b + mod(a, b) = db + m, 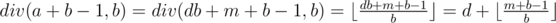 .
.
Which means if 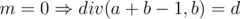 , otherwise div(a + b - 1, b) = d + 1. Can be translated to if
, otherwise div(a + b - 1, b) = d + 1. Can be translated to if 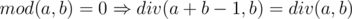 , otherwise div(a + b - 1, b) = div(a, b) + 1. Which matches the value of
, otherwise div(a + b - 1, b) = div(a, b) + 1. Which matches the value of 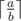 .
.
476B - Dreamoon и WiFi
The order of moves won't change the final position, so we can move all '?'s to the end of the string.
We have the following information:
1. the correct final position
2. the position that Dreamoon will be before all '?'s
3. the number of '?'s
We can infer that the distance and direction dreamoon still needs to move in the '?' part from 1. and 2., and furthur translate that to how many +1s and -1s dreamoon will need to move.
What's left is a combinatorial problem, the probability would be 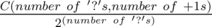 .
.
So we can compute that formula within O(n) time assuming n is the length of commands, but since N is small so we can brute force every possible choice of '?' with some recursive or dfs like search in O(2n) time complexity.
Note that the problem asks for a precision of 10 - 9, so one should output to 11 decimal places or more.
time complexity: O(n), assuming n is the length of commands.
sample code: 8215177
476C - Dreamoon и суммы / 477A - Dreamoon и суммы
If we fix the value of k, and let d = div(x, b), m = mod(x, b), we have :
d = mk
x = db + m
So we have x = mkb + m = (kb + 1) * m.
And we know m would be in range [1, b - 1] because it's a remainder and x is positive, so the sum of x of that fixed k would be 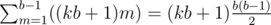 .
.
Next we should notice that if an integer x is nice it can only be nice for a single particular k because a given x uniquely defines div(x, b) and mod(x, b).
Thus the final answer would be sum up for all individual k: 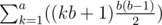 which can be calculated in O(a) and will pass the time limit of 1.5 seconds.
which can be calculated in O(a) and will pass the time limit of 1.5 seconds.
Also the formula above can be expanded to 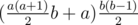 . Dreamoon says he's too lazy to do this part, so if you use O(1) solution you just computed the answer faster than Dreamoon!!!
. Dreamoon says he's too lazy to do this part, so if you use O(1) solution you just computed the answer faster than Dreamoon!!!
Note that no matter which approach one should be very careful of overflowing of the integer data type of the used language. For example one should do a module after every multiplication if using 64-bit integer type. And pay attention to precedence of operations: take c++ for example a+b%c would be executed as a+(b%c) instead of (a+b)%c, another c++ example a*(b*c)%m would be executed as (a*(b*c))%m instead of a*((b*c)%m).
Thanks saurabhsuniljain for pointing out the preceding problem and examples in the comment!
time complexity: O(1)
sample code: 8215188
476D - Dreamoon и множества / 477B - Dreamoon и множества
The first observation is that if we divide each number in a set by k, than the set would be rank 1. So we could find n sets of rank 1 then multiple every number by k.
For how to find n sets of rank 1, we can use {6a + 1, 6a + 2, 6a + 3, 6a + 5} as a valid rank 1 set and take a = 0 to n - 1 to form n sets and thus m = (6n - 1) * k.
The proof that m is minimal can be shown by the fact that we take three consecutive odd numbers in each set. If we take less odd numbers there will be more than 1 even number in a set which their gcd is obviously a multiple of 2. And if we take more odd numbers m would be larger.
The output method is straight forward. Overall time complexity is O(n).
time complexity: O(n)
sample code: 8215198
476E - Dreamoon и строки / 477C - Dreamoon и строки
First let A[i] to be the minimal length L needed so that substring s[i..i + L] can become pattern p by removing some characters. We can calculate this greedily by keep selecting next occurrence of characters in p in O(length(s)) time for a fixed i, so for all i requires O(length(s)2).
Next we can do a dp D[i][j] where D[i] is the answer array for s[0..i]. D[i] can contribute to D[i + 1] with 0 or 1 removal and to D[i + A[i]] with A[i] - length(p) removal(s). In other words, D[i][j] can transition into tree relations D[i + 1][j] = D[i][j] //not delete s[i], D[i + 1][j + 1] = D[i][j] //delete s[i], and D[i + A[i]][j + A[i] - length(p)] = D[i][j] + 1 //form a substring p by deleting A[i] - length(p) characters. Calculate forwardly from D[0] to D[length(s) - 1] gives the final answer array as D[length(s)]. Calculating D[i] requires O(length(s)) time for a fixed i, so for all i takes O(length(s)2) time.
time complexity: O(n2), n = length(s)
sample code: 8215203
Another solution:
Let k = div(length(s), length(p)). We can run an edit distance like algorithm as following (omitting the details of initialization and boundary conditions):
for(i=0;i<n;i++)
for(j=0;j<k*p;j++)
if(s[i]==p[j%length(p)])
D[i][j] = D[i-1][j-1]
D[i][j] = min(D[i][j], D[i-1][j] + (j%length(p)!=length(p)-1))
That means remove cost is 1 when it is in the middle of a p and 0 elsewhere because p need to be consecutive(thus no need to be actually remove outside of a p). Then D[n][t * length(p)] is the minimal number of removals to have t non-overlapping substring of p. So we have answer[D[n][t * length(p)..(t + 1) * length(p)] = t. And after the maximal t is reached, decrease answer by 1 for every length(p).
time complexity: O(n2)
sample code: 8215394
477D - Dreamoon и двоичное исчисление
Let Xb be the binary string of number X. An ideal sequence can be expressed as a partition of Xb: P1 = Xb[1..p1], P2 = Xb[p1..p2], ... PK = Xb[pK - 1..length(Xb)] where Pi ≤ Pi + 1. The length of operations of such sequence is PK + K.
We can calculate the number of different ideal sequences by dp. State D[i][j] stands for the answer of state that we have print Xb[1..j] and last partition is Xb[i..j]. A possible way of transition is that a state D[i][j] can go to state D[i][j + 1] and D[j][k] where k is the minimal possible position such that value of Xb[j..k] is equal to or greater than the value of Xb[i..j] and Xb[j] is 1 since we can't print any leading 0.
Note that D[j][k + 1] can also derived from D[i][j] but it will covered by D[i][j] → D[j][k] → D[j][k + 1], so we don't need to consider this case to avoid redundant counts.
If we can determine k for each i, j pair in O(1) then we can compute this dp in O(length(Xb)2) in the following manner:
for(j=0;j<n;j++)
for(i=0;i<j;i++)
compute the transitions of D[i][j]
So let's look into how to calculate the value k for a given i, j pair. If the value of Xb[j..2j - i] is equal to or greater than Xb[i..j] than k is 2j - i because if k is less than 2j - i would make length of the new partition less than the previous partition thus its value would be lesser. And if k can't be 2j - i, the value of 2j - i + 1 is always a valid choice because it would make the length of the new partition greater than the previous one. So for each length L if we know the order of Xb[i..i + L] and Xb[i + L..i + 2L] in O(1) time we can calculate k in O(1) time(can be easily shown by assuming L = j - i).
One way of doing such is using prefix doubling algorithm for suffix array construction to build a RMQ structure for query in O(1) time. The prefix doubling algorithm requires O(nlgn) precompute time. Note there is still a various of ways to do this part of task in the same or better time complexties.
And for the shortest length part we can compute the minimal parts needed so far for each state along with the preivous dp. Then compare all states ends with j = length(Xb).
Overall we can solve this problem in O(length(Xb)2) with caution in details like boundaries and module operations.
time complexity: O(n2), n = length(Xb)
Note the sample code use a nlgnlgn version of prefix doubling algorithm
sample code: 8215216
477E - Dreamoon и блокнот
Although swapping two parts of a query would result in different answer, if we reverse the lines length alltogether then the answer would stay the same. So we only analyze queries where r2 ≥ r1.
The answers would comes in several types, we’ll discuss them one by one:
1. HOME key being pressed once: the answer will be 1(HOME) + r2 - r1(down keys) + c2(right keys). Note that this is the best answer if the HOME key is ever pressed once, so we won’t consider HOME key anymore. This step is O(1) for a single query, thus O(q) in total.
2. direct presses r2 - r1 down keys and no or one END key in those rows: because the cursor position will be reset to the row length if we go down to a row with length less than current cursor position, the possible positions that can be at row p if we start at end of each previous rows can be track with a stack. The position directly pressing only down keys from r1 to r2 is min(c1, the length of first row after r1 in stack). We can use a binary search to get the first row after or equal r1 in stack. From that row till r2 in the stack are the positions possible when pressing ONE END key (pressing more won’t get more possible positions), we can use a binary search to find the position closest to c2 which is the best. We can sort all queries and use O(qlgn) time for queries and O(n) time for maintaining stack, so O(qlgn + n) in total.
3. go back some rows and press one or no END key at the row: we only interested in END OF rows in stack constructed in 2.. We can use a binary search in stack to identify the range of rows interested. For those lengths of row less than c2(also can use a binary search to locate) we only need to consider the first one encountered(closest to r1), note still need to consider if it needs an END key for this case. For those lengths of row greater than or equal to c2, the answer would be r1 + r2 - 2 * (row reached) + (length of the row) - c2 + (1 if length of the row greater than c1). The terms related to row in the previous formula is 2 * (row reached) + (length of the row) + (1 if length of the row greater than c1). We can identify the range with and without +1(last term) and query in a segment tree of the minimal value of 2 * (row reached) + (length of the row) for each range. Thus the time need here is O(nlgn) for maintaining segment tree and O(qlgn) for query while sharing with the stack of 2., so O(nlgn + qlgn) in total.
4. go beyond r2 some rows and press no or one END at the row: this needs a reversed stack and very similar approach of 3.. The time complexity is the same as 2. and 3..
So the total time complexity is O((n + q)lgn), note this problem is very hard to get the code right.
time complexity: O((n + q)lgn)
sample code: 8212528










Div 2 A & B that;s it. Please don;t mind but i don;t think this is the expected editorial ! :P
Sorry for slow update, I'm still working on the rest of the problems.
No no please don;t be.I was just saying had the editorial been fully updated then it would have been better but definiately that;s not a issue !
Please don't use ; in place of '
Some solutions for Div 2 C failed system test, because of % precedence. Can you provide more detail on this??
wrote more into that part :)
drazil No not only precedance with +, but with * also, here is a code which failed system test.
Thanks! Added that example, too!
Nice solution for Div 2 D. :)
I got nice "if" in B (http://codeforces.com/contest/477/submission/8186812)
:)). I've thought that it was needed :D. What hasty people can create :D.
Hey drazil when I click on your solution to 476E/477C (this link), CF yields I'm not allowed to view it. Please check this. Thanks!
Sorry for that, is just this particular code or all the code posted in the editorial? In fact I have no clue of how to make the code public, still trying.
Hey there. No worries. I clicked on 476A's and it worked. One thing you could try is to submit in practice mode (here, which would give you a public link. Then you could update the editorial.
now all links should be accessible
For Div1-C,
D[i] can contribute to D[i + 1] with 0 or 1 removal and to D[A[i]] with A[i] - m removal(s)is not clear. Can you please write some more details?After required number of deletions, you'll have a final string. To obtain this from the old string, we'll do the processing as follows, for each position you have 3 options, either skip it and allow it in the final string, or delete it and hence it won't appear in the final string or start a required pattern with that character if possible.
Case 1 contributes for 0 removals and contributes to idx+1.
Case 2 contributes for 1 removals and contributes to idx+1.
Case 3 contributes for A[i] — m removals and contributes to index = A[i].
See my code for clarity :)
Sorry there is some bug in the original paragraph, now should be fixed and added more explanations.
dp and math problems all the way! Awesome problemset :-D.
+1 for an well-written editorial and thanks for the contest.
It's an arguable question — should/shouldn't we expect some level of implementation difficulty from problem div1 B. But it's not a secret that it shouldn't be easier than div1 A. "Let's note ... and find the result in O(1)" — It's not a level of div1 B, even if you're added output with O(n) complexity.
PS but now I know that div1 B may have solution with 3-4 lines, I've never seen this before)
This is a problem whose solution has only one line. (That is a really hacky way to force one-liner though; seriously,
input() * 0to skip one line from input?)By the way, during that round, Problem A is harder than Problem B.
So many math problems... Makes me really worried about my math skills.
this is good for theory!!:)
You can get PhD degree in "Cheating theory of Codeforces contests".
cheat I don't cheating but i send message but I don't cheating I solve problem by yourself !:)
I love how he says "I solve problem by yourself"..
Well obvious cheating :) But I'm wondering how did you get the image...
Must from here.
In the third question it should be m can take values (0,b-1].
You're right! Since x is positive, m ≠ 0.
I guess my solution of B problem is a bit simpler. At least I didn't use math :D Well, since the length of input strings is only <= 10, it turns out you could recursively brutforce all possible positions, which guy_2 can lead to, and then divide the number of possible positions equal to the correct position, which guy_1 led to, by 2 ^ (number of '?' in second string).
During the contest I misread the limit for n (lenght of the string) in problem Div1-C, I thought it was n ≤ 10000. -sized table :)
-sized table :)
However I wrote a quadratic solution similar to the first one explained in the editorial. Obviously I got a memory limit error, because a table of 108 integers is too large...
In a hurry I edited the algorithm, and managed to solve the problem using a
Could somebody explain the O(1) solution of DIV2-A? Specifically this
int ans = (lower_bound+m-1)/m*m;part looks like voodoo magic to me.I mean I get the gist that
(lower_bound+m-1)/mresults in 1 or 2 (?) because it's casted to int and then*mshows the number of moves, but why does it work this way?Added some explanation of this sample code up there =)
My apology, I did not get the explanation either. Can someone please help?
We are trying to find ⌈ x / m⌉ * m where x = ⌈ n / 2⌉
In the sample code, lower_bound is the x.
In the sample code, we use the fact that ⌊ (x + m - 1) / m⌋ = ⌈ x / m⌉ and the nature that the division in c / c++ language is performing the floor function if the resulting value is a floating point.
So ⌈ x / m⌉ * m = ⌊ (x + m - 1) / m⌋ * m, and in c / c++, we can write (x+m-1)/m*m to get this value.
Sorry for the late response. If this answers your question, please let me know and I'll update the editorial.
Regarding 272D: where the hint about relatively prime numbers comes from {6a + 1, 6a + 2, 6a + 3, 6a + 5}? Is it an observation which the participant is assumed to see?
I've written it before. Basically, you need three odd numbers in a set, and the rest is a little guess and be lucky.
Drazil in div2 C a,b<=10^7 and i used int. But it gives me error. But when i used long long it passed. Why?
There is an overflow in
m*(m-1)part oflong long t=m*(m-1)/2;withint m;sincem*(m-1)/2will be calculated first(with int) and the result(which overflowed) will then be cast to long long.476D — Dreamoon and Sets / 477B — Dreamoon and Sets Why the set is {6a + 1, 6a + 2, 6a + 3, 6a + 5}
It's a valid and optimal(in terms of m) one(this should not be hard to verify). There's still many other possible solutions, just stick to 3 odd numbers and 1 even number in each set while they're co-primes to make it optimal(in terms of m, again).
Thanks.
In my solution of div1 D, I didn't use the prefix doubling algorithm, but instead got the suffix array by throwing all suffixes into a trie and (independently) computed the LCPs of all pairs of suffixes in O(N2) time. The memlimit is kinda tight in this case, but sufficient with proper vertices of the trie).
vertices of the trie).
reserves (onDeciding if 2 consecutive substrings of equal length can be created in successive operation 1-s is then just a question of checking if they have the right order in the suffix array or a sufficiently long LCP.
Hashing with binary search should work too. Though that would make it O(N^2 * log n), but it shouldn't pose any problem since n <= 5000.
I've solved it the same way, but by calculating Z-function for every suffix of s.
UPD: Sorry, didn't notice ifsmirnov entry.
For D you can also use Z-function to compute LCP(i, j). Just compute z(s[i..n]) for all suffixes of S.
BTW, there is a bug in your code for D:
j < j.hee.....
fixed, thanks!! I have no idea why I typed j < j.
In Div 2 B editorial, can someone explain me combinatorial part? Why do C(no. of '?'s, no. of +1s) give us the number of ways to get desired distance?
From the input we can figure out number of '+' we need and number of '-' we need to end up at the correct location. Out of all the question marks, we need to replace (number of +) of them with '+', and the rest of the question marks we will replace with '-'. C(no. of '?', number of '+') is the number of ways for us to choose the (number of '+') locations out of the (no. of '?') locations to replace with '+'. Does that make sense?
I am unable to get how (distance + moves)/2 = no of +. Any Help?
For Div1C, I used the DP[m][j] which stores the minimum number of characters to be removed from s[j], ..., s[s.length-1] so that we can achieve m pattern (p). In here, I precalculated A as you described, so that DP[m][j]= Min( ( DP[m-1][A[j]+1] + (A[j]+1-j)), (DP[m][j+1]) ). This is because you can choose a pattern that starts at index j if the first letter matches. Otherwise, DP[m][j]= DP[m][j+1]
In problem B, i used the same logic as given in the editorial but forgot to write the condition that if (distance+moves)%2!=0 then print zero {refer to this code to know values of distance and moves} and still got AC. Is this due to weak test cases or am i missing something? My solution without the condition: 27922830
Great observation!
Actually, it can be proven that (distance + moves) % 2 will always equal to 0!
in the editorial for problem div2E/div1C, what is j in state dp[i][j] or what does dp[i][j] denote ? please help.
The j is the number of characters removed, which corresponds to the x in the ans(x) in the problem statement.
Hope that answers your question. Please let me know if so, I'll put it in the editorial.
For div2C how do you get x = db + m?
If anyone requires further explanation for problem Div2 D — Dreamoon and Sets, I have written an extensive blog post here I explain both how to come up with the set and how to prove it.
What happend in test #26 of Div1C? Seems that most contestants FSTed on this test, and I am now also stuck at it.
The first solution to div2 E / div1 C given in the editorial considers dp in the form of transitions. There's a much easier formulation in terms of recurrences that can be coded as a top down dp. You may refer to my code for details: 51684294. I have commented it for better understanding.
The solution for Problem A seems magical to me so I am sharing my approach:
Let us take 1 jumps 'a' number of times and 2 jumps 'b' number of times. Therefore, a + 2*b = n Also, a + b = k*m, where k >= 0, is any positive integer constant
Now, substracting 2 from 1, b = n — k*m => k*m = n-b => k = (n-b)/m
To get a positive Integer k, (n-b) must be divisible by m Therefore our task is to find a value of b, for which (n-b) is exactly divisible by m Now, where to start iterating from? We know, a + 2*b = n Therefore, the maximum value of b can be n/2, if we take a as 0. Also, we need to ** minimize** the total jumps, hence, we take more jumps of 2 and less jumps of 1. Therefore, we try to increase b as much as possible. This is why, let's start with b as n/2 and slowly keep decreasing it till it becomes 0. There is no need to go below 0, because a*1 + 2*0 = n will be satisfied for a = n, always.
This is my code:
Sorry for my poor grammar.