499A - Watching a movie
One can solve the problem using greedy algorithm: if we can skip x minutes at current moment without skipping any good moment — we do that, otherwise — watch another minute of the film.
499B - Lecture
In this task you must find for every string in the text the pair containing that string, and from two strings of that pair output the shortest one.
498A - Crazy Town / 499C - Crazy Town
It can be easily proved that, if two points from statement are placed on different sides of some line, this line will be crossed anyway. So, all we need to do is to cross all these lines, so the answer is the number of these lines.
To check if two points lies on different sides of a line one can simply use its coordinates to place in line equation and check if these two values have different signs.
Solution complexity — O(n).
498B - Name That Tune / 499D - Name That Tune
Let's numerate all the songs and seconds starting from 0.
Problem will be solved using DP approach. State will be described by two integers (i, j): dp[i][j] is probability of that we named exactly i songs, and the last named song was named exactly before j'th second (after j - 1 seconds). dp[0][0] = 1 obviously.
To make a move from state (i, j) to state (i + 1, j + k) (1 ≤ k < ti), we must name the song exactly after k seconds its playing — probability of that is (1 - pi)k - 1·pi.
To fixed state (i + 1, j) sum of that moves can be represented as  . Simple calculation of this value for each state gives O(nT2) complexity, so one must notice, that this values can be calculated using two pointers for fixed i (in common case it represent a segment with ti length) for every j in time O(T). This way calculating this type of moves takes O(nT) time.
. Simple calculation of this value for each state gives O(nT2) complexity, so one must notice, that this values can be calculated using two pointers for fixed i (in common case it represent a segment with ti length) for every j in time O(T). This way calculating this type of moves takes O(nT) time.
There is also a move to (i + 1, j + ti) and a move from (i, j) to (i, (j + k) = T), when we couldn't name current song in time T. This types of moves is calculated with O(nT) too.
Solution complexity — O(nT).
498C - Array and Operations / 499E - Array and Operations
We will divide only by prime numbers.
First, let's build a graph, where each of n numbers have own vertex group:
Find all prime factors of current number. Every factor will have its own vertex in a group, furthermore, if some factor p has power of ai in current number, it will have exactly ai vertexes in group.
The number of vertexes in such graph is 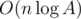 .
.
Now we will make edges in our graph: edge between two vertexes exists if and only if there is a good pair (given in statement) of vertexes group numbers and the prime values of a vertexes are the same. That means that we can divide that group numbers by that prime.
The number of edges is 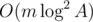 .
.
Good pairs are given the way that our graph is bipartite. After finding maximum matching in this graph we represent the way of doing operations as described in the statement.
As soon as solution is using Kuhn's algorithm, its complexity is 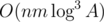 . One could notice that some of the edges are useless and reduce it to
. One could notice that some of the edges are useless and reduce it to 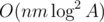 .
.
498D - Traffic Jams in the Land
The solution of a problem — 60 (LCM of a numbers from 2 to 6) segment trees.
In v'th segment tree we will hold for every segment [l, r] the next value: minimum time needed to get from l to r if we start in a moment of time equal to v modulo 60. Using these trees' values it is easy to quickly answer the questions, carefully changing the trees' values.
498E - Stairs and Lines
The problem is solved using DP approach dp[i][mask] — the number of ways to paint first i blocks of a ladder the way that the last layer of vertical edges is painted as described in mask mask. This could be easily recalculated using matrix M[mask1][mask2] — the number of ways to paint horizontal edges between two neighbour vertical layers painted as represented by masks mask1 and mask2.
For fixed i we have wi layers, so this matrix must be multiplied by itself wi times, which can be quickly done by binary-pow algorithm. After that this matrix is simply used in dynamic described above.
Solution complexity — 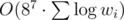 .
.











So fast !
In problem B one could simply code an O(NT2) solution and make a 'break' every time when the current probability is small enough (I used 1e-15 as threshold).
I used hashtable to solve it ,i didnt get TLE. You can view my code here Is it effient way to do ? My solution
He's talking about Div1 B / Div2 D and your solution is for Div2 B.
For B, I believe that many contestants coded an O(nT) solution, but still got TLE regardless, including myself. Maybe the time limit of 1s was slightly too short?
Here is my code below: is there anything I could have done to speed it up enough? http://codeforces.com/contest/498/submission/9255020
Copying array requires much time.
Swapping pointers is better.
dp1[j] += dp[j-ti[i]]*powers*(1-pb[i]); what if j — ti[i] < 0 ? I am not sure, is because of that, but it is undefined behavior.
Above I have
if (j <= ti[i]) { dp1[j] = dp1[j-1]*(1-pb[i]) + dp[j-1]*pb[i]; continue; }
This takes care of the undefined behavior.
oh, sorry for that, I didn't notice ^-^
for myself: never use standard pow, I failed B, because of that.
Well, in my code I use std::pow n < = 5000 times, and store it as the double powers. So this cannot be why my code TLE, right?
I used std::pow O(n2) times and got OK.
I got TLE because I stored them in an array :(
TLE: 9259374
AC: 9259494
Спасибо вам, за качественные задачи и за быстрый разбор.
In Div1 B/Div2 D, I'm having trouble to find the mistake in my solution :( I get WA on pretest 6 9257394
I basically do
where t is the time, n is the nth song and curplay is the time the current song has been playing.
Can anybody help ?
please :)
Finally became an expert.. yipee :)
It is 5 years since your last and first becoming an Expert-ranker :( Good luck mate, you are almost Expert again
in Div 1 C , why does not my strategy work correct . Plz help dans http://codeforces.com/contest/499/submission/9262810
Greedy does not work for this problem. Try this test:
4 3
8 12 8 12
2 3
1 2
3 4
Merry Christmas to everyone !! Became expert !!
put me minus !!!
Ok ;). Merry Christmas :)
why this solution does not work for problem C Div 2
9264650
Try to avoid double comparison because it causes errors. If you have to, use epsilon which is a very small value like that: Instead of saying that (double1 == double2) say (fabs(double1-double2)<=1e-7)
I'm not sure that is the mistake. However in this problem you don't need to use doubles so why do you use them ?
why dont you attach the code with every problem??? Its really helpful. Please do it. Looking at the solution is difficult for someone trying to understand the solutions of harder problems. Frustrated. :(
EDIT: I discovered the problem and solved it, but anyway that is O(nT^2) so it gets TLE. The idea is correct but in the code I had a mistake in the first condition and I fixed it.
In problem Name That Tune I can't understand the third paragraph. Can anyone explain it more clearly?
Besides, I want to know why my idea is wrong. According to my idea, DP(i,j) = The expected value of number of recognized songs if I started from song i and j seconds have passed. So DP(i,j) =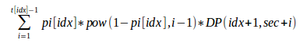 + pow(1 — pi[idx], ti[idx] — 1) * DP(idx + 1, sec + ti[idx]) . And the answer is DP(0,0)
+ pow(1 — pi[idx], ti[idx] — 1) * DP(idx + 1, sec + ti[idx]) . And the answer is DP(0,0)
Hope someone tells me what's wrong with the idea or the code. Here is the code:
I have the same doubt. danilka.pro please explain the mistake.
What is the exact complexity of Kuhn's Algorithm? Is it O(N*E)? Also, O(n*m*logA^3) = 100*100*30*30*30. Yet it passes the time limit. Probably cause of the heuristics inside the algorithm. How can we know for sure that Kuhn's algorithm with heuristics will be able to pass the time limit?
That's a very good question. Sorry, I'd forgotten to translate my remark about reducing complexity to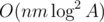 . Now it's done.
. Now it's done.
The number of vertices is $$$O(NlogA)$$$ and the number of edges is $$$O(Mlog^2A)$$$. Therefore if we use Edmond Karp for this, the time complexity should be $$$O(NM^2log^5A)$$$. This should not pass the TL, right? Here is my solution that passes https://codeforces.com/contest/498/submission/104527559 in 140 ms
To find the number of lines (in the input) which passes the line (x1,y1,x2,y2) you could also use this way: Consider the name of the line (x1,y1,x2,y2) d Find the intersection of each line in the input with d. (By solving 2 equations). If the intersection (answer of equation) is between our 2 points, then the line crosses d. So we should +1 our answer. It has a little bug: When the gradient becomes infinity which should be solved with an if.
This is my code: Submission Link
problem D(Div.1) can be solved also by sqrt-decomposition. For each city i and for each time v (modulo 60) you should store the total time which is needed to get from city i to the last city which is in the same bucket.
My submission: 9259900
Please Someone explain Div1 B elaborately. Specially transactions between the states ..
Thanks in advance :)
In problem Div 1 B (Name that tune), I could not understand approach to reduce the complexity from O(N*T^2) to O(N*T). Any detailed explanation is really appreciated.
Thanks
Neither can I. If anyone help us to understand that would be a great hand :)
well suppose you have dp[i-1][0..T] and you want to calculate dp[i][0..T]
naive approach: dp[i][7] = dp[i-1][6] * (1-p)^0 * p + dp[i-1][5] * (1-p)^1 * p + dp[i-1][4] * (1-p)^2 * p..
notice that dp[i][8] = dp[i-1][7] * p + dp[i-1][6] * (1-p)^1 * p + dp[i-1][4] * (1-p)^2 * p +...
it's just dp[i][7] * (1-p) and adding the top element (dp[i-1][7]) and possibly removing last element (because of Ti)
Once we have calculated the entire dp[0...n][0...T] array , how do we find out the answer?
As we know that the game lasts T seconds, we are interested only in dp[i][T] values (possibility of that exactly T seconds passed and exactly i songs named), so the answer is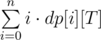
danilka.pro, is this dp[][] the same as in the editorial? If it is, can you obtain the answer this way? (next part is to people like me that didn't get the answer to the problem even reading the editorial) In the dp[][] from editorial you can sum all dp[i][j] to obtain the answer. The motive is that the expected value of the number of music discovered till T is the sum of expected value E(i, j) of the random variable that is 1 if one change to music i in second j. This is true because if we have Q songs discovered till T, then we had Q changes till second T. (i think my explanation is a bad one).
Thanks.
Or if we define dp[i][j] as the probability of guessing i songs in j seconds s.t. that the last song (the i-th one) was guessed exactly at the j-th second, then the answer is
Can you explain in more details?
Here's how to reach the formula:
Let $$$dp[i][j]$$$ be the probability that $$$i$$$ songs are recognized in $$$j$$$ seconds and the last ($$$i$$$-th song) was recognized exactly at the $$$j$$$-th second and $$$P_i$$$ be the probability that the $$$i$$$-th song is recognized.
Let $$$X$$$ be the random variable for the total no. of songs recognized. Also, let $$$X_i$$$ be the indicator random variable denoting whether $$$i$$$-th song is recognized $$$(X_i = 1)$$$ or not $$$(X_i = 0)$$$.
So, $$$X$$$ can be written as: $$$\sum_{i = 1}^{n} X_i$$$.
Now, $$$E(X) = E(\sum_{i = 1}^{n} X_i) = \sum_{i = 1}^{n} E(X_i)$$$. [By linearity of expectation]
and $$$E(X_i) = P_i = \sum_{j = 1}^{T}dp[i][j]$$$
So, the final answer becomes $$$\sum_{i = 1}^{n} \sum_{j = 1}^{T} dp[i][j]$$$.
Note here that the $$$X_i$$$'s are not independent. Since if $$$X_i = 0$$$, then $$$X_{i+1} = 0$$$, but we exploit the fact that linearity of expectation can be applied regardless of whether the variables are independent or not.
Rest is implementation and optimization which is very tricky for this particular problem and you'll probably have to look at other people's submissions to try to understand that or get more comfortable with solving problems like these and then come back later to solve this problem once you have enough experience since it involves a lot of tricky formulas and implementation.
Thanks Nezzar. Its very much clear now.
Funny fact: problem A from div1 was already used for a CF round very long time ago, and it was problem D for that contest (well, now we have lines instead of circles...) :)
Why does a greedy algorithm not work in 498C? By greedy I mean take a good pair x, y and divide the two number a[x] and a[y] by as many prime factors as possible. Shouldn't it give the same result?
Nevermind, I got my mistake. But I don't understand what the author means by this vertex group in the graph and how does the graph become bipartite. Someone please explain!
graph becomes bipartite because u only have pairs a[i], a[j] such that i + j is odd. it means that if i is odd then j is even. Or if i is even then j is odd. so you have numbers with odd indices on one side, numbers with even indices on second.
As the problem says good pair will always be odd number, so there is an even and a odd number in each good pair. So u can arrange all good pair such that odd will be in one side and even will be in other side. Thus it can be bipartite. And if u factorize one number, then all prime number will be in one vertex group.
What is a vertex group? A group of vertices in a graph? How does that work?
For example, if you have a number 12 -> so to represent it, we use two vertexes (2 , 3) because 12 = 2^2*3, and then, connect only matched prime in match pair, so you have your graph.
what's the problem with the greedy approach. can you explain ?
Consider the case
4 3
2 2 2 2
1 2
1 3
2 4
Here greedy will give 1: taking a factor of 2 from 1,2. The answer is 2: taking factors of 2 from 1,3, and 2,4.
Could anyone please, explain me the third test of the Name That Tune:
I am thinking this way: p(0;0)=1 p(1;1)=p(0;0)*0.5=0.5 p(1;2)=p(0;0)*(1-0.5)*0.5=0.25 p(1;3)=p(0;0)*(1-0.5)^2*1=0.25 p(2;2)=p(1;1)*0.5=0.25 p(2;3)=p(1;1)*(1-0.5)*1+p(1;2)*0.5=0.375 p(3;3)=p(2;2)*0.25=0.0625
M=p(1;3)*1+p(2;3)*2+p(3;3)*3=1.1875
Where have I missed 0.5?
Thank you
I found answer of that case is, 1.187500000 too.
What is wrong in my code?:
include <bits/stdc++.h>
using namespace std;
long long n, x, l[10010], r[10010], ans, res;
int main(){ cin >> n >> x; for(int i = 1; i <= n; i ++){ cin >> l[i] >> r[i]; } ans ++; int j = 1; while(j <= n){ if(ans + x < l[j]){ ans += x; } else { res += r[j] — ans + 1; j ++; } cout << ans << ' '; } cout << res; return 0; }
This is not the proper way to give your code. First submit it, then share the link.
Code Where is my mistake?
Click it
ty
Try this one
For problem C div 1, the test is weak, I just use bipartite graph without factorized those numbers, but it still passed the system test. My submission
Div1A — "It can be easily proved that, if two points from statement are placed on different sides of some line, this line will be crossed anyway. So, all we need to do is to cross all these lines, so the answer is the number of these lines." — that is completely obvious why we need to cross all lines such that home and university are on its opposite side, but what is very important — why it suffices to cross them just one time, why there exists a route such that we do not need crossing it more than one time?
I know answer to that question, but I just wanted to point out that saying "it can be easily proven that something obvious" and not mentioning something significantly harder is pretty funny.
What is the expected complexity to Div1D? I coded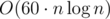 and optimized it pretty much everywhere where I could and it passed, but TL was 2s and my time was 1,93s...
and optimized it pretty much everywhere where I could and it passed, but TL was 2s and my time was 1,93s...
By the way TL's were very strict in that contest. Amount of people which got TLE on B and E is too damn high. TL to D was also strict, but maybe maxtest was included in pretests, so it didn't cause that many TLE on systests. I always emphasize that there is no point in setting constraints to be as high as possible. It's always very sad to fail, because of some random TLE on systests and it was very often case in that contest.
I know it's 3rd post in a row, but since they all regard to different issues I think it's better to keep them apart.
I could be mad.... I have got TLE4times.... who can give me some help for div2 D here is my code 10266510
I have been getting time limit exceeded on test 65 for 498B (Name that tune). I would be glad if someone could quickly glance at my code and tell me how I am exceeding a runtime of O(nT). This is the link to my code: http://codeforces.com/contest/498/submission/12256295
I'm getting the same problem. don't worry the constraints are unnecessarily tight. My solution was also O(n*T).
An easier way to solve div1 C / div2 E: Try to maximize the no. of operations for every prime factor that occurs in any of the numbers by constructing a flow network that corresponds to a bipartite graph with even indexed vertices in the first partition and odd indexed vertices in the second partition (assuming 0 based indexing). An edge from the source to a vertex i with weight j for the graph corresponding to a prime no. p means that i lies in the first partition and p occurs as the jth power in the ith number. Similarly if i would have been odd indexed, we would have had an edge from i to the sink of weight j. The remaining edges are the edges between the partitions that correspond to good pairs having infinite (or 100) capacity (Since flows from source to the vertices in the first partition and from vertices in the second partition to the sink already put a restriction that the no. p cannot be taken more times than it occurs in the ith no.) . Here is an implementation by rng_58. I understood the solution to the problem from this submission itself.
This makes it easier to think in terms of flow, thanks. Got AC with this approach.
I have a doubt though, I used Edmonds Karp algo which has a running time of O(nm^2). Now for each prime in set X, I am running the same algorithm, where X is the set of prime numbers that are prime divisor of all the input numbers. Now how can we deduce the limit on size of X. I mean O(nm^2) is already around 4e6, and to fit in the 1-second limit (or around 1e8 operations), how would I have originally got the limit on size of X to be less than 25.
{deleted}
For the make the tune question, I've done 13 wrong submissions. I'm still getting tle. My solution is O(n*T) but keeps failing on testcase 65. The setter mustn't have kept the constraits for that problem so tight knowing that people will use long double for storing the elements. I even removed that and made a lot of changes to optimize my code but it's still getting tle. It works fine when I run a random testcase 5000*5000 in my machine.