507A - Amr and Music
Problem: We have to split the number k into maximum number of elements of ai such that their sum is less than or equal to k.
Hint: To maximize the answer we have to split the number into the smallest numbers possible.
Solution: So and since the limits are small we can pick up the smallest element of the array and subtract it from k, and we keep doing this n times or until the smallest number is larger than k. Another solution is to sort the array in non-decreasing order and go on the same way.
Time complexity: 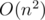 or
or 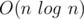
Implementation: 9529124 .
507B - Amr and Pins
Problem: We have a circle with radius R at position (x, y) and we want to move it to (x', y') with minimum moves possible. A move is to choose an arbitrary point on the border of the circle and rotate the circle around it with arbitrary angle.
Hint: What is the shortest path between two points? A direct line. So moving the center on that line with maximum move possible each time will guarantee minimal number of moves.
Solution: Let's draw a straight line between the two centers.
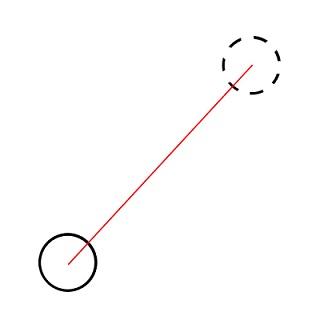
Clearly to move the center with maximum distance we need to rotate it around the intersection of the line and the circle with 180 degrees. So the maximum distance we can move the center each time is 2 * R. Let's continue moving the center with 2 * R distance each time until the two circles intersects. Now obviously we can make the center moves into its final position by rotating it around one of the intersection points of the two circles until it reaches the final destination.
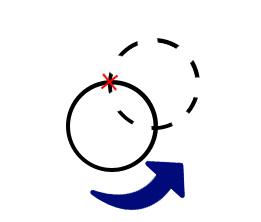
Every time we make the circle moves 2 * R times except the last move it'll be ≤ 2 * R. Assume that the initial distance between the two points is d So the solution to the problem will be 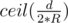 .
.
Time complexity: 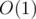
You have to be careful of precision errors. Here is a code that used only integer arithmetic operations 9529147.
507C - Guess Your Way Out!
Hint: Simulate the algorithm until we reach a leaf node assume that it's not the exit. Now the question is Are there some nodes that are guaranteed to be visited before trying to reach the exit again?
Solution: The first observation is that in order to return to a parent we will have to visit all nodes of the right or the left subtree of some node first. Now imagine we are in the situation below where E is the exit.
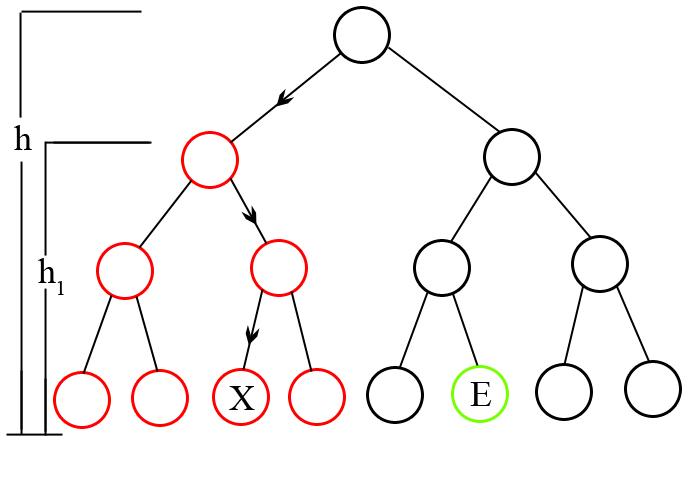
By applying the algorithm we'll reach node X. Both the E and X are in different subtrees of the root. Which means before going to the proper subtree in which the Exit exists we'll have to visit all the nodes of the left subtree (marked in red).
This means we have to get the node which the Exit and the current leaf node X are in different subtrees which will be the least common ancestor (LCA) of the two nodes. Assume the subtree height is h1. This means we visited 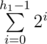 node. By adding the nodes above the subtree which we visited during executing the string for the first time the total number of visited nodes will be
node. By adding the nodes above the subtree which we visited during executing the string for the first time the total number of visited nodes will be 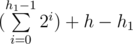 . Now let's go to the other subtree. Obviously we don't need any other nodes except this subtree. So let's do the same we did to the original tree to this subtree. Execute the algorithm until we reach a leaf node, get the LCA, add to the solution
. Now let's go to the other subtree. Obviously we don't need any other nodes except this subtree. So let's do the same we did to the original tree to this subtree. Execute the algorithm until we reach a leaf node, get the LCA, add to the solution 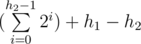 where h2 is the height of the subtree of the LCA node where the leaf node exists. And so on we keep applying the rules until after executing the algorithm we will reach the exit.
where h2 is the height of the subtree of the LCA node where the leaf node exists. And so on we keep applying the rules until after executing the algorithm we will reach the exit.
Also we can do the same operations in O(h) by beginning to move from the root, if the exit is located to the left we go to the left and ans++ and then set the next command to 'R' else if it is located to the right we will visited the whole left subtree so we add the left subtree nodes to the answer 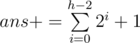 and then set the next command to 'L' and so on.
and then set the next command to 'L' and so on.
Time complexity: 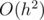 or
or 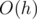
Challenge: What if the pattern is given as an input (e.g. "LRRLLRRRLRLRLRR..."), How can this problem be solved?
Implementation: 9529181
507D - The Maths Lecture
Hint: Dynamic programming problem. To handle repetitions we have to construct the number from right to the left and calculate the answer when we reach a number equivalent to 0 modulo k.
Solution: Let's define 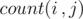 as a recursive functions calculates the number of numbers consisting of n digits satisfying the conditions of the problem and with a specific suffix of length i Si such that
as a recursive functions calculates the number of numbers consisting of n digits satisfying the conditions of the problem and with a specific suffix of length i Si such that 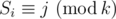 .
.
We want to avoid repetition so by constructing the number from the right to the left when we reach a state with j = 0 with suffix ≠ 0 we return the answer immediately so any other suffix that contains this suffix won't b calculated.
So the base cases are  ,
,  .
.
So state transitions will be 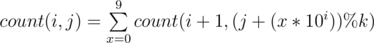 (We add a digit to the left).
(We add a digit to the left).
And we can handle j = 0 case coming from a zero suffix easily with a boolean variable we set to true when we use a digit ≠ 0 in constructing the number.
Time complexity: 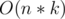
Implementation: 9529210
507E - Breaking Good
Hint: Consider we've chosen a certain path with length d where d is the length of the shortest path from 1 to n and it has x edges that are working. Assume that y is the total number of edges that are working in the whole country. So we need to make d - x changes (to make the malfunctioning edges on the path work) and y - x changes (to blow up all other edges that don't lie on the path). So we will totally make d + y - 2 * x changes where d and y are constants. So the optimal solution will depend only on number of working edges along the path. So we'll have to maximize this number!
Solution: We will use dynamic programming on all nodes that lies on some shortest path. In other words, every node x that satisfies that the shortest path from 1 to x + the shortest path from x to n equals d where d is the length of the shortest path from 1 to n. Let's define Max[x] is the maximum number of working edges along some shortest path from 1 to x. We can calculate the value Max[x] for all nodes by dynamic programming by traversing the nodes in order of increasing shortest path from node 1. So at the end we'll make d + y - 2 * Max[n] changes. We can get them easily by retrieving the chosen optimal path.
Time complexity: 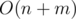
Implementation: 9529272











Problem C can be solved in O(h) aswell :D.
Here is my solution: 9530015
('D' means you are/ you want to go on the right son and 'S' means you are / you want to go on the left son)
Your solution has been added to the editorial. :)
Umm.. thank you :D. I can write a more understandable solution if you want me to :)
My solution also similar I think
507C done in O(h) and challenge part can also be done in O(h) using the similar logic my Solution 9530023
How can you solve the challenge part in O(h) ? According to problem rules if we skip two consecutive commands we move to parent node. For example if the left node is traversed and current input comes out to be LL then we wont move to right node but to parent of current node.
here is my solution in O(h): http://codeforces.com/contest/507/submission/9524186
Algorithm in problem looks like DFS, but in DFS you always search in the left subtree, then in the right. In DFS you'll visit leafs in the following order: 1, 2, 3, ... , 2 ^ h
Here you'll visit leafs in different order.
So you only need to understand how to calculate this bijection in O(h).
And then you can simply calculate the answer.
Yeah i get. I too did it that way. Solution
I was asking for the challenge part of Problem 507C which i think is removed from the post now.
Challenge: What if the string is given as an input (e.g. "LRRLLRRRLRLRLRR..."), Can this problem still be solved in O(h2)?
You can see my comment where I explain my algorithm to solve the problem. Taking L analogous to 0 and R analogous to 1 we can convert to given input string to "011001110101011..." That means the leaf which is ("011001110101011...")in base two, will be the first node to be visited and in any place where the pattern does not match, we would add 2^(h-i) for each iteration so as to mark the nodes as visited (i being the index from the left side of the binary string). This would help us to solve the problem in O(h) time.
I guess this solves the proposed more general problem too. Can you explain how to compute the bijection in O(h)?
Thanks a lot... I have find my solution.
Problem E could be also solved with a bfs to mark the level of each node, and a dijkstra from node n to node 1, following the bfs tree, with cost of edges 0 or 1. It's time complexity is O(|E| * log |E|), but it's still good enough.
Why so much negative votes? It is just how I've solved it :/
Yes, really, why so much negative votes? It's a good solution I believe.
An interesting round... though I nearly solved E...:P (but failed in the end...T T)
Finally blue :) Yay!
Has someone tried to solve problem C "backwards"? As in generating it's path back to the root? Couldn't you calculate the answer as move up to the root summing up the size of subtree rooted at it's sibling (in case it's sibling happens to be visited first with the given traversal in the problem statement)? Also, is valid to consider that it's sibling is visited first only if the actual node we're currently on has the same parity (odd or even) as it's father (if you label them from 1 to 2^h+1 from left to right as you move to lower levels of the graph)?
I hope I made myself clear, any ideas are welcome.
It seems like this approach was also valid or at least I managed to get away with it with the test cases, haha! Code : http://codeforces.com/contest/507/submission/9532476
Problem C can be solved in O(h) time. This was a really good question and my approach is stated below. The problem first requires you to convert (n-1) to its binary form (we took n-1 since we want to number the leaf nodes starting from 0). Next we observe that the binary conversion of (n-1) gives you the location of the node from the parent tree . Example if h=3 and n=6 we want to reach the leaf numbered 5 (taking 0 as the starting first leaf).
Converting 5 to its binary form, we get 101 What the number 101 tells us is that we reach this node by taking the path R-L-R. We then observe that the first element tells us if we have to take a right. But according to the pattern given we must traverse the left side of the tree. This would consist of (2^h)-1 (number of nodes on the left part of the parent node) nodes and 1 node (the parent itself). So in the first step we add 2^h to the number of nodes visited.
Now, we look at the next bit. In the previous step, since we already took a right we should take a left according to the guessing pattern given in the question. Even in the RLR pattern we observe for the number 5, we have to take a L so we mark the present node is visited by adding only 1 this time. This process continues till you reach the leaf of the tree.
To get a better understanding you can see my code in the link shown(I have written the necessary comments to help make it easier to read my code) http://codeforces.com/contest/507/submission/9531335
Now answering the challenge question to C if we want to solve the question for "LRRLLRRRLRLRLRR..." We repeat the process by converting n-1 to its binary form and proceed with the above algorithm by taking the new string into consideration. A pointer to the present index of the string would suffice. Thus, we can solve the challenge question in O(h) time as well.
I did that one too. About challenge: if you have visited only the left of some node and next commands are LL you have to go back up by-passing the nodes on the right of that node. i think this approach will fail on a case like that.
tourist has a much simpler implementation for your solution. Check this: http://codeforces.com/contest/507/submission/9517954
Green again :-)
O(h) Gentle solution of С using bit manipulation in Java:
In problem E: how can we find the shortest path from 1 to x and the shortest path from x to n in time?
By pre-calculating two arrays D1[x] which means the shortest path from node 1 to node x and DN[x] the shortest path from node n to node x.
but how can we precalculate them?
Just do two BFSs. One from node 1 and the other from node n.
thanks, got AC.
For problem E, I have another solution.
My solution: 9530019
I also solved it by this way =)
Here is my solution: 9533709
P.S I think that this problem E is much easier than "usual" problem E on CF.
can any one tell me what is wrong with my solution to problem D ??
http://codeforces.com/contest/507/submission/9533089
I didn't understand the idea for problem D. How did you come up with such solution? I have an idea for the problem though it didn't produce the right answer right from test #3. Let's define dp[i] the number of suffixes y with length i such that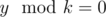 and there is no true suffixes of y that divides k. Also we define cal[i][j] as suffixes y' with length i and
and there is no true suffixes of y that divides k. Also we define cal[i][j] as suffixes y' with length i and 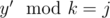 . Also all suffixes y' have no suffix that divides k.
. Also all suffixes y' have no suffix that divides k.
First we calculate cal[1][j] by trying out all numbers from 1 to 9. Then set dp[1] as cal[1][0] and we set the base value cal[i][0] = 1 (0 only). Then, for general i, j we shall have
(P[i][j] = number of indicies of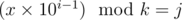 )
)
Therefore the answer will be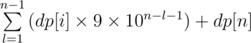
Of course, all of them would be modded by m when actually coded. Please correct me if i'm wrong. Thank you all!
I don't understand your transition for cal[i][j]. Why don't you calculate cal[i + 1][...] from cal[i][...]? It seems easier to me. You set the first digit for the i + 1 digit number (from 0 to 9), the current modulo (which must be bigger than 0 so that we don't count suffixes more than once) and calculate the resulting modulo. Something like this...
I understand pow(10,i)*d is to set the 1st digit num, but what if j>=pow(10,i)*d or at least they have the same digit? Besides, can you explain a little bit why suffixes are counted more than once if modulo==0?
It doesn't matter because in that case DP[i][j] would be 0, so it won't alter the answer.
We'll be counting suffixes more than once if j = 0 in that code above, because we'll potentially be using the suffixes of the current length to build future longer suffixes. For example, consider K = 3 and the suffix 36, which is a multiple of K. If we set 4 to be the first digit of the next suffix (j = 0, d = 4 in the code above), we will get a number which is modulo 1 (436). If we then use this modulo 1 number to build a 4-digit number with 5 as the first digit (j = 1, d = 5 in the code above), we will get number 5436, that is modulo 0 but contains 36 as a suffix, which we already counted earlier. That's why we only consider j in the range [1, 9] in our code.
Thank you OwO ~~ . Yes after some thinking I finally found out that my solution is really really weirdly and complicatedly implemented >_> . Still I have a lot to learn 3.3~~ Also, isn't it better for us to pre-calculate all
pow(10,i)s instead of putting it straight into code @.@ ?It seems you can not is considered that y > 0.
And optimization:
cal[i][j] = sum x = 0..9 cal[i - 1][(j - x * 10 ^ (i - 1)) mod k]better thatcal[i][j] = sum l=0..k-1 p[i][l] * cal[i - 1][(j - l) mod k](first O(10), second O(k))The y > 0 condition is calculated by setting all cal[i][0] = 1 (we only allow solutions x00000..0 to exist). All others we ignored by not applying the j = 0 calculation into cal[i][j] calculations. There should be no problems with that `~` And yes, thanks for your optimization!!~~
Why count(n,0) = 1 in 507D? There are more than 1 n-digit number divisible by k aren't there?
yeah i totally agree, count(n,0) is not always equals to 1
"for every certain suffix"
This is he answer for every unique suffix with length n as I'm calculating the answer recursively from the right to the left.
I did not understand how you derived your state transitions and how it does not count sub-problems more than once. Also what exactly is the deal with j = 0 and the boolean variable? Kindly elaborate!
I've enhanced the editorial for D. If you have any problems kindly ask.
Thanks! I gained a little more insight but still have one doubt. How do we compute the final answer using the notations you have given?
If count(i, j) gives us the number of numbers of length n such that a suffix of length i leaves remainder j, then according to me the answer should be summation over count(i, 0) where i varies from 1 to n.
But you say that count(n, 0) = 1 "for every certain suffix". What does that mean? From the notation given, I am interpreting that if k = 1, then for count(n, 0) the answer should be 9 * 10^(n-1) and not 1 like you say.
Kindly resolve my mistake :)
The answer will be count (0, 0) :)
As I said the function counts only the result of the digits that is located to the left of i as we are constructing the number from the right to the left.
Consider a case where the number generated so far is 12345 where n = 10 function count (5, 12345 % k) will count the number of combinations XXXXX12345 that satisfies the problem's conditions.
So by default a number like 1234512345 if it's equivalent to zero modulo k then count (10, 0) will be 1 an there is only one combination of the number.
Got it! Thanks a ton! Btw is there any iterative approach as well?
Yes!
We can easily convert the approach into an iterative one:
And the answer will be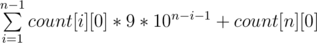
Thanks!!!
Won't there be repetitions?
Because, count[i][0] is actually measuring the number of suffixes of length i which are divisible by k, and we are adding all possible numbers before it, so it would also include any number with suffixes greater than size i, say j. And, because we add number with suffixes of length j also, same number would be included multiple times.
For Example, for n = 2 and k = 3,
33 would be included for two times.
One time in 9 * count[1][0], Second time in count[n=2][0].
Please let me know where am I wrong.
Note that in the second loop j is starting from 1 so that we will not count the case where the suffix equals zero.
So count[2][0] won't have count[1][0] in it.
Thanks! That clears!
Why doesn't the middle loop run until j<=(k-1) ?
I think my approach is the same iterative idea...can someone tell me why it does not give correct answer :(
9909747
Edited: nvm...I found the problem..! :)
Why is j<k-1 in the middle loop and not j<k?
How is it handling the condition of suffix not getting repeated?
The one problem that i face is that i am unable to calculate the square root of the number in gcc(compiler). math.h file contain the function but math.h cannot be linked to code. how to resolve that problem i want to look at the solution which are submitted by the other in c.
when you are running add the -lm flag on your compile command e.g. gcc -o exe filename -lm
I think CF runs its compilers with the flag , even if not math.h links properly
I didnt understand the purpose of binary search in 507-B solution link provided in editorial...can anyone please explain...as suggested in editorial, we could have simply got the answer by ceil(dist/2*R).
binary search is to find optimal number of moves, in each iteration it tries some value x as number of moves and checks whether the distance is covered or not and tries to find minimal x that covers the distance.
It's to avoid precision errors.
If the limits were up to 109 even solutions that used double datatype would fail.
can anyone elaborate on the solution of problem D-the maths lecture...
Here's really simple solution for problem C: http://codeforces.com/contest/507/submission/9522115 (in O(h))
very bad round the problems were easycoding and not interesting
In problem E — we actually don't need to know whether some node lies on shortest path or not; there are also different possible solutions with Dijkstra's algorithm described in comments, but you also don't need it. Solution with a single BFS sounds simpler.
Here is the idea — you can calculate values of dynamic programming right inside this bfs. If you'll store number of bad edges in shortest path to given vertex, along with length of this path — you will have answer for a problem after running single bfs from vertex 1 to vertex n.
My solution 9516327 from a contest works this way.
Actually I had a solution combining both bfs and DP but in O(m log m) using a priority queue but your solution looks simpler. :)
Nice :)) thanks a lot:))
I think the complexity of problem D is O(n*k*10)
In big O notations we get rid of constant factors.
Oh, I forgot that. :(
Sorry for my mistake.
What's the use of boolean
changein 9529210 (D-Maths Lecture). I think it's used just to check that do we have atleast one non-zero number in the suffix so far?.Also the condition
if(ind == n || (rem == 0 && change)) return 0;can beif(ind == n) return 0;. because if(rem==0&&change) is truewe must have alreadyreturn-ed from above.Can I categorize it as Digit-DP?
Yes.
I don't know actually I think I wrote it while testing something. @_@
Yes.
I have difficulty comprehending
Can someone explain to me what this means?
a detailed example of the construction process would be very appreciate.
507E Use 2 BFS one from 1 and other from n,mark the valid vertices then use 0-1 BFS.
Use double instead of float in B.... I was getting WA in test case 37..just saying if someone does the same in future.
Can you pls say why ?
I think I have a unique solution for c P.S. I didn't read the editorial yet.. hope I didn't waste your time