I was looking at the editorial for Round #300 Problem F, where you needed to count how many elements in a range is greater than k. The editorial stated "online data structures for this type of query are rather involved" and proceeds to describe a solution using the simpler Binary Indexed Tree.
Is there any known data structure that can efficiently query "how many elements in this range is greater than k"?











Segment Tree. In vertex we store sorted subarray using std::vector. Than, for find count of elements in segment [l, r] greater then k, we can do upper_bound in each of log(n) vertex, so complexity is O(log^2(n)) per query.
with using fractional cascading it can be reduced by nlogn fractional cascading
If there is no update queries, persistent segment tree will do. per query.
per query.
Also, if you solve problem in offline BIT is enough.
What if there are updates ?
You can do it in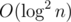 with segment tree which keeps the full interval in each vertex then.
with segment tree which keeps the full interval in each vertex then.
u can also solve this problem using SQRT decomposition :)
you can also solve this problem using trie. I solved a similar problem using this approach where u need to find number of elements in range(l,r) which are <= k in each query.
How ?
We can build a binary trie tree where at each node we store a vector containing the index of element of which that node is a part of.
For example we want to insert
arr[10] = 5andarr[11] = 2in the trie. Let us consider all the elements in the array fits in 4 bits at max. So5 = b(0101)and2 = b(0010)in binary. We can build a trie like following inO(log2(maximum arr[i])).Now for the query portion i.e. finding number of elements greater than k in range l to r, what we can do is to count the number of elements less than or equal to k and then subtract it from total number of elements in range l to r to obtain our output.
If we start traversing the binary representation of k from most significant bit to least significant we find the if ith bit of k is set then all the elements in trie with ith bit unset are less than k. So we can add the count of all indexes in the range l to r to the answer.If ith bit is unset then all elements with ith bit set are greater than k, so we ignore those elements. Following is a recursive function implementing the above idea.
Here
total(v)counts the number of elements>= l&&<= rin the given vector v. It is defined as :upper_bound(v.begin(),v.end(),r) - lower_bound(v.begin(),v.end(),l)Finally you calculate answer as :
r - l + 1 - cnt(root,l,r,k,(1<<30))))assuming maximum element in array to fit in 30 bits.For contests, If you need a good abtraction or if you want to learn a new merge-sort tree based datastructure for certain class of problem, Check this