560A - Currency System in Geraldion
If there is a banlnot of value 1 then one can to express every sum of money. Otherwise one can't to express 1 and it is minimum unfortunate sum.
It is easy to see that one can snuggle paintings to each other and to edge of board. For instance one can put one of painting right over other. Then height of two paintings equals to sum of two heights and width of two paintings is equals to maximum of two widths. Now we can just iterate orientation of paintings and board.
559A - Gerald's Hexagon & 560C - Gerald's Hexagon
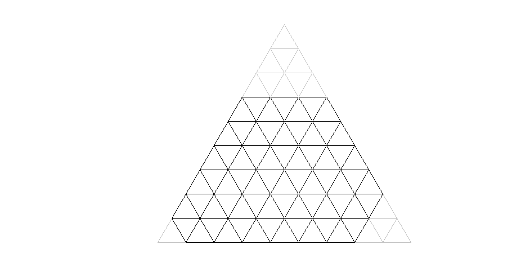
Let's consider regular triangle with sides of k Let's split it to regular triangles with sides of 1 by lines parallel to the sides. Big triange area k2 times larger then small triangles area and therefore big triangle have splitted by k2 small triangles.
If we join regular triangles to sides a1, a3 and a5 of hexagon we get a triangle sides of a1 + a2 + a3. Then hexagon area is equals to (a1 + a2 + a3)2 - a12 - a32 - a52.
559B - Equivalent Strings & 560D - Equivalent Strings
Let us note that "equivalence" described in the statements is actually equivalence relation, it is reflexively, simmetrically and transitive. It is meant that set of all string is splits to equivalence classes. Let's find lexicographic minimal strings what is equivalent to first and to second given string. And then check if its are equals.
It is remain find the lexicographic minimal strings what is equivalent to given. For instance we can do it such a way:
String smallest(String s) {
if (s.length() % 2 == 1) return s;
String s1 = smallest(s.substring(0, s.length()/2));
String s2 = smallest(s.substring(s.length()/2), s.length());
if (s1 < s2) return s1 + s2;
else return s2 + s1;
}
Every recursive call time works is O(n) (where n is length of strings) and string splitten by two twice smaller strings. Therefore time of work this function is 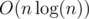 , where n is length of strings.
, where n is length of strings.
559C - Gerald and Giant Chess & 560E - Gerald and Giant Chess
Let's denote black cells ad A0, A1, ..., Ak - 1 . First of all, we have to sort black cells in increasing order of (row, column). If cell x available from cell y, x stands after y in this order. Let Ak = (h, w). Now we have to find number of paths from (1, 1) to Ak avoiding A0, ..., Ak - 1.
Let Di is number of paths from (1, 1) to Ai avoiding A0, ..., Ai - 1. It's easy to see that Dk is answer for the problem. Number of all paths from (1, 1) to (xi, yi) is 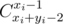 . We should subtract from that value all paths containing at least one of previous black cells. We should enumerate first black cell on the path. It could be one of previous cell that is not below or righter than Ai. For each such cell Aj we have to subtract number of paths from (1, 1) to Aj avoiding black cells multiplied by number of all paths from Aj to Ai.
. We should subtract from that value all paths containing at least one of previous black cells. We should enumerate first black cell on the path. It could be one of previous cell that is not below or righter than Ai. For each such cell Aj we have to subtract number of paths from (1, 1) to Aj avoiding black cells multiplied by number of all paths from Aj to Ai.
We have to calculate factorials of numbers from 1 to 2·105 and inverse elements of them modulo 109 + 7 for calculating binomial coefficients.
We can use Pick's theorem for calculate integer points number in every polygon. Integer points number on the segment between points (0, 0) and (a, b) one can calculate over GCD(a, b).
Integer points number in some choosen polynom is integer points number in basic polynom minus integer points number in segmnent of basic polynom separated by every segment of choosen polynom.
Let consider every potencial segment of polygon. We can calculate integer points number in his segment and probability that we will meet it in choosen polygon.
Probability of segment AiAi + k is 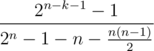 . Let use note that we can calculate only segments with k < 60 because of other segmnet propapility is too small.
. Let use note that we can calculate only segments with k < 60 because of other segmnet propapility is too small.
Lighted part of walking trail is union of ligted intervals. Let's sort spotlights in increasing order of ai. Consider some lighted interval (a, b). It's lighted by spotlights with numbers {l, l + 1, ..., r} for some l and r ("substring" of spotlights). Let x0, ..., xk is all possible boundaries of lighted intervals (numbers ai - li, ai и ai + li).
Imagine, that we know possible lighted intervals of all substrings of spotlights. Let left[l][r][j] is least possible i such that set of spotlights with numbers {l, l + 1, ..., r} lighting [xi, xj].
With left we can calculate value best[R][i] maximum possible length of walking trail that could be lighted using first L spotlights in such way that xi is rightmost lighted point. It's easy to do in O(n4) because 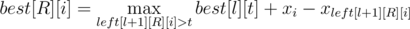 .
.
Now all we have to do is calculate left. Consider some substring of spotlights [l, r]. Let all spotlights in the substring oriented in some way lighting some set of points. We could consider most left (i) and most right (j) lighted points, and left bound of first lighted interval (t). If set of lighted points is interval t = j. Consider how all the values change when we add spotlight r + 1 and choose its orientation. We have new lighted interval [a, b] which is equal to [ai - li, ai] or [ai, ai + li]. Now most left lighted point is min(a, xi), most right is max(b, xj). Right bound of leftmost lighted interval does not changes if a > t or becomes equal to b, if a ≤ t.
Not for each L we can calculate dp[r][j][y] least possible i that it's possible to orient spotlights from [L, r] in such way that xi is most left lighted point xj is most right one and right bound of leftmost lighted interval is xt. Thet it's easy to calculate left[L][][]. That part is done in O(n4) too.










thanks ;)))
From comments on the original blog I believe that simple simulation in Div1 B passes the tests, is there a proof that this is faster than O(N^2) or are the testcases just weak?
Additionally, my solution for Div1 C is stupid, but works in O(N^3) — and passes in 1700ms. Is this again the result of weak testcases or are the graders just crazily fast?
P.S.
My O(N^3) seems to be O(N^2)...
Not only brute — force string comparing gets AC, but also hashing gets TLE.. What's wrong?
Mine also TLEd on Test Case 89 and I used hashing.Can't figure out why it's so. :(
Same Here
mine too...getting tle on test case 89...even though i didn't use any hashing ...can anyone tell why is it so?..this is my submitted solution.. http://codeforces.com/contest/560/submission/18525371 .. any help would be appriciated
Even O(NlogN) suffix array and O(1) for each comparison gives TLE. First I thought "cin" might be the reason but "scanf" version (submitted after contest) also gave TLE.
http://codeforces.com/contest/559/submission/12186704
It's because the time complexity of your solution. In each recursive step you can make up to 4 recursive steps which gives you O(n2) overall complexity even though you have O(1) for comparison.
However, if you shuffle your recursive calls as in 12187657 you have a better performance since it's hard to build a test case that requires all 4 calls in each recursive step.
Can you find any fault with my submission. Link is in another comment downwards on this page.
Consider this : http://codeforces.com/contest/559/submission/12184235
EXACTLY same recursion. Just the "equal" function now compares in trivial O(n) time. It passed the same test case in 31ms where the first one gave TLE. I don't think the recursion is a problem...!!
yours are exactly correct,but the invariants are too large~~~
I have also got TLE in Testcase 89, then I suffled, then in testcase 91 then again suffled and accepted.
plz post yr accepted solution too..
Is it really hard to make a test case where two strings are not equivalent? I don't think so!
It's definitely super easy to make a test case where two strings are not equivalent. My point is that taking into account the short circuit evaluation of boolean expressions compilers use, it's hard to create a test case where all 4 recursive calls are made for each step since you are choosing randomly the order you use to make the recursive calls.
The worst case scenario for this problem is when the answer is "NO", but for a "NO", I have used a counting table (counting the frequency of each character) preprocessing each segment to make sure it is not a NO, so It passed the time limit.
Ah yes ofcourse. I understand now.
Can you explain to me what it has to be done WHEN WE CAN'T DIVIDE a string IN TWO EQUAL SUBSTRINGS? From this editorial I understand that is ok if it can't be divided,but from problem statement it sounds that it isn't ok ..... My solution was good but I print NO when it cannot be divided equally,maybe that's why....
This just came to my mind. Please review and comment errors.
If you think of the recursive comparing as a tree, for each depth, the length you have to compare gets twice, but you have to count half the time. So each level you have to compare O(N) tume, which results in O(NlgN) time complexity.
Well, if we assume that every state (from_a,to_a,from_b,to_b) is computed constantly we call 4 recursions from each state. Let's say that N=2^K, so K=log2(N).
How many times are we going to divide a string into halves? It's K times.
And each time we call 4 recursions so it's 4^K which is 2^K * 2^K or N^2.
Do I miss something? When I was given this problem I coded this solution and got TLE but I thought I got a fast solution and then perchema told me why it's N^2. I asked the teacher who gave me the problem if she could find the link to the problem and if she find it, I will give the cases which made my solution exceed the time limit (of course, I can be missing something, so tell me if something is wrong with my arguments).
At C you only call solve(k-1,x) so it is N^2.
Actually,someone i know proves that the complexity is O(n^1.57)
If A and B are equivalent, it will only recurse at most three subtasks so complexity is T(n) = 3T(n/2) that is approximately O(n^1.57)
If A and B are not equivalent, it will recurse four subtasks only if two subtasks are equivalent so complexity is T(n) = 2T(n/2)+O(n^1.57) it's also O(n^1.57)
EDIT1: I made a mistake to let T(n) = 3T(n/2) in the first case since the subtasks might not be equivalent ! But after further calculations i still believe the complexity should be O(n^1.57) Plus, i wrote a program to calculate the times of recurses and it's about 10^9 which Codeforces is still able to run in 1s
Which of these problems are well known or not unique?
There's a comment in original blog
I am sure for Div1 B. A link for Div1 C was provided by someone in the announcement and another user wrote that Div1 A is also known...
For Div1B I used this kind of hash (and it passed the systests):
Where F is some simple pseudo random mapping, H1 and H2 of odd-length block is just some string hash.
Then I just compare (H1(s1), H2(s1)) and H1(s2), H2(s2)).
Can it be hacked? Intuitively, (H1, H2) is a hash of an unordered pair. It's easy to see that this algorithm works for YES cases. But I don't know how to (dis)prove it for NO cases.
Why did you used H2? H2 itself fails test
But I can't see how to make H1 fail. It didn't work without H2?
UPD: I like your approach :)
H1 fails test:
(because a+d=b+c).
Though I think F(H(a) + H(b)) may be enough if we use a little more advanced hashing for strings (e.g. such that it's hard to find a, b, a', b' such that H(a) + H(b) = H(a') + H(b').). Since we already use similar F, we can apply it to the output of the polynomial hash.
Submission
Div1 A was awesome! Cheers!
very awesome, just open search engine and u have answer
Can you give google search query?
sum1 asked this question here http://math.stackexchange.com/questions/1370494/how-many-triangles-in-a-irregular-hexagon
Thanks -NE0-. I would appreciate if you can provide me the google search query, I want to know what I was missing.
In problem B/Div1. If we use Rabin Karp algorithm to match substrings then we can do this in O(n). Am I right? bool check(s1,s2) { if(s1==s2) return 1; else return (check(s11,s21)&check(s12,s22)) | (check(s11,s22) &check(s12,s21); }
Your algorithm is O(n^2). You can do it in 3 (instead of 4) sub checks and it will be O(n^1.6). Another solution is to find the lexically smallest reachable string for both of the strings and compare, complexity O(n logn).
3 comparison also passes
Everything passes here... -_-
When it's string, things do happen and many find their own way...
But I'm pretty amazed at the editorial's solution. Thanks.
Prob D/Div2: Can somebody help me understand why this code gave TLE on test case 89? I used hashing to check if two substrings are equal.I think that the solution should run in O(N).
(http://codeforces.com/contest/560/submission/12185587)
Edit: Apparently I just reversed the order of condition check in my code and it got accepted. Still can't figure out this bizarreness.
84 99
82 54
73 45
Gerald is into Art how is the output on this test case YES
45 + 54 == 99
max(82, 73) < 84
My solution for div1 B is the naive one with an additional check: two strings can only be equivalent if they have the same characters. I thought this way the function would call itself recursively at most three times, but I don't know if this correct.
My code: http://codeforces.com/contest/559/submission/12177788
Can anyone help me correcting this submission 12184498 ? I was using recursive checking of equivalence. I think the complexity is O(n log n) Anyway, the verdict is TLE on test 6 :-? I have no idea why... Thank you.
You didn't check for simple string equivalency if the string had an even length.
I had a similar algorithm, but mine died on test 91 :(
http://codeforces.com/contest/560/submission/12177681
EDIT: stargazer (above)'s solution incorporated checking for differences in letter frequency, which would speed this up enough to make it pass.
EDIT #2: Apparently you don't even need any tricks to make this method work. You just have to lower your constant time, possibly by using char arrays and pointers.
Could you show some more detailed calculation why k<60 suffices (in Div1D)? I set k<=120 and I would feel very insecure lowering it even more. Demanded probability is pretty high, (1e-9) and there can be 4e18 points in our polygon and we use ~1e6 operations, so it looks that to be safe we need to set k to at least 120. That was actually pretty important for me, because I was struggling for half an hour with TLE, replacing 120 by 60 would really help me :d
Congrats international grandmaster! :)
I guess we care about area calculating, not about border points? Probability of getting polygon with two consecutive points (neighbors) that were distant by at least K in original polygon is O(N * 0.5^K). We can expect that such polygons have (in general) area lower than those we consider. I think it's true that for big N average area of bad polygons is lower than average area of not-bad polygons. So we have error at most O(N * 0.5^K).
Why O(N * 0.5^K)? For every point there is prob. 0.5^K (or sth like 0.5^(K+2)) that it's in a polygon and next K points aren't. So we have at most O(N * 0.5^K) for a bad polygon.
Can some one help me out here http://codeforces.com/blog/entry/19374
How to avoid cacellation in div1-D? I found a case that cause big error (>2e-8) on many accepted submissions.
(correct answer is 37150746.00)
I think the test cases of system test is very weak. Can one even solve in a language that has no long-double?
Which cancellation are you talking about? I have one subtraction (area — border points), but I handle it on integers. Maybe some people did it on long doubles (as I did firstly, but changed that due to getting TLE), is that your point?
Calculation with signed area causes cancellation. Calculation of
area - boder pointscan cause cancellation as well.Ah yes, of course just area alone is 'cancellation bottleneck' :).
Irrelevant: What is the reason for your weird submission times today :P?
"00:00:00 Participant has been assigned to the room (assigned to) 18 01:35:51 D Accepted [main tests] 01:36:06 C Accepted [main tests] 01:36:20 B Accepted [main tests] 01:47:14 A Accepted [main tests]"
Did you lost your Internet connection? You're not from North Korea, so I won't accuse you of cheating :D
I hestitated for whether I participate until 1:35. So, I had written code of B, C and D. I was really idiot about that. That simply decreased score and rank. If I have normally participated, I could get ~5th I think.
I'm offensive and I find this North Korean.
Strange — my solution (with doubles in C++) calculates signed area (the usual cross product stuff) and subtracts border points from it, but it doesn't fail on this case.
I see how you could replace most of the calculation with whole numbers (the probability depends only on distance which is <80, so you can have an array of 80 long longs and only sum them up in the end), but not all of it.
Problem E div1 has a solution within O(n^3).
12187399
It is based on calculating DP d[i][j][t], where i is number of concidered projectors (numbered in increasing order of their position), and (j, t) encode the furthest enlighted point (j <= i is number of projector, 0 <= t <= 1 is where it is oriented).
That is nice! It's even easier to implement than our approach.
Suppose we are on projector i , and we know that furthest enlightened point is enlightened by the jth projector with the orientation t. Then as you said the maximum enlightened length will be equal to dp[i][j][t], right ? Let's say we are deciding on the ith projector. Can you please explain how do you calculate the length that is enlightened after placing the ith projector facing the negative direction ?
the transition is more complicated. it considers placing several projectors. you can read the code to figure it out
Also vepifanov just explained me his solution 12204272 which works within O(n^2) !!!
Sorry if it sounds silly, but how do you know in Div 2 A, that if there is a value 1 then one can express every sum of money. I understand that given a set of values, the combinations of those values goes from 1 to sum(n values), from there I have to check which is minimum and if there is none print -1, can someone explain why the solution of the editorial?, what I am missing?
"Of course, they can use any number of banknotes of each value."
If you have a banknote of value 1, for each value N, you always can reach N using N banknotes of value 1.
Ah I see, thanks for answering, but what about if only you have 2 and 3?, just numbers multiples of 2 and 3 and sum of those values?
I can't get what you say clearly .. but If you have only 2,3: you can't get the sum to 1, and the the min unfortunate will be 1 !
Thanks for answering, I think I have to read again the problem statement, what I was trying to say that it is not possible to get 1 if you only have 2 and 3, so It is always 1 if there are not any 1
You're welcome :)
2C becomes really simple if you add equilateral triangles on two opposite sides of the hexagon.
Could someone please tell me what's the complexity of this code?
Submission: 12188672
It seems its O(n*logn*logn).
Why this approach don't work for Div1C
Because 10^10 operation is a little more than codeforces invokers can perform in 2s.
Say range is 1000*1000 then it will be logically correct? Right?
I think it's not, but I don't understand what arrays row and col means.
row and col are the blocked index. Say for the first case, we had block at 2 2 and 2 3. So, row [2] = true and col [2] = col [3] = true .
So, if you want to block (2, 2) and (3, 3), you have to block (2, 3) and (3, 2).
Links to problems don't work
I got an stupid but practical solution for Div1 A: We can just get the coordinate of the six points easily. And we can use the cross product to get the area of the hexagon. Let's define it as Area. And the answer is 4 * Area \ sqrt(3). Nevertheless, we should pay more attention to the decimal precision.
Yeah,I did it in the same way.... I failed to find a better solution.... But this works!
Could you please explain how to find the coordinates of all point??
http://codeforces.com/contest/560/submission/12178333 a bit of math. draw on a piece of paper and you'll find it clear.
For Div2 E, how would you compute binomial coefficients?
You have classical formula . So, all you have to know is factorials of integers from 1 to 2·105. Then
. So, all you have to know is factorials of integers from 1 to 2·105. Then 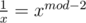 modulo mod (if mod is prime), so Cnk = n!·(k!(n - k)!)mod - 2 modulo mod. So, you should calculate a! and (a!)mod - 2 for a from 1 to 2·105 and then find binomial coefficients in O(1).
modulo mod (if mod is prime), so Cnk = n!·(k!(n - k)!)mod - 2 modulo mod. So, you should calculate a! and (a!)mod - 2 for a from 1 to 2·105 and then find binomial coefficients in O(1).
Thanks for the help!
I found some English words which can't be found in dictionaries....and I don't understand some sentences.....
I tried reading editorial to Div1E, but it gave me an English cancer >_>. It's really hard to achieve given my knowledge of English :x.
Moreover "Consider some lighted interval (a, b). It's lighted by spotlights with numbers {l, l + 1, ..., r} for some l and r ("substring" of spotlights)." on the very beginning seems very suspicious. Why do we assume that an interval is lit by an interval? In general it looks it's very far from true.
My English is one big shame, yep. In that sentence I meant that if (a, b) is maximal lit interval and spotlights i, j lies in (a, b) and i ≤ k ≤ j, then interval lit by k is subset of (a, b). I missed the word "maximal". Is it obvious now?
In div1B/div2D, how does finding lexographic minimum equivalent string to A and B and ensuring that they are equal result in A and B being equivalent? Is there any proof for this?
Let us note that "equivalence" described in the statements is actually equivalence relation, it is reflexively, simmetrically and transitive.
It means that if we create new string from string a and call it b, we can change it back to string a using the same criteria.
And we find lexicographic minimum equivalent string to make compare two strings easier.(if you want, you can find lexicographic maximum XD)
But why should the lexographic minimum/maximum equivalent string for A and B be equal for A and B to be equivalent?
We can say that we sort string a and string b and just compare it:
If(smallestEquivalent(string a)==smallestEquivalent(string b))cout<<"YES";
else cout<<"NO";
An equivalence relation on a set (one which is reflexive, symmetrical and transitive) divides it into non empty equivalence classes, in each of which every two elements are equivalent. Since EVERY two elements of an equivalence class are equivalent, we can say that A and B are equivalent (= are in the same class) if and only if A is equivalent to C and C is equivalent to B for any arbitrary C in their equivalence class. The set of strings of finite length under lexicographical order is a linear/total order (actually a well order which is stronger), and applying this order to each of the equivalence classes, we can uniquely (every non empty subset of a well ordered set has a least element) select C for each of the equivalence classes to be the least element in respect to the lexicographical order. The strings equivalence relation (the one in the problem statement) is indeed an equivalence relation, and therefore the above property holds.
Got it.Thanks! :D
Dhruv, do you mind explaining it to me? I didn't get it. Also, why are people above talking about using hashing ? I don't see a need for it. Thanks
I didn't get to put from "The set of strings under....". Can you please explain?
In div1/E can somebody explain how to get 5 in 1st test case because I've been trying to figure it out for the last 0.5h and I keep getting 7. Here is my though proces:
3
1 1 iluminate segment [0,1];
2 2 iluminate segment [2,4];
3 3 iluminate segment [3,6];
And then the segment that is iluminated is [0,6] and it has the size 7. Please tell me what am I doing wrong.
No, you have illuminated segment [0, 1] and segment [2, 6]. Summury you illuminated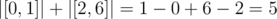 .
.
Indeed you're correct I'm just being a pudding-brain.
Thanks sir!
for problem Div2 C, Gerald's Hexagon.
for the 2nd sample test case
1 2 1 2 1 2the answer turns out to be 4 if we use the formula
(a1 + a2 + a3)^2 - a1^2 - a3^2 - a5^2.Can someone please explain that?
a1 = 1; a2 = 2; a3 = 1; a4 = 2; a5 = 1; a6 = 2
(a1 + a2 + a3)^2 — a1^2 — a3^2 — a5^2 = (1 + 2 + 1)^2 — 1^2 — 1^2 — 1^2 = 16 — 1 — 1 — 1 = 13
Even if we use 0-indexation:
a0 = 1; a1 = 2; a2 = 1; a3 = 2; a4 = 1; a5 = 2
(2 + 1 + 2)^2 — 2^2 — 2^2 — 2^2 = 25 — 4 — 4 — 4 = 13
Profit
ohh yes.. thanks a lott
actually I messed up in the code with indexing.
Do you have proof for the problem?
For problem "Gerold And Giant Chess", is this approach correct?
if([i-1][j] is not a black cell) NoOfWays[i][j] += NoOfWays[i-1][j]
if([i][j-1] is not a black cell) NoOfWays[i][j] += NoOfWays[i][j-1]
And final answer being NoOfWays[1][w]
What size of array "NoOfWays"?
[h+1][w+1]... Basically NoOfWays[i][j] stores NoOfWays to reach i,j from h,1 ...where h,1 is the top left corner..
And NoOfWays[h][1] = 1, is the initial condition
And how big is (h + 1)·(w + 1)?
Ya I get it that there will be memory limit exceeded. Check my comment below...I manager using only an array of [2][w+1] bt still getting a wrong answer.
Is this approach correct?
No, your still have TL while doing O(n2) operations
Let's calculate necessary memory
NoOfWays — int array [h+1][w+1]. So, it has size 100001*100001*4 bytes = 400080004 bytes ~ 390703 kilobytes ~ 381 megabytes > 256 megabytes (Our memory limit).
Actually you have around 4·1010 = 40Gb.
Ohhh.... I'm not good in math:D
Sorry for misleading)
Can someone please tell me why this code fails on testcase #5 for 560E-Gerald and Giant chess.
Code: http://ideone.com/NURs5H
Thanks
Use this testcase:
3 4 2
1 2
2 1
Right answer: 0
Your answer: 722063156
UPD1: hmmmm.... MSVC++ really output 722063156, but GCC output 0... I have no words
UPD2: Found! You have undefine behavior in
ll val = ( ( fact[(bl[i].f + bl[i].s)-(bl[j].f+bl[j].s)]*ifact[bl[i].f-bl[j].f])%mod *ifact[bl[i].s-bl[j].s])%mod;What if (bl[i].f + bl[i].s) — (bl[j].f + bl[j].s) < 0?
1000 1000 2 200 900 1000 1
Right answer: 615121873
Answer on Ideone: 274729474
Thanks :). I found the answer. You have to make sure the previous black cell's column number is less than the current one.
Regarding 560E - Gerald and Giant Chess , We also have to check that the previous column and row numbers are both less than the current one right?
Strictly speaking, less than or equal to.
Some one please explain Div2-D Question? I think i percieved question wrongly... I a just dividing string a into s1,s2 and b into s3,s4. s1 = a[1..len/2],s2 = a[len/2+1...len] (same for s3,s4) and checking whether all characters of ((s1,s3) && (s2,s4)) || ((s1,s4) && (s2,s3)) are equal.
Well, if you understand that "equal" means here not just s1 == s3, but that you should then divide s1 into s11 and s12, s2 into s21 and s22, and check that pairs (s11, s21) and (s12, s22) or (s12, s21) and (s11, s22) are equal (and repeat such dividing until strings length will be odd), then you understand all correctly. (sorry for my english)
In div1-E how can we get answer 13 for test #3?
I would turn everything to the left and we have ligth from -3 to 9, length is 12. How to achieve 13 (it's jury's answer for this test). Do I misunderstood something? Can I treat spotlights as points?
[3, 6]
[4, 5]
[0, 2]
[ - 3, 0]
[9, 14]
Union is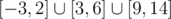 .
.
I get statement wrong. Thanks for help!
What is reverse elemet of fatorial in problem C-Div1?
to clarify, inverse element
In problem B-Div2, gave TLE in testCase 89 with this recurssion:
solve((X1,Y1)&&solve(X2,Y2)) || solve((X1,Y2)&&solve(X2,Y1))
but, when i change to:
solve((X1,Y2)&&solve(X2,Y1)) || solve((X1,Y1)&&solve(X2,Y2))
gave Accpeted
Yeah, it happened to me as well! Do you have any idea why is that happening?
my solution 83219909 got TLE on test case 89, however i just swap the conditions like you and got AC in 83219860.
can you help please !
do you know the reason behind it why this is happening although
a||bis equal tob||aIn problem Randomizer, how can we get the formula of probability of segment A(i)A(i + k) ?
Consider choosing x (x>=3) points from the initial n points, no matter which points you choose, these chosen points make up a convex polygon.
So you have 2^n-1-n-n*(n-1)/2 ways to choose a polygon.
If a segment <A_i,A_(i+k)> is chosen, then any point from A_i to A_(i+k) cannot be chosen. If some point in this interval is chosen, then you are not choosing <A_i,A_(i+k)>, but two other segments.
So you have 2^(n-k-1)-1 ways to choose a polygon. Minus 1 for you cannot choose nothing in the remain points.
Thanks. I got it.
Thanks!
On 1D — Randomizer you said
I didn't understand the sentence. Can someone please explain what that means? Thanks :)
for Gerald's Hexagon question
the number of hexagons is equal to (a1+a2+a3)^2-a1^2-a3^2-a5^2 not its area(^ signifies power)
How is 560A a Geometry problem?
It is not
Please remove this tag.
I can't
In Div2 C how come the area of hexagon is (a1+a2+a3)^2-a1^2-a3^2-a5^2? If we are consider the area of triangle and then deducing the area of smaller triangles then the area of triangle would be root(3)/2 * s^2 where s = side of triangle.
Can anyone tell me why is this giving TLE for test case 89 for equivalent strings problem. I have implemented the same logic as given in the editorial of this question . **** Sahilamin219
[problem:https://codeforces.com/problemset/problem/559/B]
73309702
Because it isn't same logic
Can someone pls give proof for the DIV 2 c question of this round.
excuse me, what exactly you want we to proof?
No need i have got clarified
Interesting phenomenon in the Divide and Conquer solution of Equivalent Strings
Trial 1 : The recursive function is called 4 times.
Verdict : This TLEs at Case 58 . 88646201
Inference : O(n^2) is not good enough
Trial 2 : The recursive function is first called twice to check if Condition A is fulfilled. Only if Condition A fails, 2 more calls are made to check Condition B.
Verdict : This TLEs at Case 91. 88648946
Inference : The first condition is taking most of the runtime.
Trial 3 : The recursive function is first called twice to check if Condition B is fulfilled. Only if Condition B fails, 2 more calls are made to check Condition A.
Verdict : Accepted in 62ms. 88654898
Inference : Inference of Trial 2 is correct. Weak testcases.
Trial 4 : The 4 recursive calls are arranged in the following way in a boolean expression.
if(((Call1) && (Call2)) || ((Call3) && (Call4)))This expression runs 4 times only if
Call2fails. In all other cases it runs 3 times at most.Verdict : Accepted in 46ms. 88655282
Inference : The complexity is around O(n^(1.5)). The boolean logic in the expression makes it a lot faster.
PS : Here Condition A and B refers to the conditions in the question.
How does one prove in Div. 2/D that the given relation is "actually" an equivalence relation? The reflexivity and symmetry seems trivial but I cannot come with a proof for transitivity, nor I can build any intuition strong enough to convince myself.
Sammarize any clarification?
I can do it by induction. Let say we have three strings a, b and c of length n and a is equivalent to b and b is equivalent to c.
let say transitivity holds for length n-1. Now we want to prove for length n.
Now say a1 is Eq to b1 and b1 is Eq to c1 then a1 is Eq to c1 (length n/2 < n-1)
Similarly, a2 is Eq to c2 hence a is Eq to c
You can try all sorts of permutation here and you will see a is Eq to c.
Base case n==1 => true because of Symmetry.