Starting from October 2015 ratings formulas are open. They are given in the post. It is likely that from time to time we will change them slightly, it will be reflected here.
The basic idea of Codeforces rating system is to generalize Elo rating to support games with multiple participants.
Each community member is characterized by value ri — integer number. Roughly speaking, the higher value means better results in the contests. Rating is calculated/recalculated so that the equality strives to be correct:
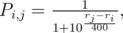
where Pi, j is probability that the i-th participant has better result than the j-th participant. Therefore for two participants the probability to win/lose depends on subtraction of their ratings. For example, if the difference of ratings is equal to 200 then stronger participant will win with probability ~0.75. If the difference of ratings is equal to 400 then stronger participant will win with probability ~0.9.
After a contest the values ri change in a way to satisfy main formula better.
Let’s calculate expected place seedi for each participant before contest. It equals to the sum over all other participants of probabilities to win (to have better place than) the i-th plus one because of 1-based place indices:
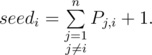
For example, before Codeforces Round 318 [RussianCodeCup Thanks-Round] (Div. 1) tourist had rating 3503 and his seed was ~1.7, and Petr had rating 3029 and expected place ~10.7.
General idea is to increase ri if actual place is better than seedi and to decrease ri if actual place is worse than seedi.
Having seedi and actual place, let’s calculate their geometric mean mi. You can think about it as an something average between seedi and actual place shifted to the better place. Using binary search find such rating value R which the i-th participant should have to have a seedi = mi. Obviously the rating ri should be modified to become closer to R. We use di = (R - ri) / 2 as rating change for the i-th participant.
It's almost all except the phase of fighting against inflation. Inflation works as follows: the rich get richer. We will try to avoid it. If we assume that the rating was already calculated fair (i.e. everybody has perfect statistically based rating) then expected change of rating after a contest is equal to zero for any participant.
Choose a group of the most rated (before the round) participants and decide that their total rating shouldn’t change. We use heuristic value 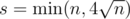 as a size of such group. Let’s find the sum of di over participants from group and adjust all values di (for all participants) to make the sum to be zero. In other words, ri = ri + inc, where inc = - sums / s, sums is sum of di over s participants from chosen group.
as a size of such group. Let’s find the sum of di over participants from group and adjust all values di (for all participants) to make the sum to be zero. In other words, ri = ri + inc, where inc = - sums / s, sums is sum of di over s participants from chosen group.
After the round 327 we restricted the effect in following way. Firstly, we do ri = ri + inc, where inc = - sum(di) / n - 1, sum(di) is sum of all di. It makes the sum of all di to be near zero and non-positive in the same time. Secondly, we apply idea from the previous paragraph, but inc = min(max( - sums / s, - 10), 0). Thus, the effect of modification can not reduce rating for more than ~10 points.
By the way, for any consistent rating the following assertions should be true:
- if the participant A had worse rating than the participant B before the contest and finished the contest on the worse place then after recalculations the the rating of A can’t be greater than the rating of B
- if A finished the contest better than B but A had worse rating before the contest then A should have equal or greater rating change than B.
In particular, formulas are tested to satisfy the both items on each ratings recalculation.
You may read the actual Codeforces code to recalculate ratings here: 13861109.











It would be nice if contestants can see their expected place in the standings or somewhere else for a particular round.
"General idea is to increase ri if actual place is better than seedi and to decrease ri if actual place is worse than seedi. "
It would be really cool if we know seedi before. We will know the maximum rank required to have an increase in our rating.
But the problem is seedi can only be calculated when we know who all the actual participants beforehand. Which is not possible because many registrants do not actually participate in the live contest.
One solution can be to do the calculations in the live contest and update seedi for each participant after a fixed interval of time (say 10 minutes and if new participants get added). 😀😃
Would be awesome to have a expected rank on dashboard while we solve problems in the live contest. Can't imagine the adrenaline rush :P
At least showing the expected rank after a contest is still possible.
Yeah that should be a nice feature.
Good ideas. But I don't think Codeforces will ever do any of this. I think they should also assume all registrants participated in the round even if they didn't submit any solutions. That way, the number of registrants would be the real number of people who had a chance to participate. Every round a lot of people register and then never show up during the contest.
I m sorry, but considering all the registered participants, and then performing the rating changes, assuming no change for those who didn
t participate doesnt satisfy the Basic Maths :PCould you please translate this blog to English so that non-Russian people can read it, since this is important blog and no one should miss it
Auto comment: topic has been translated by MikeMirzayanov(original revision, translated revision, compare)
Very informative. Thanks for making it open.
Wow, geometric mean. That explains why it's easier to go up than down.
Anyway thanks for making it open; community discussion can only help! I might have more detailed thoughts later.
My thoughts parallel those of JohStraat below, though perhaps changing geometric to arithmetic mean is a bit of an overcorrection in terms of punishing bad performances. It seems to me the current rating system is a collection of hacks on Elo, designed to have some desired effect. It works fairly well but has some strange properties: for instance, if the number of contestants changed drastically, the relative meaning of geometric mean would change.
I would rather instead we build a rigorous statistical model. For example, how about we suppose a person's rating r is drawn from a distribution centered at their "true skill" s with variance σ12. Their performance p in a specific contest is drawn from a distribution centered at s with variance σ22. Player i beats Player j iff pi > pj. Now we should perform a Bayes update, changing each player's rating to the mean of their posterior marginal distribution for s (the prior has s independently drawn for each player from logistic(r, σ12)).
Technical issues: the Bayes update may require numerical integration. I believe many of the partial sums can be precomputed and shared, so it should be fast enough. In a basic implementation, σ1 and σ2 should be global constants. If we want to get fancier, σ2 can be a function of certain factors that affect how accurately the contest measures skill; for instance, it makes sense to have σ2 be inversely proportional to the square root of the contest length. σ2 might also be higher for contestants who are much too strong or too weak for a given contest's difficulty. σ1 can be a property of each contestant, subject to Bayes update jointly with r: normally each contest will decrease the uncertainty, so we should also increment σ12 by a constant amount to account for the fact that people's skills change. Giving unrated coders a very high σ1 also prevents them from giving or draining too many points from the system for inflation or deflation.
I don't know how feasible it is, but it would be nice to invent a formula that naturally preserves some invariant such as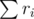 (or maybe something involving the $\sigma_1$s), as normal Elo does...
(or maybe something involving the $\sigma_1$s), as normal Elo does...
+1 This is very similar to the Glicko rating system used by many online chess sites.
Right, when σ1, σ2 are allowed to vary, my idea is essentially based on Glicko. When they are constant, it's closer to Elo but with a few distinctions:
1) A contestant's rank should not be treated as a sum of independent pairwise matchups. Instead, each pi is drawn independently.
2) pi is drawn from a logistic centered at si, whose prior is in turn logistic centered at ri.
These should be sufficient to prevent unduly punishing a single bad round, without resorting to the geometric mean. After all, it's much less surprising to get one bad draw from a logistic distribution, than 100 bad draws from independent normals. And if it's still not enough, we can consider asymmetric distributions for pi and si. Now it remains to derive some fast-computable formulas...
Ok I wrote up a draft! I plan to write more in the future, but for now just assume σ1 < σ2 and they are global constants.
https://github.com/EbTech/EloR
I conjecture that this system will have better properties than previous ranking-based update algorithms such as currently used by CF and TC.
Thanks for the clear explanation! Is it possible to open source the rating system? Put the code on Github? That way people can build tools on top of it? Maybe even parts of Codeforces (e.g. test evaluator etc) can be open sourced? Thanks again!
Please explain it easily. I don't understand.
you can understood the whole concept from here..
https://en.wikipedia.org/wiki/Glicko_rating_system
What is the actual time taken to do all the calculations say for 5000 participants.
I didn't get the inflation "The rich get richer" case. How is it a problem ?
Yes, that isn't even inflation, it is inequality which isn't a problem in contests. The problem is if 400 rating difference doesn't signify a 10 to 1 win-loss ratio. Mike said that Tourist had an expected position of 1.7, but if you look at his history it isn't even close to that:
http://codeforces.com/contests/with/tourist
Sure he wins often, but he isn't even close to averaging a rank of 1.7 even before the blunder. And that blunder which is statistically impossible given his rating just lost him as much rating as he would get from winning 2 competitions. So he would have an expected rank of 1.7 if he just continued to alternate getting rank 1 twice and rank 168 once which doesn't really add up. Actual elo is made in such a way that it should be all but impossible to reach ratings as high as 3500, such ratings signify that there is a problem with how the rating is calculated.
Then in Codeforces Round #328 (Div. 2),There is a problem: Give you the rules of the rating changing and all participants' standings with their ratings; Calculate the change of ratings.
This causes inflation! I was wondering why people lost so extremely little rating for coming last in a contest, but now it is clear! With this system a person who places totally randomly will according to the system be expected to beat roughly 56% of contestants. So why not just do this instead:
This way sum of expected rank and actual rank will be the same. Sure it might punish people with high rating when they screw up, but protection of people with high rating is what causes rating inflation in the first place!
Difference between 1st and 10th place is much larger than between 41st and 50th.
That kind of reasoning is why 400 rating isn't even close to the alleged 10 to 1 chance of beating someone at the top. The point about ELO is that it is exponential so getting 2800 rating in chess means that you are an historical figure while 2700 is achieved by quite a lot of people. If codeforces used a real ELO then we would have such walls as well.
So with my system the difference between rank 1 and 10 is that rank 10 will never let you reach legendary status while rank 1 can, while the difference between rank 40 and 50 gets lost in the crowds.
As an example someone who alternates between rank 1 and 3 is obviously equal to someone who gets rank 2 every time (just take two people alternating and one stable and each of them beats each other 50% of the time) but this system glorifies the person with inconsistent results.
I think that one thing explaining why top scores on CF are higher than 2800 and that ratings functions are changing much more than in chess is that in chess one game is one win or one loss and on CF one round is like 600 games with particular users. In CF lack of one "ll" can cause your rating go down by 100 instead of having +50, it shouldn't be the difference between legendary user and "just red".
Btw I don't agree with your last paragraph. It depends on what is a measure you're using. If you take percentage of wins then you're right, however I don't think that is a perfect measure (in my opinion even pretty far from one). As I said, climbing on top of standings is much harder than on its lower parts. Assume that I did AB problems on one round and that gives me 100th place. If I solve problem C I will advance to 20th place. If I solve C and D I will advance to 1st position. Take 5 such rounds. Do you think that solving 4xABCD + 1xAB should be equivalent to 5xABC. Given your measure, it will be.
I probably don't get something in the math — how is this related?
Me too.
"We use di = (R - ri) / 2 as rating change for the i-th participant." initially it was di = (R-ri) / 3 and now this is di = (R-ri) / 2. was that a typo or the formula has been modified ?
"Let’s calculate expected place seedi for each participant before contest. It equals to the sum over all other participants of probabilities to win (to have better place than) the i-th plus one because of 1-based place indices:
Where is "plus one" in the formula of seed? Was that a typo?
I don't see there is a problem with the rating inflation if the skill level of existing members do increase overtime (relative to newcomers to Codeforces).
I think once you put in custom formulas / adjustments / caps, the basic principle "If the difference of ratings is equal to 400 then stronger participant will win with probability ~0.9." is not true anymore. Can any one correct me?
"Choose a group of the most rated (before the round) participants and decide that their total rating shouldn’t change. " is extremely flawed... are you expecting those who put hard work and training will not become better over time? (especially over the mediocre ones?)
Rating should be relative to not absolute. If because of some magic spell, all users become two times better than they were, keeping rating without changes is only sane solution. Moreover I guess it is a reasonable assumption that average level of cf member is almost constant function in time.
It isn't since competitive programming is still in an infant stage compared to most competitions. I mean, the world record in most physical sports 50 years ago barely qualifies you compete at the international level today and at least I think that refinements of training/techniques would have much less impact on lets say running than on competitive programming.
What happened to the cap of rating fall at ~-110 ;__;? Since my performances have big variances, that was really important to me xD. I have never experienced such a big fall or even similar one in Div1-only contest as yesterday's -140 ._. (even though I had greater fails)
Ho Lee Fuk Wi Tu Lo https://www.youtube.com/watch?v=17GbGmDORwk
He does not have two colors!
It seems that tourist's rating diverges. Is it reasonable?
Does this mean that it is easier to go up than go down in rating? Though I was confused about how to calculate this by myself.
I have a question about the changes. Why the history of color changes is not preserved? Initially red color was granted for getting 2000 rating. I understand the changes of colors and ranks but they should not affect the past.
Could you please reflect old color status on participants profiles?
Edit. Perhaps a better place for this, would be post which announces the changes, however there were 2 changes already and that post was mentioned recently, so I used it as a place to express my thoughts.
Last time there was a poll and most of participants didn't care about history preserving
Ok, I found it here: http://codeforces.com/blog/entry/20629
Well — let it be then...
Edit. Even though the voting rules were obviously in favor of the first option — those who were red at that time had a much bigger voting power and obviously it was more attractive for them to prevent others from ever achieving a red color.
So performance rating is roughly equal to Oldrating + change * 4?
Can anybody explain to me that how does this rating system remain consistent? I couldn't find any theoretical explanation toward consistency of this rating system.
Somewhere I saw ready-made formulas on how to get rid of the binary search when calculating the expected place $$$R$$$. Can you help me find it?
are you referring to this (under ELO system and expected rank): link ?
No, in my post above I mentioned that we use a binary search to find $$$R$$$. But it can be replaced with explicit calculations, and I previously saw a comment with such formulas. In the post you mentioned I don't see such formulas.
Let $$$n$$$ be the no of participants in a contest. $$$n$$$ is typically 20k-40k, but the rating range is [-500,4500], let $$$R = 5000$$$,
The current algorithm calculates everyone's rating in $$$O(n*n*logR)$$$
The rating calculation can be done in $$$O(n*R)$$$, for 35-70x speedup.Update 1: The rating calculation can be done in $$$O(R*R+n*logR)$$$, for 140-550x speedup.
Instead of running this loop in $$$O(n*n)$$$, we can run it in $$$(R*R)$$$ by maintaining the frequency of each rating point and calculating the seed for each rating. One can also overkill by using FFT in $$$O(R*logR)$$$
This one takes $$$O(n*n*logR)$$$ and can be optimised to run in $$$O(n*R+n*logR)$$$, with precalculations.This one takes $$$O(n*n*logR)$$$ and can be optimised to run in $$$O(R*R+n*logR)$$$, with precalculations.Precalculation -
if (getSeed(contestants, mid) < rank) { right = mid; } else { left = mid; }We can precalculate ranks for each rating point in the range [low,high] in $$$O(n*R)$$$We can precalculate ranks for each rating point in the range [low,high] in $$$O(R*R)$$$, by first calculating frequency of each rating point, and then running two for loops in O(R*R).
So that
getRatingToRank(contestants, midRank)will run in $$$O(logR)$$$ instead of current $$$O(n*logR)$$$Once this is done, the main for loop of
needRatingwill run in $$$O(n*logR+R*R)$$$ instead of the current $$$O(n*n*logR)$$$validateDeltas(contestants);It's too risky to touch, although we can use some 2D range query data structures to make it subquadratic.can some one suggest me how to calculate leetcode rating accurately and how can i convert it to codeforces equvivalent(i meant may be a guardian maybe map to 1700 etc...) its needed for my project.
For Chinese users, I'd like to giv u a link to a blog which was written by rui_er in Chinese about how to calc the rating.
Blog