Aim — To multiply 2 n-degree polynomials in 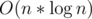 instead of the trivial O(n2)
instead of the trivial O(n2)
I have poked around a lot of resources to understand FFT (fast fourier transform), but the math behind it would intimidate me and I would never really try to learn it. Finally last week I learned it from some pdfs and CLRS by building up an intuition of what is actually happening in the algorithm. Using this article I intend to clarify the concept to myself and bring all that I read under one article which would be simple to understand and help others struggling with fft.
Let’s get started 
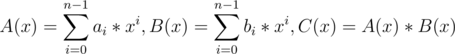
Here A(x) and B(x) are polynomials of degree n - 1. Now we want to retrieve C(x) in 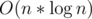
So our methodology would be this 
- Convert A(x) and B(x) from coefficient form to point value form. (FFT)
- Now do the O(n) convolution in point value form to obtain C(x) in point value form, i.e. basically C(x) = A(x) * B(x) in point value form.
- Now convert C(x) from point value from to coefficient form (Inverse FFT).
Q) What is point value form ?
Ans) Well, a polynomial A(x) of degree n can be represented in its point value form like this  A(x) = {(x0, y0), (x1, y1), (x2, y2), ..., (xn - 1, yn - 1)} , where yk = A(xk) and all the xk are distinct.
A(x) = {(x0, y0), (x1, y1), (x2, y2), ..., (xn - 1, yn - 1)} , where yk = A(xk) and all the xk are distinct.
So basically the first element of the pair is the value of x for which we computed the function and second value in the pair is the value which is computed i.e A(xk).
Also the point value form and coefficient form have a mapping i.e. for each point value form there is exactly one coefficient representation, if for k degree polynomial, k + 1 point value forms have been used at least.
Reason is simple, the point value form has n variables i.e, a0, a1, ..., an - 1 and n equations i.e. y0 = A(x0), y1 = A(x1), ..., yn - 1 = A(xn - 1) so only one solution is there.
Now using matrix multiplication the conversion from coefficient form to point value form for the polynomial 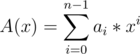 can be shown like this
can be shown like this 
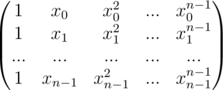
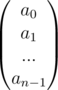
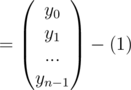
And the inverse, that is the conversion from point value form to coefficient form for the same polynomial can be shown as this 
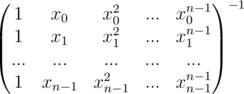
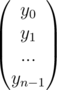
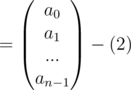
Now, let's assume A(x) = x2 + x + 1 = {(1, 3), (2, 7), (3, 13)} and B(x) = x2 - 3 = {(1, - 2), (2, 1), (3, 6)}, where degree of A(x) and B(x) = 2
Now as C(x) = A(x) * B(x) = x4 + x3 - 2x2 - 3x - 3
C(1) = A(1) * B(1) = 3 * - 2 = - 6, C(2) = A(2) * B(2) = 7 * 1 = 7, C(3) = A(3) * B(3) = 13 * 6 = 78
So C(x) = {(1, - 6), (2, 7), (3, 78)} where degree of C(x) = degree of A(x) + degree of B(x) = 4
But we know that a polynomial of degree n - 1 requires n point value pairs, so 3 pairs of C(x) are not sufficient for determining C(x) uniquely as it is a polynomial of degree 4.
Therefore we need to calculate A(x) and B(x), for 2n point value pairs instead of n point value pairs so that C(x)’s point value form contains 2n pairs which would be sufficient to uniquely determine C(x) which would have a degree of 2(n - 1).
Now if we had performed this algorithm naively it would have gone on like this 
Note — This is NOT the actual FFT algorithm but I would say that understanding this would layout framework to the real thing.
Note — This is actually DFT algorithm, ie. Discrete fourier transform.
- We construct the point value form of A(x) and B(x) using x0, x1, ..., x2n - 1 which can be made using random distinct integers. So point value form of A(x) = {(x0, α0), (x1, α1), (x2, α2), ..., (x2n - 1, α2n - 1)} and B(x) = {(x0, β0), (x1, β1), (x2, β2), ..., (x2n - 1, β2n - 1)} - (1) Note — The x0, x1, ..., x2n - 1 should be same for A(x) and B(x). This conversion takes O(n2).
- As C(x) = A(x) * B(x), then what would have been the point-value form of C(x) ?
If we plug in x0 to all 3 equations then we see that
C(x0) = A(x0) * B(x0)
C(x0) = α0 * β0
So C(x) in point value form will be C(x) = {(x0, α0 * β0), (x1, α1 * β1), (x2, α2 * β2), ..., (x2n - 1, α2n - 1 * β2n - 1)}
This is the convolution, and it’s time complexity is O(n) - Now converting C(x) back from point value form to coefficient form can be represented by using the equation 2. Here calculating the inverse of the matrix requires LU decomposition or Lagrange’s Formula. I won’t be going into depth on how to do the inverse, as this wont be required in the REAL FFT. But we get to understand that using Lagrange’s Formula we would’ve been able to do this step in O(n2).
Note — Here the algorithm was performed wherein we used x0, x1, ..., x2n - 1 as ordinary real numbers, the FFT on the other hand uses roots of unity instead and we are able to optimize the O(n2) conversions from coefficient to point value form and vice versa to 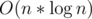 because of the special mathematical properties of roots of unity which allows us to use the divide and conquer approach. I would recommend to stop here and re-read the article till here until the algorithm is crystal clear as this is the raw concept of FFT.
because of the special mathematical properties of roots of unity which allows us to use the divide and conquer approach. I would recommend to stop here and re-read the article till here until the algorithm is crystal clear as this is the raw concept of FFT.
A math primer on complex numbers and roots of unity would be a must now.
Q) What is a complex number ?
Answer — Quoting Wikipedia, “A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, that satisfies the equation i2 = - 1. In this expression, a is the real part and b is the imaginary part of the complex number.” The argument of a complex number is equal to the magnitude of the vector from origin (0, 0) to (a, b), therefore arg(z) = a2 + b2 where z = a + bi.
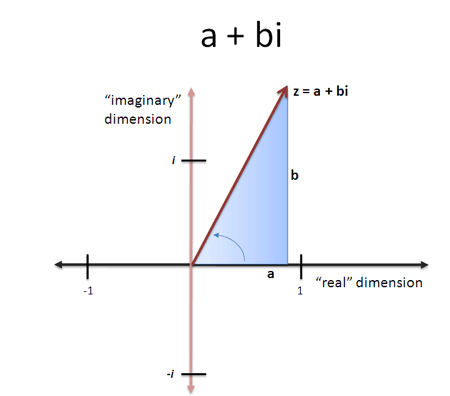
Q) What are the roots of unity ?
Answer — An nth root of unity, where n is a positive integer (i.e. n = 1, 2, 3, ...), is a number z satisfying the equation zn = 1. 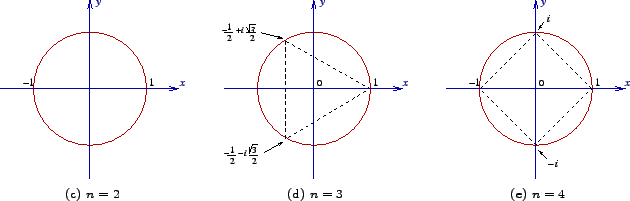
In the image above, n = 2, n = 3, n = 4, from LEFT to RIGHT.
Intuitively, we can see that the nth root of unity lies on the circle of radius 1 unit (as its argument is equal to 1) and they are symmetrically placed ie. they are the vertices of a n — sided regular polygon.
The n complex nth roots of unity can be represented as e2πik / n for k = 0, 1, ..., n - 1
Also 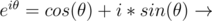 Graphically see the roots of unity in a circle then this is quite intuitive.
Graphically see the roots of unity in a circle then this is quite intuitive.
If n = 4, then the 4 roots of unity would’ve been e2πi * 0 / n, e2πi * 1 / n, e2πi * 2 / n, e2πi * 3 / n = (e2πi / n)0, (e2πi / n)1, (e2πi / n / )2, (e2πi / n)3 where n should be substituted by 4.
Now we notice that all the roots are actually power of e2πi / n. So we can now represent the n complex nth roots of unity by wn0, wn1, wn2, ..., wnn - 1, where wn = e2πi / n
Now let us prove some lemmas before proceeding further 
Note — Please try to prove these lemmas yourself before you look up at the solution :)
Lemma 1 — For any integer n ≥ 0, k ≥ 0 and d ≥ 0, wdndk = wnk
Proof — wdndk = (e2πi / dn)dk = (e2πi / n)k = wnk
Lemma 2 — For any even integer n > 0, wnn / 2 = w2 = - 1
Proof — wnn / 2 = w2 * (n / 2)n / 2 = wd * 2d * 1 where d = n / 2
wd * 2d * 1 = w21 — (Using Lemma 1)
w21 = eiπ = cos(π) + i * sin(π) = - 1 + 0 = - 1
Lemma 3 — If n > 0 is even, then the squares of the n complex nth roots of unity are the (n/2) complex (n/2)th roots of unity, formally (wnk)2 = (wnk + n / 2)2 = wn / 2k
Proof — By using lemma 1 we have (wnk)2 = w2 * (n / 2)2k = wn / 2k, for any non-negative integer k. Note that if we square all the complex nth roots of unity, then we obtain each (n/2)th root of unity exactly twice since,
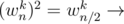 (Proved above)
(Proved above)
Also, (wnk + n / 2)2 = wn2k + n = e2πi * k' / n, where k' = 2k + n
e2πi * k' / n = e2πi * (2k + n) / n = e2πi * (2k / n + 1) = e(2πi * 2k / n) + (2πi) = e2πi * 2k / n * e2πi = wn2k * (cos(2π) + i * sin(2π))
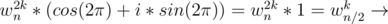 (Proved above)
(Proved above)
Therefore, (wnk)2 = (wnk + n / 2)2 = wn / 2k
Lemma 4 — For any integer n ≥ 0, k ≥ 0, wnk + n / 2 = - wnk
Proof — wnk + n / 2 = e2πi * (k + n / 2) / n = e2πi * (k / n + 1 / 2) = e(2πi * k / n) + (πi) = e2πi * k / n * eπi = wnk * (cos(π) + i * sin(π)) = wnk * ( - 1) = - wnk
1. The FFT — Converting from coefficient form to point value form
Note — Let us assume that we have to multiply 2 n — degree polynomials, when n is a power of 2. If n is not a power of 2, then make it a power of 2 by padding the polynomial's higher degree coefficients with zeroes.
Now we will see how is A(x) converted from coefficient form to point value form in 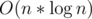 using the special properties of n complex nth roots of unity.
using the special properties of n complex nth roots of unity.
yk = A(xk)
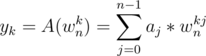
Let us define 
Aeven(x) = a0 + a2 * x + a4 * x2 + ... + an - 2 * xn / 2 - 1, Aodd(x) = a1 + a3 * x + a5 * x2 + ... + an - 1 * xn / 2 - 1
Here, Aeven(x) contains all even-indexed coefficients of A(x) and Aodd(x) contains all odd-indexed coefficients of A(x).
It follows that A(x) = Aeven(x2) + x * Aodd(x2)
So now the problem of evaluating A(x) at the n complex nth roots of unity, ie. at wn0, wn1, ..., wnn - 1 reduces to 
- Evaluating the n/2 degree polynomials Aeven(x2) and Aodd(x2). As A(x) requires wn0, wn1, ..., wnn - 1 as the points on which the function is evaluated.
Therefore A(x2) would’ve required (wn0)2, (wn1)2, ..., (wnn - 1)2.
Extending this logic to Aeven(x2) and Aodd(x2) we can say that the Aeven(x2) and Aodd(x2) would require (wn0)2, (wn1)2, ..., (wnn / 2 - 1)2 ≡ wn / 20, wn / 21, ..., wn / 2n / 2 - 1 as the points on which they should be evaluated.
Here we can clearly see that evaluating Aeven(x2) and Aodd(x2) at wn / 20, wn / 21, ..., wn / 2n / 2 - 1 is recursively solving the exact same form as that of the original problem, i.e. evaluating A(x) at wn0, wn1, ..., wnn - 1. (The division part in the divide and conquer algorithm)
- Combining these results using the equation A(x) = Aeven(x2) + x * Aodd(x2). (The conquer part in the divide and conquer algorithm).
Now, A(wnk) = Aeven(wn2k) + wnk * Aodd(wn2k), if k < n / 2, quite straightforward
And if k ≥ n / 2, then A(wnk) = Aeven(wn / 2k - n / 2) - wnk - n / 2 * Aodd(wn / 2k - n / 2)
Proof — A(wnk) = Aeven(wn2k) + wnk * Aodd(wn2k) = Aeven(wn / 2k) + wnk * Aodd(wn / 2k) using (wnk)2 = wn / 2k
A(wnk) = Aeven(wn / 2k) - wnk - n / 2 * Aodd(wn / 2k) using wnk' + n / 2 = - wnk' i.e. (Lemma 4), where k' = k - n / 2.
So the pseudocode (Taken from CLRS) for FFT would be like this 
1.RECURSIVE-FFT(a)
2. n = a.length()
3. If n = = 1 then return a //Base Case
4. wn = e2πi / n
5. w = 1
6. aeven = (a0, a2, ..., an - 2)
7. aodd = (a1, a3, ..., an - 1)
8. yeven = RECURSIVE - FFT(aeven)
9. yodd = RECURSIVE - FFT(aodd)
10. For k = 0 to n / 2 - 1
11. yk = ykeven + w * ykodd
12. yk + n / 2 = ykeven - w * ykodd
13. w * = wn
14. return y;
2. The Multiplication OR Convolution
This is simply this 
1.a = RECURSIVE-FFT(a), b = RECURSIVE-FFT(b) //Doing the fft.
2.For k = 0 to n - 1
3. c(k) = a(k) * b(k) //Doing the convolution in O(n)
3. The Inverse FFT
Now we have to recover c(x) from point value form to coefficient form and we are done. Well, here I am back after like 8 months, sorry for the trouble. So the whole FFT process can be show like the matrix 
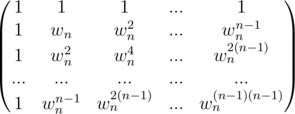

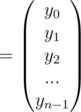
The square matrix on the left is the Vandermonde Matrix (Vn), where the (k, j) entry of Vn is wnkj
Now for finding the inverse we can write the above equation as 
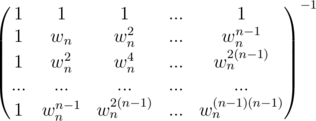

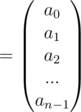
Now if we can find Vn - 1 and figure out the symmetry in it like in case of FFT which enables us to solve it in NlogN then we can pretty much do the inverse FFT like the FFT. Given below are Lemma 5 and Lemma 6, where in Lemma 6 shows what Vn - 1 is by using Lemma 5 as a result.
Lemma 5 — For n ≥ 1 and nonzero integer k not a multiple of n, 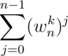 = 0
= 0
Proof — 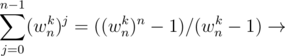 Sum of a G.P of n terms.
Sum of a G.P of n terms.
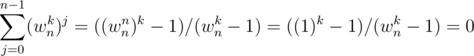
We required that k is not a multiple of n because wnk = 1 only when k is a multiple of n, so to ensure that the denominator is not 0 we required this constraint.
Lemma 6 — For j, k = 0, 1, ..., n - 1, the (j, k) entry of Vn - 1 is wn - kj / n
Proof — We show that Vn - 1 * Vn = In, the n * n identity matrix. Consider the (j, j') entry of Vn - 1 * Vn and let it be denoted by [Vn - 1 * Vn]jj'
So now 
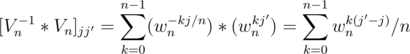
Now if j' = j then wnk(j' - j) = wn0 = 1 so the summation becomes 1, otherwise it is 0 in accordance with Lemma 5 given above. Note here that the constraints fore Lemma 5 are satisfied here as n ≥ 1 and j' - j cannot be a multiple of n as j' ≠ j in this case and the maximum and minimum possible value of j' - j is (n - 1) and - (n - 1) respectively.
So now we have it proven that the (j, k) entry of Vn - 1 is wn - kj / n.
Therefore, 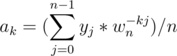
The above equation is similar to the FFT equation 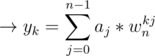
The only differences are that a and y are swapped, we have replaced wn by wn - 1 and divided each element of the result by n
Therefore as rightly said by Adamant that for inverse FFT instead of the roots we use the conjugate of the roots and divide the results by n.
That is it folks. The inverse FFT might seem a bit hazy in terms of its implementation but it is just similar to the actual FFT with those slight changes and I have shown as to how we come up with those slight changes. In near future I would be writing a follow up article covering the implementation and problems related to FFT.
References used — Introduction to Algorithms(By CLRS) and Wikipedia
Feedback would be appreciated. Also please notify in the comments about any typos and formatting errors :)











How can you do a CONVULSION using FFT?
Sorry it is a typo, thanks for pointing out.
Auto comment: topic has been updated by sidhant (previous revision, new revision, compare).
This is gold to me, I finally start to understand how FFT works. I'm looking forward to the 3rd part!
Another great resource : http://www.cs.cmu.edu/afs/cs/academic/class/15451-s10/www/lectures/lect0423.txt
Finally, a topic on FFT that a high school student can understand. Very useful topic, thank you a lot!
Hi xuanquang1999 what topics do you need to understand fft?
I'm not sure if I understand your question correctly, but I meant this topic (the one that you're commenting on).
Mmm I think I was not clear enough, My question is that if you need to know some topics (math's, computer science's or some algorithms) before studying FFT?
polynomials, matrices, complex numbers
Great tutorial! :D
Thanks! :D
Finally an understandable tutorial on FFT!
Auto comment: topic has been updated by sidhant (previous revision, new revision, compare).
Example of DFT elaborated.
Waiting for inverse FFT.
Coming in a week!
Still waiting :)
still waiting dogo
Sorry I was a bit busy the past few months, would be finishing off this article within next week!!
Such busy dogo much wow!
This is his real account NibNalin
Spoiler: use FFT with conjugation to root instead of root itself. And divide values by n after this.
Nice tutorial xD
Just two observations:
1) When you explain the roots of unity and give the example of n=4, you wrote that e2π i * 0 / n = e1, whereas it should be e0
2) In the proof of lemma 3, you used twice the expression (cos(2) + i * sin(2)), instead of (cos(2π) + i * sin(2π))
Thanks for pointing out, will fix it :)
Any questions on codeforces using this concept?
Is that a typo?
C(x) = {(1, 6), (2, 7), (3, 78)} should be C(x) = {(1, -6), (2, 7), (3, 78)}???
Thanks for pointing out, fixed :)
Auto comment: topic has been updated by sidhant (previous revision, new revision, compare).
Please do post Implementation and problems too! BTW Awesome Tutorial (y).
nice editorial
"for each point value form there is exactly one coefficient representation and vice — versa". Above statement is not true, for each coefficient representation there may be many point value form, point value form is not unique for a polynomial, you can choose any N point to uniquely identify a n-bounded polynomial.
Yes, my bad. I fill fix it.
Auto comment: topic has been updated by sidhant (previous revision, new revision, compare).
Auto comment: topic has been updated by sidhant (previous revision, new revision, compare).
good job sidhant!
Russian speaking contestants use e-maxx. Very comprehensive explanation with codes. As bonus you get optimization tricks + references to base problems.
Nice tutorial.
I think, there is a typo here: Q) What is point value form ? Ans) Well, a polynomial A(x) of degree n can be represented in its point value form like this
Degree of A(x) should be n-1.
Auto comment: topic has been updated by sidhant (previous revision, new revision, compare).
is really a good TV drama, I mean season 1, season 2 confused me
is it possible in fft.. all possible x^y minimum value...
like , A = a1x^3 + b1x^2+ c1x + d1 B = a2x^3 + b2x^2+ c2x + d1 now possible possible way to create x^3= (a1*d1),(b1*c2),(c1*b2),(d1*a2) now i want min((a1*d1),(b1*c2),(c1*b2),(d1*a2))
if any other algorithm what is it?
Hi sidhant! I would just like to point that you mixed a concept in the article! Where you said "The argument of a complex number is equal to the magnitude of the vector from origin" you are actually talking of the modulus of the complex number, not its argument. Aside from that, excellent article! EDIT: and the modulus is actually the square root of both terms squared, I think you forgot the square root.
problems on FFT?
Here.
thanks :D
a̶r̶g̶u̶m̶e̶n̶t̶ modulus. argument is the angle.
This is a great source to learn fft — http://web.cecs.pdx.edu/~maier/cs584/Lectures/lect07b-11-MG.pdf
In lemma 6 there was a typo that confused me a bit. I know this blog post is 4 years old but the fist summation on line 2 of lemma 6 has the /n in the wrong place. The first term in the summation should be (1/n) * w_n^(-kj), not w_n^(-kj/n). Either way, great blog! Time to see how this stuff is impled.
it should look like $$$\frac{w_n^{-kj}}{n}$$$ or $$$\frac{1}{n}\cdot w_n^{-kj}$$$
An excellent complimentary video https://www.youtube.com/watch?v=h7apO7q16V0
I have started learning FFT a few days ago.
Suppose, I have a vector <.Complex> A.
Will anyone please tell me
1.What does FFT(A) really mean?
2.What is the physical meaning of it?
sidhant I don't see this anymore it says Unable to parse markup [type=CF_MARKDOWN]
https://codeforces.cc/topic/43659/en14
This is the last viewable version I can find!
-QuangBui(YT/CP)
This tutorial is too good to exist.
Can someone please tell me, in the conquer part, why A(Wn ^k) is different for k<n/2 and k>=n/2?
Why do you need to divide by n for the roots of the inverse matrix? Doesn't it also work without the division by n? Can someone explain please? (I mean that I 'think' the sum from lemma 6 is true without the /n...)
Nvm, I took a closer look and I understood..Sorry for spam
checkout this video for hindi explanation: https://www.youtube.com/watch?v=tXpzsSLxx3Q