You should know only one fact to solve this task: 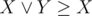 . This fact can be proved by the truth table. Let's use this fact:
. This fact can be proved by the truth table. Let's use this fact:  . Also
. Also 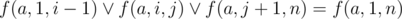 . According two previous formulas we can get that f(a, 1, n) ≥ f(a, i, j). Finally we can get the answer. It's equal to f(a, 1, N) + f(b, 1, N).
. According two previous formulas we can get that f(a, 1, n) ≥ f(a, i, j). Finally we can get the answer. It's equal to f(a, 1, N) + f(b, 1, N).
Time: 
Memory: 
Let's define timeRi as a number of last query, wich repaint row with number i, timeCj – as number of last query, wich repaint column with number j. The value in cell (i, j) is equal amax(timeRi, timeCj).
Time: 
Memory: 
If we have some pair of queries that ri ≥ rj, i > j, then we can skip query with number j. Let's skip such queries. After that we get an array of sorted queries (ri ≤ rj, i > j). Let's sort subarray a1..max(ri) and copy it to b. For proccessing query with number i we should record to ari - 1..ri first or last(it depends on ti - 1) ri - 1 - ri + 1 elementes of b. After that this elements should be extract from b. You should remember that you need to sort subarray a1..rn, after last query.
Time: 
Memeory: 
Let's define S[i] as i - th block of S, T[i] — as i - th block of T.Also S[l..r] = S[l]S[l + 1]...S[r] and T[l..r] = T[l]T[l + 1]...T[r].
T is substring of S, if S[l + 1..r - 1] = T[2..m - 1] and S[l].l = T[1].l and S[l].c ≥ T[1].c and S[r].l = T[m].l and S[r].c ≥ T[m].c. Let's find all matches of T[l + 1..r - 1] in S and chose from this matches, witch is equal T.You can do this by Knuth–Morris–Pratt algorithm.
This task has a some tricky test cases:
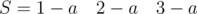 and
and 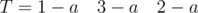 . Letters in the adjacent blocks are may be same.This problem can be solved by the union of adjacent blocks with same letter.
. Letters in the adjacent blocks are may be same.This problem can be solved by the union of adjacent blocks with same letter. and
and 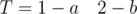 . Count of T blocks are less than 3. Such cases can be proccess singly.
. Count of T blocks are less than 3. Such cases can be proccess singly.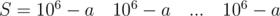 and
and 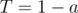 . Answer for this test should be stored at long long.
. Answer for this test should be stored at long long.
Time: 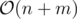
Memory: 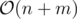
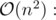
The operation, which has been described in the statement, is cyclic shift of some subarray. Let's try to solve this problem separately for left cyclic shift and for right cyclic shift. Let's define 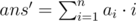 as answer before(or without) cyclic shift, Δans = ans - ans' — difference between answer after cyclic shift and before. This difference can be found by next formulas:
as answer before(or without) cyclic shift, Δans = ans - ans' — difference between answer after cyclic shift and before. This difference can be found by next formulas:
For left cyclic shift:
Δl, r = (al·r + al + 1·l + ... + ar·(r - 1)) - (al·l + al + 1·(l + 1) + ... + ar·r) = al·(r - l) - (al + 1 + al + 2 + ... + ar)
For right cyclic shift:
Δ'l, r = (al·(l + 1) + al + 1·(l + 2) + ... + ar·l) + (al·l + al + 1·(l + 1) + ... + ar·r) = (al + al + 1 + ... + ar - 1) + ar·(l - r)
You can find this values with complexity 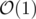 , using prefix sums,
, using prefix sums, 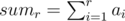 .
.
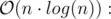
Let's try to rewrite previous formulas:
For left cyclic shift: Δl, r = (al·r - sumr) + (suml - al·l)
For right cyclic shift: Δ'l, r = (ar·l - suml - 1) + (sumr - 1 - ar·r)
You can see, that if you fix l for left shift and r for right shift, you can solve this problem with complexity 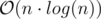 using Convex Hull Trick.
using Convex Hull Trick.
Time: 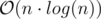
Memory: 










Im failing to understand one thing....jst changed long lont int to int....was getting tle during the contest...now got an AC...my earlier complexity with long long int was also nlogn....I know that long long int increases time but how can it be the difference between an AC and a TLE solution
link to my TLE solution:http://codeforces.com/contest/631/submission/16501208 link to AC solution:http://codeforces.com/contest/631/submission/16500604
It's not only because of LL, you've also changed cin/cout to scanf/printf
For E, I used two pointer approach in O(n) to get AC. Here is my code: http://codeforces.com/contest/631/submission/16500142
I used the fact that if i swap from position a to b(a<b), profit is (b-a)*A[a] — sum[a+1...b]. With some observation it is seen that, I want to take x, ( x>b ) as long as profit is >=0. Otherwise i start with loss which is not optimal, somewhat like kadane's algo. Also the fact is if i get b for a, then b for anew (anew > a) must be atleast as high as b and i can get optimal starting from b. So uses two pointer.
Similarly reverse the array and do same for a>b.
It's our mistake. But we found сountertest on your solution.
I used the same approach: http://codeforces.com/contest/631/submission/16493678 But failed. Can you explain why?
Thanks for fast editorial. Well, D was so tricky even in editorial :D
Thanks for the contest I really had fun though C is too tricky :P
Wow, nice contest, though I was trapped by the D's overflow of union resulting FST. - — I think D was easier than C, since it was more algorithmic ? Anyway, thanks for nice problems, especially C.
Can someone provide a more depth soln for problem C ? Failing to understand the logic .
Can someone explain how the convex hull trick solves E? The sum(l), sum(r) terms vary arbitrarily, so the given equations are not straight lines.
Take the left shift, for example:
Δl, r = (al × r - sumr) + (suml - al × l)
Note that the right part of this equation depends only on l, so if you fix l you can ignore that part when determining which delta is biggest. What remains, al × r - sumr, is clearly a straight line (x parameter is al, linear coefficient is r), so you have a different line for each possibility for r.
You still end up with 200000^2 functions (200000 for each fixed 'l'). How do you avoid processing each function?
The linear part is the same no matter which l you fix, so you only have 200000 functions (and you can use the convex hull trick to process them quickly for each l, as described in the editorial).
Thank you.
I found an O(n) solution to this problem. As we go forward we only want to add lines of increasing slope and we can trim obsolete lines off as we go. This means we can use a queue to represent the convex hull and always add to the end of the queue and read from the beginning of the queue.
Detailed explanation here
Java implementation here
Does O(n^2) solution for 631E fit time restrictions?
I'm new here, whats the reason for "-21" votes for this comment? Why does editorial contain 'solution' which is 1. trivial 2. does not fit time restrictions?
The editorial starts by explaining a O(n^2) naive solution, which is then expanded to reach a O(n log n) solution. The naive solution is included in the editorial to help people understand how one could arrive at the efficient solution. I don't know why you got downvotes for that question.
Auto comment: topic has been updated by xfce8888 (previous revision, new revision, compare).
You can also solve problem E with ternary search on integers...
more info: Ternary Search on Integers and 16498605
It's a wrong solution. We found countertest on this solution. I'm very sorry about such weak tests.
So, are all ternary search solutions wrong?
the problem still has "ternary search" tag!
My ternary search approach still gets accepted..!!!
I used ternary search to get a small range of low to high (high-low<=20) and manually checked all the positions in this range to improve the result...!! is my solution ok or the tests are that much weak??
here is my submission : http://codeforces.com/contest/631/submission/16518267
I have coded the same solution, but set wrong limits on initial answer. I am sad now.
It passed now.
I tried a ternary search solution, and it failed on test 51 :"D, it seems that authors added some new tests after the contest.
if you resubmitted your solution now, it wouldn't pass :(
Update: I got AC after modifying search space (doing ternary search twice on interval [1:i] and [i:n])
lol my solution still passes all tests.
ohh, nice :D
What's funny is your solution is trivially hackable:
Don't confuse accepted with correct. The same goes for everyone trying to argue ternary search is correct just because it passes system tests.
I know that my solution isn't correct, but I could be in top 200.
I can sympathize with that feeling, but as an unsolicited advice you should be focusing more on improvement than placement. In other words, a good use of your time would be to study and learn from this C and D so you can get top 200 without relying on luck in the future. If you can learn something from it, then this contest was definitely not a waste.
Can anyone explain to me why i am getting a TLE in my solution for C?
http://codeforces.com/contest/631/submission/16502185
O( N*log(N)*M )
Maybe authors could comment why picked so tight input limits on problem B? Basically what I don't like about it — brute-force solution wasn't cut.
Problem 631B - Print Check :
solution with O(k*n) complexity does 5*10^8 operations in the worst case, shouldn't this got AC in 1 second time limit on Codeforces ?
And I don't know why the authors picked so tight input limits, If they want a solution with better complexity. It would be better if it was (1<= n , m <= 10^5) with other constraints remain the same.
It depends on programming language and implementation. Some would be AC, some TL.
16502692
any faster solution in any language with the same complexity ?
16492693
Java faster than c++ with the same algorithm? do you have an explanation why it's faster ?
It is not exactly the same algorithm, but same complexity. Take a look at his implementation, it is actually quite a different, but still O(k * max(n, m)).
Overall I think input limits was very tight for this task.
This solution got AC in 1.4 second.
In problem D i accidentally calculated prefix function of text instead of pattern and it still passes 41 tests magically!!!
My friend implemented a brute-force algorithm for problem B but it fails (TLE) on test 23. Link to submission: http://codeforces.com/contest/631/submission/16502348
The complexity is O(k * max(n, m)), meaning 10^5 * 5 * 10^3 = 5 * 10^8. It takes approximately 1 second to process 10^9 operations. 5 * 10^8 should take approximately half a second. Am I wrong?
Edit: someone else had the same question answered. Can't delete this post so please ignore it.
Here is also a lot of I/O, which is time consuming
Could someone explain to me why my hashing solution for D is giving Wrong Answer? http://codeforces.com/contest/631/submission/16498957
Have somebody tried segment tree approach on C? I got acc with that method.
First we, as the editorial says we eliminate the queries that are overlapped totally by other front queries (that have equal or bigger Ri). So now we have a list of sort queries with descending non-repeated values of Ri that overlap partially one to each other. We can do this in O(n) if we iterate from last query to first one. Note that each query range (0,i) have some overlapped values, and some values that are not overlapped by any other query.
Then we make a segment tree from 1 to N that will have two operations solved in log(n).
Query the minimum/maximum value and it's index between two values
Change some value of segtree for other.
We'll iterate from last sequence item to the first one. In each iteration we'll do two log(n) queries that will cost us a total for the problem of o(n*log(n))
Also before anything we'll set on each item either (as a pre-computing) - It is the last item from an ascending query
So now we have three possibilities (that can be calculated in O(1) ):
The item of sequence is not part of any query, so we can leave it as it is as it was never affected for any query. This happens if there is no item at the right of array that is part of a ascending or descending query.
The last operation on the item was an ascending query. If we are marked as the last item of an ascending query or ( if we are not marked as the last item of a descending query and our right neighbor is part of a ascending query)
The last operation on the item was descending query. If the first item found at the right is part of a descending query. If we are marked as the last item of an descending query or (if we are nor marked as the last item of an ascending query and our right neighbor is part of a descending query)
If the last operation on the item was an ascending query there is only one possibility for the value of the item, that is to be the biggest value between the range (1,i), we can get this value in log(n) with the segment three. The same happens if it is a descending query. The last item is the smallest in range (1,i). So we will swap the minimum/maximum index with the item of the iteration. Nice. But now the array has changed so we need to update segment tree. To do that we will query to the segment tree to change the min/max index we have just calculated to the swapped value (that is the item of the iteration). Also we could update the other swapped value in the segment tree, but this is not necessary because in next iterations we won't touch this item again, because we now that it and all it's right items are already in their correct positions.
So final complexity o(n*log(n)) + m (the +m because the initial query computing). It is the same as the stated on editorial
16502824
Well, I have used Fenwick :P But I regret the decision :D
I think it is only worth using segtree or fenwick when you have a base pre-coded before contest. That way you only need to copy the code and use the structure functions.
Well the Fenwick is short — so it is not a problem
SegTree is much worse, anyway sometime it is just necessary — anyway I agree, it is better to use something more simple if it is possible ^_^
Morass, Could you please share how you used Fenwick?
Not bad, but, anyway, your idea to find minimum or maximum element in each step can be implemented much more easier without any data structures, Without changing and with finding min/max in O(1)
I though first about that method but that way you are not allowed to perform a query to change element value, that is vital for the algorithm. Is there any way to avoid it?
Could someone explain me why does my logic fail in test C? : http://codeforces.com/contest/631/submission/16501278
I had an idea to pick only the greatest index from 1's and 2's (which is biggest non-descending and non-ascending range) and just compute them with 2 sorts(in same order i picked them). I dont understand why would this not work,could someone explain me or atleast give me an counter case?
Thanks
Hi,
if I understood your algorithm, then it would have problem, if the last two indexes would have only low range.
lets say the managers would look like: 1 10 2 9 1 1 2 1 1 8 2 7 1 2 2 3 1 6 2 5 ~~~~~ here you would need to completely ignore 1,2,5,6 anyway you would need to use all the others {{1,10},{2,9},{1,8},{2,7},{1,6},{2,5}} (so it is more like you need to use all, which does not have bigger number after them :) )
Hope it is enough ^_^ if not, do not hesitate to ask more :)
When I try to use "custom test" to test my code with some big test using file, it always says that the character limit is exceeded.
So, I usually divide the input limit by 10, and then multiply the time by 10. Is there any way else to do it ?
How to solve Prolbem C if each time a manager can pick any arbitrary interval to sort numbers?
Editorial for this task has been updated. Now it's more detail. Also this bad sentence has been deleted.
I mean in the original problem C, each time a manager sorts the first Ri numbers, but if we modify each operations to {Ti, Li, Ri} which means to sort numbers in [Li, Ri] by order Ti (Li does not necessarily equal to 1), then this problem becomes harder than the original one and I have no idea how to solve it.
For D, I use KMP but get TLE in test 14. Can anyone help? Here is my code: 16508987
Hello, I'm afraid you can't call KMP for every single match (it would make complexity O(M*N)) (patternLen*textLen). When you have match, you have to use the KMP Fail Function :)
How can we the same problem using Z algorithm
You concatenate the "strings" (pattern.text) and use Z-function on it → by that you'll see rank of each "element" against pattern (or 1→N-1 of pattern) — then if it is as long as pattern is, you will check, whether it also 'matches' with beginning + end of pattern.
Could you please explain your solution in little more detail? I know about Z algorithm but how are you using it here to compute the rank of each "element" against pattern (1->N-1 of pattern)?
Auto comment: topic has been updated by xfce8888 (previous revision, new revision, compare).
Auto comment: topic has been updated by xfce8888 (previous revision, new revision, compare).
Auto comment: topic has been updated by xfce8888 (previous revision, new revision, compare).
Thank you very much! Best contest that I've ever written! Good Luck in Future contests!
Can someone explain me C in more detail? please
For any given position i (1<=i<=n), it is only affected by the most recent update r such that r >= i. Firstly, the integers towards the end of the array which are not affected by any updates stay as they are. Store the elements at all positions affected atleast once by some update, in a multiset. Start iterating from right to left. I keep an array upd[] which stores the most recent update at each pos. The variable 'latest_update' gets changed due to these values (if an update affects pos i, it also affects pos i-1).
When I'm at position i, I check the type of the update numbered 'last'. If it is non-decreasing, I pop the greatest element of the multiset and assign it to this position. Else if it is non-increasing, I pop the smallest element of the multiset and assign it to this position.
Please refer to my submission for implementation 16493040
Can you explain why you use your upd array ?
my solution based on that if lastChange[i] has two updates we only care about the last update and the first update don't effect any other updates.
so for every 1 <= i <= n we can update lastChange[i] as we reading all quires, and then use the same idea as yours, so what can go wrong with this ?
upd[i] stores the most recent update made such that the 'r' of the update is i. So, for all j such that 1 <= j <= i, j has been affected by that update. Alternatively you can say that the last update which affects a position i is the most recent of the updates among positions j, i <= j <= n.
As for your method, I don't think we need to care about the first update. Only the latest one should suffice.
simply Brilliant @satyaki3794. Thanks for explaining.
I solved C by starting from a simple idea, let me write it here, it may be helpful for you too. So, given array a of n numbers, if there is no any update with r=n, this means last number stays on its place forever. Analogically, we can say it for number standing at n-1, so lets keep maximum r from given data, call it maxR. and each number standing to the right of maxR, will stay on its place. Now lets keep last reordering type by index r=maxR, this means that we ordered all numbers from 1 to maxR segment, if it was non-increasing then the least number from numbers standing on (1,maxR) segment, will be standing on maxR, that's important. Or, if last reordering type was non-decreasing, then maximum number will be on maxR index. So we definitely know one more numbers' place and the same logic goes to the rest of the numbers. Now, we need to keep last update type of each index. If we update index 3 by non-increasing and then index 5 as non-decreasing, its clear that index 3 will also be updated in non-decreasing order. So we can iterate over update indexes, r-s, from last update to the first update, and keep last updates for each number. If for any moment maximum index which is somehow updated is "indx", and next update index is r, then any changes will occur if r > indx, and if that's the case, then we will keep each indexes' ordering type from indx+1 to r inclusively. There may be many questions for statements I'm using here, but they are good questions to think about also.
Did you figure out what was wrong with your solution to fail test 13 ?
I used the same idea and failed test 13 also.
Yes, I figured it out after contest. The reason was, I updated ordering for each index incorrectly. When there is some update for index i, then this update changes all numbers from 1 to i, and I forgot to consider this.
Can anyone suggest some resource to understand the implementation of E? I understood that we have to find the lower envelope of set of lines by using divide and conquer method but I am finding it very difficult to code.
I am unable to understand the solution of C. Can anybody answwer it in a more detailed way ?
What sentences from editorial you don't understood? I'll try to explain them.
For problem C in div:2 I used the above tutorial but still get TLE. :( Can anyone please modify my code to make it accepted. Thanks :) Here is my Code: http://codeforces.com/contest/631/submission/16513076
At first: look at test with such queries: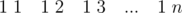 . You solution process all queries, but it should only last(look at first sentence of editorial that task). At second: try again read tutorial(some details has been added).
. You solution process all queries, but it should only last(look at first sentence of editorial that task). At second: try again read tutorial(some details has been added).
No :( for your given queries my code only process the last one.
Sorry, this part of solution is corrcet. But if we reverse previous test that count of queries would be n and count of operation that your program will be do is O(n2 * logn), because 1 + 2 + 3 + ... + n = n * (n + 1) / 2. That the reason of get TLE.
In problem C I am getting wrong answer on 14th testcase
Here is my code
This is my algo:
sort_upto : type : index
Can anyone please help me find out, where I am wrong?,
Thanks in advance :)
What is wrong here?
Can the problem E be solved by Divide-and-Conquer optimization? Just saw JoeyWheeler 's solution. Seems that he definitely don't use Convex Hull Trick.
Very interesting solution. If this solution is correct, I'm waiting from JoeyWheeler his explanation.
I'll try to stress this solution...
PS. As I see, this solution has O(n·log2(n)) complexity.
It's not hard to explain this solution. First, traditional divide-and-conquer idea: either the optimal move crosses the middle of the array or it doesn't. If it doesn't cross, we can solve the problem recursively for both halves, so let's only consider the crossing case, in which you move element from one half to a position in the other half.
Each value a[i] in the first half has an optimal position opt[i] in the second half it should be moved to. Crucial observation: if a[i] < a[j], then opt[i] <= opt[j]. In other words, the smaller the element, the more to the left it should be in an optimal move. I think it's intuitively obvious that this is true, but it's also easily proven if you're doubting it. This condition is also the condition for the divide-and-conquer optimization, which we can apply to find optimal half-crossing move for all i in O(n log n).
A more interesting question is how he thought of that before thinking of the convex hull idea. I guess that's why he's the LGM and I'm not...
Can we solve problem D using z algorithm
I think it might be possible if you concatenate the strings (and the do it cleverly :) )
Yes it can be done. Check my solution
It's very easy. Remove first and last blocks from s. Find all matches of string s using Z-function or another fast algorithm. Don't forget to check removed first and last blocks in each occurrence.
In Problem D, I was looking at the solution, and it says that the complexity is O(n+m). But I don't get it since see this: ~~~~~
for (int i = 1, j = 0; i < n — 1; i++) { while (j > 0 && !(b[j + 1] == a[i])) j = pi[j];
~~~~~ So you may take a lot of step back. Why isn't it shown in complexity?
Actually it is shown in the complexity. The pi[] is fail function and by this function you can go back only by "limited" number of steps. This pi can "increase" only by one per index, making it N max. That means that the "while" cycle will proceed at most "n" times (during the whole algorithm).
Can anyone tell me if I correctly understand problem E? if there is a sequence of 7
1 6 2 5 3 7 4
The accepted solutions I found produce 132 as output. Shouldn't the answer be 133, by moving 6 to the end? and have this sequence : 1 2 5 3 7 4 6 = 1*1 + 2*2 + 5*3 + 3*4 + 7*5 + 4*6 + 6*7 = 1 + 4 + 15 + 12 + 35 + 24 + 42 = 133. My code got WA and I'm just trying some test cases. Any explanation of my misunderstanding would be great. Thanks.
The accepted solutions you found are incorrect, the answer is 133 according to the official solution above. System tests were weak, so many wrong algorithms (especially ternary search) got accepted when they shouldn't.
Oh I see, that's why there are many wrong outputs although it got ac. Thanks for the clarification!
There is actually a probabilistic algorithm for D :
The goal is to create an "additive" hash function. Id the string is w0w1... wn then the hash of this string is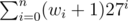 modulo a big prime (we use + 1 that even a's have a "weight". Now our algorithms becomes :
modulo a big prime (we use + 1 that even a's have a "weight". Now our algorithms becomes :
Read and compress input as much as possible (i.e. transform all adjacent blocks of same character into a single block)
Calculate the hash for the beginning block to all other blocks. This can be done in . Note that we use an logarithmic algorithm to compute powers modulo something and that
. Note that we use an logarithmic algorithm to compute powers modulo something and that 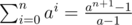 . Also note that you will have to compute some modular inverses. This step can be made even faster by precomputing all the needed powers.
. Also note that you will have to compute some modular inverses. This step can be made even faster by precomputing all the needed powers.
If the second string is one block, then it is trivial. Otherwise, check for each possible starting conditions, if the beginning and the end do make sense and the hash of the interior of both strings equals. Note that you can find a hash in linear time by the precomputation we did.
This algorithm has got an AC. However, the algorithm will not be correct in all possible test cases : there might be two different strings that have the same hash, yielding to a final answer that is too big. One might try to output the min of executions with different primes. Finally, we could try to prove that a certain set of primes will be enough — I don't know how to do this however. I would be very happy to discuss this idea with someone!
Here is my (very dirty) implementation, after a lot of rather stupid mistakes... 16651442
My implementation is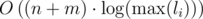 . However, you can speed this up by precomputing all the powers of the inverse of 27 - 1. In that case, it would become O(n + m + max(li)).
. However, you can speed this up by precomputing all the powers of the inverse of 27 - 1. In that case, it would become O(n + m + max(li)).
What do you think about this approach?