A — Vasya and the Bus
Firstly, if n = 0, then children can't be in the bus, so if m = 0 then the answer is (0, 0), otherwise the answer is "Impossible". Now n > 0. If m = = 0, than it is only one possible variant of passage — the answer is (n, n). Otherwise, more grown-up take some children, less the sum that people pay. So, if only one adult takes all children, than we get maximal sum — n + m - 1. Maximum min(n, m) adults can take the children with them, so the minimal answer is n + m - min(n, m) = max(n, m).
B — Surrounded
Let's find the minimum distance between two circles L. Then the answer to our problem is L / 2.
Now d is the distance between the centers of the circles, R, r — their radiuses. There are 3 possible cases:
- Circles don't intersect. Then L = d - R - r. Firstly, it's reachable: let's consider the segment, connecting the centers of the circles, and take its part, which is out of both circles — its length is exactly d - R - r.









 Let's prove that lesser distance is impossible. If the segment connecting two points of distinct circles have length l, than R + l + r > = d, so l > = d - R - r.
Let's prove that lesser distance is impossible. If the segment connecting two points of distinct circles have length l, than R + l + r > = d, so l > = d - R - r.




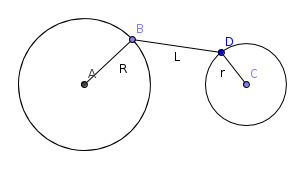
- If one circle is into another, than analogically the answer is R - d - r, where R is the radius of the bigger circle.
- If the circles intersect, then the answer is 0.
C — STL
In this problem we have an array of strings (s1, s2, ...sn), where si = pair or int.
Let's consider bali = the difference between number of "pair" and "int" int the subarray (s1, s2, ...si).
Than we can prove that the type can be reestablished from the array s < = > bali > = 0 for 1 < = i < n and baln = - 1. This can be proved using mathematical induction, the parameter is the number of "int"-s in the array.
And how to find the solution, if we know that is exists? Consider the function gettype(inti), which builds the type beginning in the position i and returns the index, next to the position where it finished building of type. How it works? If si = "int", then the function prints "int" and returns i + 1. Else it prints "pair < ", gettype(i + 1) is launched, let it returns j. Then we print ", " and launch gettype(j) (it returns k), then we print " > " and return k.
We can not to do check if the type can be reestablished from the array in the beginning: launch gettype() and print "Error occurred" if there became some contradiction during the building of type.
D — Non-secret Cypher
First solution: Let's use the method of two pointers. For every number we will know how many times it occurs in the current segment [l, r]. For fixed l we increase r until a[r] occurs in the current segment less than k times. If a[r] occurs int the segment [l, r] k times, we add to the answer all segments [l, t] for all t > = r and increase l (and do not forget to decrease the number of a[l] in the current segment).
To keep the number of every value in the segment we can use map or compression of the coordinates. Also it's important not to forget that the maximal answer is 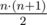 , which doesn't fit in int.
, which doesn't fit in int.
Second solution: firstly, let's do the compression of the coordinates. For every value X we write the list of the positions i such that a[i] = X. Now using that we fill the array b: b[i] is the minimum index that segment [i, b[i]] contains k numbers equal to a[i] (obviosly, a[b[i]] = a[i]), if this index doesn't exist, then b[i] = n + 1.
Let's find for every index i a minimal index j such that segment [i, j] contsins k equal numbers (if such j doesn't exist, we say that j = n + 1) — then we add to the answer n + 1 - j. This j is equal to 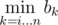 . All that minimums can be found in a single pass through a from its end. Then we can sum the answers for all indexes 1 < = i < = n.
. All that minimums can be found in a single pass through a from its end. Then we can sum the answers for all indexes 1 < = i < = n.
The complexity of these solutions is O(nlogn).
E — Counter Attack
This problem has several different solutions. Anyway, we should consider towns as the vertices of the graph, roads as its edges. Now we are to find the connected components of the complementary graph (CG) of the given graph. Let's take the vertex A with the minimal degree c: 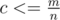 . We call the set of the vertices who are connected with A — B, that are not connected — D . All vertices which don't connect with A will be in the same connected component of the CG. Let's build the complemented graph to the subgraph including A and set B — there are
. We call the set of the vertices who are connected with A — B, that are not connected — D . All vertices which don't connect with A will be in the same connected component of the CG. Let's build the complemented graph to the subgraph including A and set B — there are 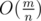 vertices and
vertices and 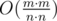 =
= 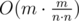 = O(m) edges.
= O(m) edges.
Let's build DSU for the vertices of given graph and merge components which we have found using the new-built graph. All that we should do after it is to consider vertices from B: now we look to the vertex v. We put v in the same component as A if v has edges not to all vertices of D (we do it using DSU too). The complexity of this solution is O(m) or O(mlogn).
Another solution: we keep set a, which contains vertices, which haven't been visited yet. Let's run series of bfs to find the components of CG. If we are working now with the vertex v, pass through a. Consider u is the element of a. If edge (u, v) isn't in the given graph, than u is in the same component of CG as v, so, we can erase it from a and add to queue. Otherwise, we do nothing.
What is the complexity of this solution? To understand that, we must know how many times whe consider fixed vertex u in the set a. u remains int a when we run to them from vertex v < = > edge (u, v) is in the given graph. So, every vertex u remains in a no more than its degree. So, the complexity of this algorithm is O(mlogn) (log n because of binsearch — we need use it to know, is (u, v) in the graph). If we use HashMap, we'll get O(m).











In description of B propably is a typo: "one circle is into another" appears for two of three cases
thank you, fixed now
I think that the limits of problem C are a little bit strict, My solution got TLE on case 8 and it goes like this: - create a stack of string - loop over the tokens from the end to the beginning - step 1: if it is a token "int" then add it to the stack - otherwise - step 2: as it is a token "pair" then take the last two elements s1 and s2 ,remove them from the stack and then push into the stack the following string s = "pair<" + s1 + "," + s2 + ">" - in case that in step 2 there are not two strings to take from the stack or the stack doesn't contain exactly 1 element at the end of the process then the input string is invalid. My algorithm failed because the concatenation is really costly. I could have made it better but that is what I first thought at contest.
Concatenation is O(N), so your overall solution would have O(N^2) complexity. I don't think adding a couple of seconds to the time limit is going to fix that.
I don't understand the complexity analysis for the 2nd solution for problem E. Each vertex u remains in a no more than it's degree, but it's degree could be m right? So isn't the complexity then O(m^2 logn) ?
Degree of one vertex can be m, but sum of all degrees for all vertexes is 2 * m.
would u please explain what does DSU mean?
Disjoint-set union (or disjoint-set data structure)
thank you
I have a problem with task E. I am writing in Java and I get TLE on test 12. Here is my code http://codeforces.com/contest/190/submission/10214647 . There are only 3-4 accepted Java codes, but they used BFS soluton with binary search insted of DSU. I am using hashset instead of list with binary search, so it should run faster. How can I improve this ?
My solution
Problem E can be also solved using binary indexed trees. My solution runs in
O(m+n log^2 n), but this idea can be reduced toO(m+n log n).Can you plz share your approach?
i'm getting tle at problemE:Counter Attack on test case 12. Here is my code. Do you suggest any improvement? I'm using the 2nd approach explained at the editorial.
The C problem can be done by maintaining a stack. Maintain a brace_count array and a comma array of size as large as the input, they will tell us the number of end braces and comma required in the answer string. As you're reading the input: 1.) if the input is a pair push 0 into the stack. 2.) if the input is an int: i.) if the top is 0 make it 1, and put comma[i]=1. ii.) if the top is 1 a.) make brace_count[i]++ (for putting the as the pair is completed now b.) keep popping until the top becomes 0 and then go to a.) again. if the stack is non-empty or it becomes empty during the reading process, then there is an error. For printing the answer: 1.) start printing from the input, if comma[i]==1 print a comma after it,if the brace_count[i] is not 0 start printing the endbraces between input and comma. if there is a pair in input put an opening brace after it