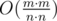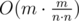Hello!
Traditionally AIM Tech organizes a big party for Petrozavodsk camp participants to have fun and get an opportunity to communicate with each other. Usually it comes along with a funny contest in unusual format. This year we decided to share the fun with all codeforces community!
This year we came up with a format requiring (probably) less time for preparing the contest. It is somewhat similar to an ordinary contest with a 3-hour duration. We already have some problem ideas, so it should be super easy to prepare the problems just one night before the competition. We hope everything will run smoothly!
The contest will start on Feb/03/2020 19:15 (Moscow time). It could be a bit rescheduled due to onsite delays.
It will be an unrated funny competition. Unlike usual ICPC-style contests, you'll be given an archive with several open test cases and answers for each problem. You'll have some sample test cases in the statement too, they'll be included in the archive. However, the solutions will be tested against both open and hidden tests. The open tests will be published as an encrypted zip-archive in this post. The password will be published just before the start of the contest.
The statements will be in English only because we are running out of time in preparation and have to prioritize things.
It's not 100-percent clear at the moment, but it seems the contest will be somewhat hard, so we recommend it for div. 1 participants. However, div. 2 participants are welcome as always, but we can't guarantee the contest will be a perfect match for them.
It's possible to participate both individually and in teams of maximum 3 persons.
Another point to mention is that the order of problems could be not the same as the order of their difficulties. But we'll try to do so. A bit.
The authors to blame are Kostroma, zemen, Golovanov399, mathbunnyru and ArtDitel.
As you may notice, it is just one night before the competition, so we should start preparing the problems. We hope that we'll manage not to do very stupid bugs in the tests. See you at the competition!
UPD It's still more than 4 hours before the contest, but the open tests are already prepared! You can download the archive using one of the two links: one two. The encrypted archive contains another archive containing the actual tests.
The password will be published here shortly before the start of the contest.
UPD2 We have to move contest 10 minutes forward, because we need to prepare the last problem :(
UPD3 Oops, the contest is about to start, but we still don't have correct solutions! Unfortunately, each authors' solution contains a bug (or even several bugs!). However, we decided not to cancel the competition. We give you the outputs of the model solutions on open tests in the archive. Guess all the bugs in our solutions and get OK for the code with exactly same bugs! Good luck and have fun!
The password to the archive will be published as a clarification in the contest interface.
UPD4 The password to the archive is oops_seems_that_nobody_tested_the_solutions
UPD5 The editorial is published, but it still does contain bugs, wait a bit while it is being debugged.
UPD6 Feel free to share your opinion in the comments! Were the solutions enough buggy? Was it enough hard, or we should've added a couple of hard problems? Do you want to solve such contests in future?









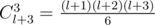 — the total number of ways to increase the sticks not more than
— the total number of ways to increase the sticks not more than 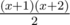 different ways (again we divide
different ways (again we divide 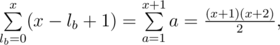
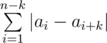 , we can consider each group separately and sum the distances between neighbouring numbers in each group.
, we can consider each group separately and sum the distances between neighbouring numbers in each group. 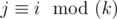 . Let's write down its numbers from left to right:
. Let's write down its numbers from left to right: 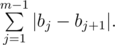
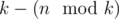 groups of size
groups of size 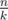 (so called small groups) and
(so called small groups) and 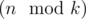 groups of size
groups of size 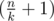 (so called large groups). Consider the following dynamic programming:
(so called large groups). Consider the following dynamic programming: 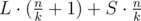 elements of the sorted array
elements of the sorted array 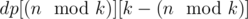 .
.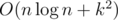 . We can note that in pretests
. We can note that in pretests 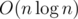 ),
), 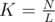 .
.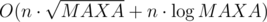 time.
time. . Base for
. Base for 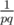 , that is
, that is  , that's we wanted to prove.
, that's we wanted to prove.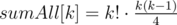 . The prove is simple: let's change in permutation
. The prove is simple: let's change in permutation 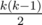 , and our conversion of the permutation is a biection.
, and our conversion of the permutation is a biection.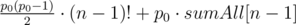 inversions.
inversions.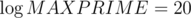 intervals, because for each
intervals, because for each 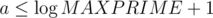 . Practically there is no more than
. Practically there is no more than 

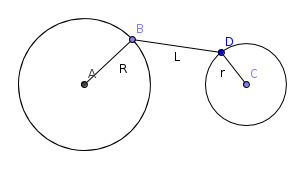
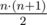 , which doesn't fit in
, which doesn't fit in 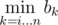 . All that minimums can be found in a single pass through
. All that minimums can be found in a single pass through 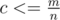 . We call the set of the vertices who are connected with
. We call the set of the vertices who are connected with 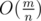 vertices and
vertices and