Here is git repository to solutions of problems of this contest.
Div.2 A
You should check two cases for YES:
- x mod s = t mod s and t ≤ x
- x mod s = (t + 1) mod s and t + 1 < x

Time Complexity: 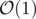
Div.2 B
Nothing special, right? just find the position of letters . and e with string searching methods (like .find) and do the rest.

Time Complexity: 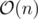
A
Do what problem wants from you. The only thing is to find the path between the two vertices (or LCA) in the tree. You can do this in 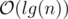 since the height of the tree is
since the height of the tree is 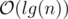 . You can keep edge weights in a map and get/set the value whenever you want. Here's a code for LCA:
. You can keep edge weights in a map and get/set the value whenever you want. Here's a code for LCA:
LCA(v, u):
while v != u:
if depth[v] < depth[u]:
swap(v, u)
v = v/2 // v/2 is parent of vertex v

Time Complexity: 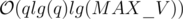
B
First of all starting_time of a vertex is the number of dfs calls before the dfs call of this vertex plus 1. Now suppose we want to find the answer for vertex v. For any vertex u that is not in subtree of v and is not an ancestor v, denote vertices x and y such that:
- x ≠ y
- x is an ancestor of v but not u
- y is an ancestor of u but not v
- x and y share the same direct parent; That is par[x] = par[y].

The probability that y occurs sooner than x in children[par[x]] after shuffling is 0.5. So the probability that starting_time[u] < starting_time[v] is 0.5. Also We know if u is ancestor of v this probability is 1 and if it's in subtree of v the probability is 0. That's why answer for v is equal to 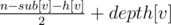 (depth is 1-based and sub[v] is the number of vertices in subtree of v including v itself). Because n - sub[v] - h[v] is the number of vertices like the first u (not in subtree of v and not an ancestor of v).
(depth is 1-based and sub[v] is the number of vertices in subtree of v including v itself). Because n - sub[v] - h[v] is the number of vertices like the first u (not in subtree of v and not an ancestor of v).
Thus answer is always either an integer or an integer and a half.
Time complexity: 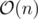
C
It gets tricky when the problem statement says p and q should be coprimes. A wise coder in this situation thinks of a formula to make sure this happens.
First of all let's solve the problem if we only want to find the fraction  . Suppose dp[i] is answer for swapping the cups i times. It's obvious that dp[1] = 0. For i > 0, obviously the desired cup shouldn't be in the middle in (i - 1) - th swap and with this condition the probability that after i - th swap comes to the middle is 0.5. That's why
. Suppose dp[i] is answer for swapping the cups i times. It's obvious that dp[1] = 0. For i > 0, obviously the desired cup shouldn't be in the middle in (i - 1) - th swap and with this condition the probability that after i - th swap comes to the middle is 0.5. That's why 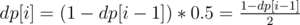 .
.

Some people may use matrix to find p and q using this dp (using pair of ints instead of floating point) but there's a risk that p and q are not coprimes, but fortunately or unfortunately they will be.
Using some algebra you can prove that:
- if n is even then
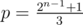 and q = 2n - 1.
and q = 2n - 1. - if n is odd then
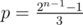 and q = 2n - 1.
and q = 2n - 1.
You can confirm that in both cases p and q are coprimes (since p is odd and q is a power of 2).
The only thing left to handle is to find 2n (or 2n - 1) and parity. Finding parity is super easy. Also 2n = 2a1 × a2 × ... × ak = (...((2a1)a2)...)ak. So it can be calculated using binary exponential. Also dividing can be done using Fermat's little theorem.
Time complexity: O(klg(MAX_A)).
D
Build the prefix automaton of these strings (Aho-Corasick). In this automaton every state denotes a string which is prefix of one of given strings (and when we feed characters to it the current state is always the longest of these prefixes that is a suffix of the current string we have fed to it). Building this DFA can be done in various ways (fast and slow).
Suppose these automaton has N states (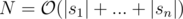 ) and state v has edges outgoing to states in vector neigh[v] (if we define our DFA as a directed graph). Suppose state number 1 is the initial state (denoting an empty string).
) and state v has edges outgoing to states in vector neigh[v] (if we define our DFA as a directed graph). Suppose state number 1 is the initial state (denoting an empty string).
If l was smaller we could use dp: suppose dp[l][v] is the maximum score of all strings with length equal to l ending in state v of our DFA when fed into it.
It's easy to show that dp[0][1] = 0 and dp[1][v] ≤ bv + dp[l + 1][u] for u in neigh[v] and calculating dps can be done using this (here bv is sum of a of all strings that are a suffix of string related to state v).

Now that l is large, let's use matrix exponential to calculate the dp. Now dp is not an array, but a column matrix. Finding a matrix to update the dp is not hard. Also we need to reform + and * operations. In matrix multiplying we should use + instead of * and max instead of + in normal multiplication.
Time complexity: 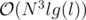 .
.
E
First of all, for each query of 1st type we can assume k = 1 (because we can perform this query k times, it doesn't differ).
Consider this problem: there are only queries of type 1.
For solving this problem we can use heavy-light decomposition. If for a vertex v of the tree we denote av as the weight of the lightest girl in it (∞ in case there is no girl in it), for each chain in HLD we need to perform two type of queries:
- Get weight of the lightest girl in a substring (consecutive subsequence) of this chain (a subchain).
- Delete the lightest girl in vertex u. As the result only au changes. We can find this value after changing in
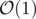 if we have the sorted vector of girls' weights for each vertex (and then we pop the last element from it and then current last element is the lightest girl, ∞ in case it becomes empty).
if we have the sorted vector of girls' weights for each vertex (and then we pop the last element from it and then current last element is the lightest girl, ∞ in case it becomes empty).

This can be done using a classic segment tree. In each node we only need a pair of integers: weight of lightest girl in interval of this node and the vertex she lives in (a pair<int, int>).
This works for this version of the problem. But for the original version we need an additional query type:
3. Increase weight of girls in a substring (consecutive subsequence) of this chain (a subchain) by k.
This can be done using the previous segment tree plus lazy propagation (an additional value in each node, type 3 queries to pass to children).
Now consider the original problem. Consider an specific chain: after each query of the first type on of the following happens to this chain:
- Nothing.
- Only an interval (subchain) is effected.
- Whole chain is effected.
When case 2 happens, v (query argument) belongs to this chain. And this can be done using the 3rd query of chains when we are processing a 2nd type query (effect the chain v belongs to).
When case 3 happens, v is an ancestor of the topmost vertex in this chain. So when processing 1st type query, we need to know sum of k for all 2nd type queries that their v is an ancestor of topmost chain in current chain we're checking. This can be done using a single segment/Fenwick tree (using starting-finishing time trick to convert tree to array).
So for each query of 1st type, we will check all chains on the path to find the lightest girl and delete her.
Time Complexity: 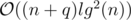
F
In the first thoughts you see that there's definitely a binary search needed (on r). Only problem is checking if there are such two points fulfilling conditions with radius r.
For each edge, we can shift it r units inside the polygon (parallel to this edge). The only points that can see the line coinciding the line on this edge are inside the half-plane on one side of this shifted line (side containing this edge). So problem is to partition these half-planes in two parts such that intersection of half-planes in each partition and the polygon (another n half-planes) is not empty. There are several algorithms for this propose:
 Algorithm:
Algorithm:

It's obvious that if intersection of some half-planes is not empty, then there's at least on point inside this intersection that is intersection of two of these lines (lines denoting these half-planes). The easiest algorithm is to pick any intersection of these 2n lines (n shifted half-planes and n edges of the polygon) like p that lies inside the polygon, delete any half-plane containing this point (intersection of deleted half-planes and polygon is not empty because it contains at least p) and check if the intersection of half-planes left and polygon is not empty (of course this part needs sorting half-planes and adds an additional log but we can sort the lines initially and use something like counting sort in this step).
Well, constant factor in this problem is too big and this algorithm will not fit into time limit. But this algorithm will be used to prove the faster algorithm:
 Algorithm:
Algorithm:
In the previous algorithm we checked if p can be in intersection of one part. Here's the thing:
Lemma 1: If p is inside intersection of two half-planes (p is not necessarily intersection of their lines) related to l - th and r - th edge (l < r) and two conditions below are fulfilled, then there's no partitioning that in it p is inside intersection of a part (and polygon):
- At least one of the half-planes related to an edge with index between l and r exists that doesn't contain p.
- At least one of the half-planes related to an edge with index greater than r or less than l exists that doesn't contain p.
Because if these two lines exist, they should be in the other part that doesn't contain p and if they are, intersection of them and polygon will be empty(proof is easy, homework assignment ;)).

This proves that if such partitioning is available that p is in intersection of one of them, then it belongs to an interval of edges(cyclic interval) and the rest are also an interval (so intersection of both intervals with polygon should be non-empty). Thus, we don't need p anymore. We only need intervals!
Result is, if such partitioning exists, there are integers l and r (1 ≤ l ≤ r ≤ n) such that intersection of half-planes related to l, l + 1, ..., r and polygon and also intersection of half-planes related to r + 1, r + 2, ..., n, 1, 2, ..., l - 1 and polygon are both non-empty.
This still gives an 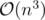 algorithm (checking every interval). But this lemma comes handy here:
algorithm (checking every interval). But this lemma comes handy here:
We call an interval(cyclic) good if intersection of lines related to them and polygon is non-empty.
Lemma 2: If an interval is good, then every subinterval of this interval is also good.
Proof is obvious.
That gives and idea:
Denote interval(l, r) is a set of integers such that:
- If l ≤ r, then interval(l, r) = {l, l + 1, ..., r}
- If l ≤ r, then interval(l, r) = {r, r + 1, ..., n, 1, ..., l}
(In other words it's a cyclic interval)
Also MOD(x) is:
- x iff x ≤ n
- MOD(x - n) iff x > n
(In other words it's modulo n for 1-based)
The only thing that matters for us for every l, is maximum len such that interval(l, MOD(l + len)) is good (because then all its subintervals are good).
If li is maximum len that interval(i, MOD(i + len)) is good, we can use 2-pointer to find values of l.
Lemma 3: lMOD(i + 1) ≥ li - 1.
Proof is obvious in result of lemma 2.
Here's a pseudo code:
check(r):
len = 0
for i = 1 to n:
while len < n and good(i, MOD(i+len)): // good(l, r) returns true iff interval(l, r) is good
len = len + 1
if len == 0:
return false // Obviously
if len == n:
return true // Barney and Lyanna can both stay in the same position
l[i] = len
for i = 1 to n:
if l[i] + l[MOD(i+l[i])] >= n:
return true
return false
good function can be implemented to work in 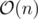 (with sorting as said before). And 2-pointer makes the calls to good to be
(with sorting as said before). And 2-pointer makes the calls to good to be 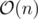 .
.
So the total complexity to check an specific r is 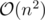 .
.
Time Complexity: 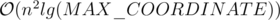
Feel free to comment and ask your questions.












No matter what number of problems I have solved on probability I won't be able to solve it :D
It was easy to know there was some formula on levels , subtree sizes etc. but yet I failed =(
Fastest editorial ever,
BTW, Hack test case for Div2 B is "1.0e0".
In problem B, "d contains no trailing zeros" could basically mean that d can have leading 0s. For example, 0.0001e1 should be printed as 0.001; 0.01e2 as 1; 0.01e5 as 1000; and 1.02e5 as 102000.
d can never be non-zero when a is zero. So 0.0001e1 is an invalid input.
How fast the tutorial is !
Wow! Editorial is published so quickly.
Lightning fast editorial! Fun contest (even though I am horrible in controlling trees so I couldn't solve C and D)
For Div 2 E, I was stuck on how to power 2s, (I knew the logarithm time trick but I didn't know how to stack the powers since there is the 2^{n-1} stuff and all that) so I decided to make a inverse table..
Fun contest. Thank you!
Tried to hack solution A(div.2):
int cur = t; while (cur < x) { cur += s; if (check(cur)) { found(); break; } }
by test: t = 0, s = 2 x = 1e9 can't get why this solution get AC on this test, not TLE. :\
Result of hacking: Failed
I don't see why this would result in TLE. A solution with O(n) where n = 5e8 (or 1e9) can run in less than 1 second. Why do you think this should be TLE?
Usually the golden rule is that a computer can handle around 107 operations in around one second. However, this applies to big-O analises because it usually omits a lot of constants. In this case, it's just a simple loop, so 109 operations run easily in one second.
Is there a way to solve div1A without hash maps? I got the path part fairly quickly but I was unable to store the costs of the roads and search for them efficiently. Using arraylists to store the paths and search the costs is on the order of 128k^2 and won't run in time.
before every query of type 2 you can sort your edge weight array and then use binary search to look for the edges in path of u-v for the current query. The only thing to take note is that as you are storing in the array there will be multiple instances of the same edges with same/different weights, so after binary search when you find your edge just look to the left and right of the element until you get different edge and keep adding the weights to the answer. I myself code in C so came up with this solution but was too lazy to code so don't know whether it will pass or not :P
I tried this with a little modification and it just barely ran under time. My modification is that instead of sorting before every query of type 2, instead, only sort before a query of type 2 when there has been a query of type 1 that could have possibly messed up the sorting pattern. This only requires one
bool sortedand two lines of code, but without this, it will not run under time.The worst case for this is complete alternating between queries 1 and 2. For query 1s, we just have for each query since each edge can be processed in constant time, so this gives us the term
for each query since each edge can be processed in constant time, so this gives us the term 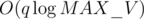 . For query 2s, from query 1s, we have
. For query 2s, from query 1s, we have 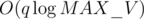 , so sorting is
, so sorting is 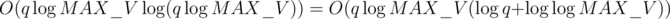 and we do this for O(q) queries. However, there are
and we do this for O(q) queries. However, there are  edges between two nodes and we need to do a binary search for each edge, this gives us
edges between two nodes and we need to do a binary search for each edge, this gives us 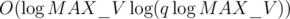 and we need to do this for O(q) queries. Finally, we need to account for duplicate edges. Since we will only encounter each edge once, the duplicate edges overall only take up O(q) time for each query, so it's O(q2) overall. In total, we get
and we need to do this for O(q) queries. Finally, we need to account for duplicate edges. Since we will only encounter each edge once, the duplicate edges overall only take up O(q) time for each query, so it's O(q2) overall. In total, we get 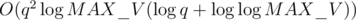 since that's the biggest term we get, which is from the sorting. Using q = 1000 and MAX_V = 1018, we get about O(9.5*10^7) which explains why this is just under a second since O(10^8) is usually just under a second because of a constant factor of around 10-30 operations times the number in the O-analysis.
since that's the biggest term we get, which is from the sorting. Using q = 1000 and MAX_V = 1018, we get about O(9.5*10^7) which explains why this is just under a second since O(10^8) is usually just under a second because of a constant factor of around 10-30 operations times the number in the O-analysis.
This is faster than the array list solution, which is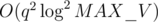 . However, using a binary search tree like
. However, using a binary search tree like  edges for
edges for 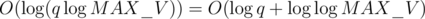 time for O(q) queries, giving us
time for O(q) queries, giving us 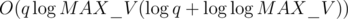 taking a way the whole factor of O(q) from our solution. However, the editorial ignores the
taking a way the whole factor of O(q) from our solution. However, the editorial ignores the 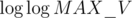 part because it is smaller than the
part because it is smaller than the 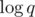 term.
term.
mapfrom the STL is still better because we simply need to processAbout Div 1 C, what I noticed about the numerator after generating a couple of answers and using the power of OEIS, is that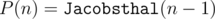 . And
. And 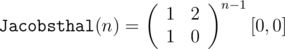 , so we can still find this in logarithmic time if you (like me) missed the formula given in the editorial.
, so we can still find this in logarithmic time if you (like me) missed the formula given in the editorial.
I tried doing this, but it gave me TLE and was much more complex to code. I guess the formula of the editorial is the simplest way!
Also, the editorial's formula is also on the OEIS page for Jacobsthal.
I got AC with stupid optimisations,the limits are strict for B and C div 1.
I also solved this problem same way as you. The only difference is I am applying Fermat little theorem, which helps to further reduce time complexity to O(log 10^9 + 7)
Hello, there! How dou you apply Fermat's little theorem here? Can you explain a little, please?
we have a^p = a (mod p) with p is prime, so with n = k*p + x, we have a^n = a^(k*p)*a^x. Notice that a^(k*p) = a^p*a^p ... = a^k (mod p), so, we can continue to factorize k = h*p + y ... until we got something that less than p, then we stop.
You can take a look at my submission
In Div1C, heavy artillery to find the answer :)
=> formula is 1 / 3 * 1K + 2 / 3 * ( - 1 / 2)K
Hah nice :). In fact that was a recurrence of form "x_n and y_n are linearly dependent on x_{n-1} and y_{n-1}" and such recurrence can be transformed to recurrence "x_n is linearly dependent on x_{n-1} and x_{n-2}" and there are known methods for solving them (yours included :P).
For problem E, one can find the product modulo 1e9+6 and then use binary exponentiation instead of repeated exponentiation.
EDIT: It doesn't seem to work, I thought I made an implementation error during the contest but fixing that doesn't get AC. :/
http://codeforces.com/contest/697/submission/19133170
EDIT2: Previous code had overflow issues. Here's the fixed AC code:
http://codeforces.com/contest/697/submission/19133853
In Div1C, xmod - 1 = 1 for any numbers or matrices so you can just calculate the "value" in mod and do something. It will be O(N).
Nice!
The "for any matrices" part is not true. For example we may consider Fibonacci numbers matrix F=[1,1;1,0] and mod=13. F^12 (mod 13)=[233, 144;144,48] (mod 13) = [12,1;1,11]. And the least power, for which F^k (mod 13) = [1,0;0,1] is k=28. And it's even not divisible 12.
It may work in this particular problem, but won't work in general.
Wow! Then, it's just coincide or there're some conditions for this? I was pretty sure when I was writing this.
I don't know. Just guessed that there may be problems, when there is no square root of 5 for Fibonacci numbers. And 13 was a suitable one.
If we have a sequence x[n]=A x[n-1], all eigenvalues of A exist and distinct mod P and none of them equals to 0 mod P, then it will definitely be periodic with period that is a divisor of p-1. Thus Ap - 1 = I (mod p). Can't say anything more general.
You might find interesting part about Pisano period here.
The reason is that roots of characteristic polynomial exist in field modulo prime, though they are integers in this problem. On the other cases such statement is wrong.
Any problems similar to div2D / div1B ?
LCA I use for D2.C / D1.A:
What is
int(math.log2(2 ** 49 - 1))in Python?IT'S 49...
Then look at your exploded prob A.
it indeed is 49 my friend !!
Yes, for some weird reason, (int)(log2((1LL<<49)-1)) is 49 in C++ as well. :(
C++ likely has the same rounding error as Python. Do not cast the
intand then print it. You should get49.000000.This is called "rounding error." Leave out the
int()and you'll getmath.log2(2 ** 49-1) == 49because Python rounds the floating point number to49. Instead, you should do a binary search on the array[1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768, 65536, 131072, 262144, 524288, 1048576, 2097152, 4194304, 8388608, 16777216, 33554432, 67108864, 134217728, 268435456, 536870912, 1073741824, 2147483648, 4294967296, 8589934592, 17179869184, 34359738368, 68719476736, 137438953472, 274877906944, 549755813888, 1099511627776, 2199023255552, 4398046511104, 8796093022208, 17592186044416, 35184372088832, 70368744177664, 140737488355328, 281474976710656, 562949953421312, 1125899906842624, 2251799813685248, 4503599627370496, 9007199254740992, 18014398509481984, 36028797018963968, 72057594037927936, 144115188075855872, 288230376151711744, 576460752303423488, 1152921504606846976].That's very weird same code in my compiler (sublime text ) shows correct output but not on codeforces.
Is that a problem from codeforces judging system or my IDE?
I had similar problems a week ago. I'm not sure it downcastes right. Try using floor indead.
I had this same problem during the contest, but I realized that the problem was because I was using long instead of long long which was OK on my computer, but not on CodeForces' servers. Make sure you are not having any integer overflow and all of your types are correct. CodeForce's custom test is helpful for debugging this.
I need some help with Div.2 D...
Let v, u, x, y be vertices as the editorial says. I understand that the probability of starting_time[u] < starting_time[v] is 0.5. And I get that, if u is an ancestor of v, then this probability is 1, and if u is in the subtree of v, then this probability is 0.
But I can't understand why these facts imply that the answer for v is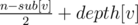 .
.
Check this, the approach is a bit different: http://codeforces.com/blog/entry/45991?#comment-305083
We will denote E(v) as the expected time value of vertex v (the answer for v).
Then, we will compute the answer based on the probabilty that each vertex u ≠ v is visited before v. So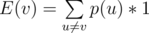 , where p(u) is the probability that u is visited before v. Then we will have p(u) = 1 in case u is an ancestor, p(u) = 0 in case u is a children and else we will have p(u) = 1 / 2 .
, where p(u) is the probability that u is visited before v. Then we will have p(u) = 1 in case u is an ancestor, p(u) = 0 in case u is a children and else we will have p(u) = 1 / 2 .
We have depth[v] nodes with p(u) = 1 and n - sub[v] - (depth[v] - 1) nodes with p(u) = 1 / 2, which leads us to the formula.
Edit: Actually formula on the editorial was wrong, it should be n - sub[v] - (depth[v] - 1), where depth begins at 1.
Thanks, really cool idea and implementation!
sorry to bother. can you explain more on how did you get formula
E[v] = sigma p[u] * 1 : u != v?? all i know is thatE[X] = sigma x p(x)such that X is a random variable. what i think is that here for a fixed v, let X be a random variable of the value of starting_time[v]. now we should calculate the probabilities. p(1) = the probability that starting_time[v] = 1 , p(2) = the probability that starting_time[v] = 2, ... then we will haveE[v] = sigma p(x) * x : x >= 1. so how did you get your formula? did you use another random variable or what?Suppose we generate all possible arrays for dfs in-order permutation, all of then equiprobable. Let's denote tv the time of vertex v and N the number of permutations we computed.
You agree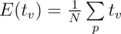 ? Where tv is the value a given vertex would have in permutation p.
? Where tv is the value a given vertex would have in permutation p. 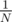 is outside summation because all permutations are equiprobable, so all of them have probabilty
is outside summation because all permutations are equiprobable, so all of them have probabilty 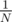 .
.
However you may notice this is the same as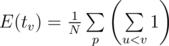 . For every vertex u, u will be visited before v:
. For every vertex u, u will be visited before v:
Then, we get to the equation mentioned.
thanks a lot. your explanation is great!
I too was stuck in the explanation mentioned in the tutorial ....really very beautifully explained
Very nice explanation! But why exactly u will be visited before v in N/2 of the permutation (in the third case)? Could you detail a little, please?
Look at a set of siblings, the array of direct children of some vertex. Then, after shuffling his array, there is nos reason for a vertex u to appear more than half of the permutations before v, as all permutations are equiprobable. That is, by symmetry, half of the permutations will have u < v and other half will have v < u.
You can extend this to the subtree of vertex u and v: a children x of vertex u will have 1 / 2 probability of happening before vertex v (think like it will inherit the probability from its parent) and also x will have 1 / 2 probability of happening after a vertex y that is a children of vertex v.
Thanks for your explanation. Not many people explain this way.
Really weak tests for D :(
Kostroma and zeliboba hacked my solution in several minutes after contest.
Correct answer (Arterm's solution)
Wrong answer (my solution)
Runtime exception (adamant's solution)
Could you add at least this test for upsolving if you don't mind?
My solution is ok. It's just stack overflow. Works in custom test.
Div2B question C:
Some algebra? Please help. Can't understand how to get the values of p and q.Use reduction to prove those formulas.
Here is a helpful link on solving recurrence relations.
Div1-C: What's the proof for the even/odd formula?
maybe my solution comments helps you : http://codeforces.com/contest/697/submission/19143565
numerator is a geometric sequence and you can find it's summation with formula
a*(p^n-1) / (p-1).if you simplify my formulas you will reach editorial formulas.
Express the dp[i]=(1 — dp[i-1])*0.5 in terms of fraction..then you can see that powers of 2 alternate in signs in numerator and denominator is 2^(n-1)...you can divide numerator in two halves....(2^0 + 2^2 + ...+2^(n-2)) — (2^1 + 2^3 + ... + 2^(n-3)) for evens and (2^1 + 2^3 + ...+2^(n-2)) — (2^0 + 2^2 + ..+ 2^(n-3)) for odds.. then you can use property of Geometric progression in numerator to get to the formula in the editorial
Thanks for the help! I found a more intuitive way (for me) to find the formulas.
When n is odd, the base case will be dp1 = 0 so we have a geometric progression 20, 22, 24, ... with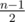 terms. So
terms. So 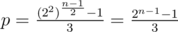 and q = 2n - 1.
and q = 2n - 1.
When n is even, the base case will be dp0 = 1 so in this case and q = 2n. After simplifying
and q = 2n. After simplifying  by 2 we get the formulas from the editorial.
by 2 we get the formulas from the editorial.
Could someone explain how the formula for Div 2D was derived in a more detailed way?
Check my comment above.
In 696F - ...Dary! I used the fact that there is some optimal placement with the two points on sides of the polygon. The editorial doesn't explain it, does it? Am I missing something? Can anybody prove it?
I got accepted with the following approach (19136466). For every of O(n2) intervals of sides I ternary search the optimal point (a point on one of sides, in order to minimize the maximum distance to lines in the fixed interval). There is no halfplanes intersection, only calculating the distance between a point and a line.
It's a pity that during the contest I had a bug in my ternary search. Though after the contest I didn't get AC at the first try anyway (precision).
After a contest I thought a bit more and realized many new things. For a fixed interval the distance to only the first line and the last line matters. So, for each interval it's enough to find a point on some side with equal distance to the first and the last line in the interval. It makes my solution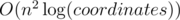 instead of
instead of 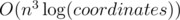 .
.
Furthermore, what I tried to ternary search is an angle bisector. It gives us O(n2) solution! Instead of coding it, I improved my first submission and now I find an agle bisector by binary search. Thanks to it, my code is short and it still doesn't use anything more complicated that the distance between line and point. The complexity is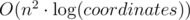 , my submission: 19140242.
, my submission: 19140242.
There is also one additional observation that helps.
If either i = j or the angle between vectors Pi Pi + 1 and Pj Pj + 1 is positive (as can be checked with cross product), call pair (i, j) good. The optimal solution can only be reached for intervals with both pairs (i, j) and (j + 1, i - 1) being good (with obvious interpretation modulo n). Now there are only O(n) candidate intervals to check.
What I did was checking for every interval if it can produce the optimal solution, and for every candidate interval I did a linear search for the segment intersected by the angle bisector on the interval. The total complexity is O(n2). It is also possible to improve this to by using two pointers to find the candidate intervals and binary searching the intersection segment, but O(n2) was reasonably fast and easier to code :P
by using two pointers to find the candidate intervals and binary searching the intersection segment, but O(n2) was reasonably fast and easier to code :P
During the contest I assumed that only good pairs (i, j) matter, as you described. It easily implies a proof that the two points should be on sides of the polygon and this is why my solution works. How to prove what you wrote?
Oh, you are right about O(n) candidates. I had this thought at some moment but I noticed that for fixed i there may be many j that both (i, j) and (j + 1, i - 1) are good. So I thought there are O(n2) candidates but yeah, it's easy to show that it's O(n) in total (because: two pointers).
EDIT. I implemented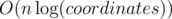 approach with two pointers (well, with three pointers). Submission: 19150097. Of course, it can be improved to O(n) by replacing binary search with some O(1) formulas.
approach with two pointers (well, with three pointers). Submission: 19150097. Of course, it can be improved to O(n) by replacing binary search with some O(1) formulas.
PrinceOfPersia, you invented an awesome problem.
My sketch of the proof is as follows:
For a minimal circle covering a non-good pair (i, j) (it has bigger radius than the circle covering [j + 1, i - 1]), we find a maximal good sub-pair (i', j') (meaning i' and j' lie on interval [i, j] mod n). Having a circle cover a smaller interval decreases the ray.
When considering the circle covering [j' + 1, i' - 1], we see that this is also formed by a good pair (otherwise we could either increase j' or decrease i').
As one of j' + 1 and i' - 1 necessarily belongs to the interval [i, j], we get immediately that the minimal ray of the circle covering [j' + 1, i' - 1] is smaller than that of a minimal circle covering [i, j].
From this, we see that any non-candidate interval is dominated by a candidate interval.
I second that this problem was very good, thank you PrinceOfPersia for this.
EDIT: Also, I don't think I understand how checking the intersection point of the polygon and angle bisector can be done in O(1), unless it is amortized? Even if we calculate the line bisecting the angle in constant time, don't we need to search for the side it intersects somehow?
Why does it have bigger radius?
How do we get it immediately? Sorry, I don't see it.
I use three pointers: start, whereMid and end. An interval is [start, end] and I binary search on side whereMid. Check my code for details.
Amazing!
I'm preparing a training for my classmates(we each collect some amazing problems and make up an exam),and I found this interesting problem. I have already implemented O(n3logn) (code) , O(n2logn) (code) , O(n2) (code) , O(nlogn) (code) and O(n) (code) ,they all have passed the data of this problem.
(Because my submissions can be seen as my classmates all follow me,I used my test account.)
But now there is a problem:I try to make a big convex(with n > = 20000 , random the points on a big circle) and change my array to map,the result is there is no pairs (i, j) that both (i, j) and (j + 1, i - 1) are calculated. And all of the O(n) submissions couldn’t pass the data . Your code couldn’t neither (but it can pass 696f)(code).
I don't know why and I believe that my data maker is correct(all the code can pass the data that n < = 1000).The data.
You passed the problem long time ago. Hope you can remember the solution and I’m looking forward to you reply. Thank you (And sorry for my poor English), I'm your big fan!
I can't download your input file. Can you upload it in some different website? Can be pastebin.
You should write a verificator program that will check if the input file is correct. Then let's think about the correctness of solutions.
Ubuntu Pastebin
Emm....I made a convex among the points and it's 20000 points on it as my expectation.
Sorry I couldn't reply you soon because there was 1 am seven hours ago.
And it was 1am for me seven hours ago, when you posted your comment ;p
Your input doesn't satisfy the problem constraints at all. N is too big and coordinates aren't integers.
Sorry I may ignored something: I want to change the problem constraints (so that the participants who use O(n) could get 100 points and who use O(n2logn) could get some points less than 100 , many important contests in China like give points in this way).
Now the problem is: I made bigger input and all of the codes (O(n)) couldn't pass the data. Of course I change
T best_r[][]into(unordered_)map<int,T> best_r[]andscanf("%d%d",&x,&y)intoscanf("%lf%lf",&x,&y).What you're talking about is called subtasks (subtasks for partial points) and is indeed common.
Either input is invalid or the O(n) solutions are incorrect. Try to find a small countertest and analyse it. And write an input verifier, as I told you.
I'm not surprised that my solution doesn't work because it was made for different constraints. You would have to go through it carefully to catch all places where something should be changed because of bigger N or non-integer coordinates.
Hi, I think solution to div1 D (div2 F) has a small typo. The dp calculation should be:
dp[l + 1][u] >= b[u] + dp[l][v] ?
In Div 1. D, I was not sure if matrix multiplication would work well if I change the definitions of
+and*. In particular, I was not sure if associativity of matrix multiplication stands true if I change those.Associativity means A·(B·C) = (A·B)·C
Can anyone help me proving this?
It can be done directly by writing what (i, j) cell of ABC equals to.
You can find a proof in this PDF.
Oh my, maths maths and maths, that's the moment when it has to feel bad to be a high school student... Can somebody tell me what should I search to learn about the proof behind the formula of Div2E? It looks similar to GS but it isn't it. =/
Edit: Whoops just found a link above in the comments, here in case if someone missed it too.
Whom I've hacked hacked me....
Scan in one line using scanf
For Div2B
what should be the output for 0.798e1 ?
07.98 or 7.98 ?
7.98 as it is mentioned in the question that Output doesn't contain leading zeroes.
Then the cases are weak . Because my code gets AC and i print 07.98 :P
From the task : Also, b can not be non-zero if a is zero. This test is not correct :)
Yes, look like that they haven't included such cases.
what is h[v] and depth[v] in div2D editorial?
I wrote down the complete before before arriving at ans of Div 2 'D' , if anyone wants to have a look u can message me
depth[v]=level of node v counted from root (root has level 1)
h[v]=depth[v]-1
n-sub[v]-h[v]=number of nodes that are neither in subtree of v nor an ancestor of v
In div1C , how can we solve the recurance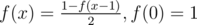 without using wolfram?
without using wolfram?
it can turn into the form: f(x) — k = -1/2*(f(x-1) — k), so f(x) — k is geometric sequence
Edit: I don't know why the minus sign becomes "&mdash" in codeforces
Can someone please tell me what is wrong with my solution to Div2 C? It got WA for test case 12.
I used the same idea as mentioned in the editorial. I just simulated the procedures (namely
updateandfindCost) using the concept of Lowest Common Ancestor(LCA).Thanks in advance.
#define pi pair<int,int>u and v are too large to store in an int, and your costs map's keys are pair<int,int>, so it overflows.
How to solve div2C ? I read editorial and saw some codes , but I really don't understand // If there hadn't been (so) infinite number of intersections it would have been much easier :D
For any pair of vertices, there will be a root(famously knows as Lowest common ancestor) such that you can reach one of the nodes by traversing left from root and reach other node by traversing right from root. Such traversal will give shortest path.
Let's make it more clear below.
For nodes 8 and 10, LCA is 2.
For nodes 9 and 3, LCA is 1.
For nodes 13 and 14, LCA is 3.
How to calculate LCA?
Parent of a node x is x/2. You can confirm this from above image.
parent[5]=2 parent[12]=6
Insert all parents of a node in a set. Then search for all parents of other node in this set. First node which you will find in the set will be LCA. Then you can easily traverse from each nodes to LCA and add value to each edge or calculate cost of path.
Code
In div2 D, I know depth[v] will added to our answer but I cannot understand how did we get first term? Can we solve it by calculating starting_time for each vertex and dividing by total number of paths possible(which maybe large)? For example in first testcase total number of paths are 12.
The first time is actually the delay term (the delay here means the starting time between a node and its parent).
Consider such a node u and its parent v, then for other nodes that is also having v as its parent, the total number of nodes of these nodes and their subtrees is actually n - sub[v] - h[v]. As each of them have 0.5 probability to contribute to the delay, the delay term would be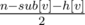 .
.
Why depth[v] is added can someone explain using linearity of expectation.
The depth is actually the time running from root to the target node u. That is, the expected value of all the delay with shift by this value, as no matter what is the search sequence, at least you have to go through the shortest path from the root to the node.
In Div2 C, I am getting WA at Test Case-39. Can't find any bug in the code.
Link -> Solution
Instead of log2(u) , use log2l(u) Here is the submission after modification: http://codeforces.com/contest/697/submission/19171319 Thank you
Thanks a lot! :)
For div2 D can anyone explain how to calculate the expected Value ?
Suppose the children of vertex v are c1, c2, ..ck.
Let note the probability pi, j, (i ≠ j) that in the permutation position of ci will be smaller than position of cj,then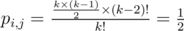 because you can fix position of ci,let it be t,then the position of cj must be greater that t,if t = 1 we have k - 1 ways,t = 2 we have k - 2 ways and so on,but
because you can fix position of ci,let it be t,then the position of cj must be greater that t,if t = 1 we have k - 1 ways,t = 2 we have k - 2 ways and so on,but 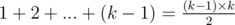 , and the remaining numbers we can add in (k - 2)! ways.
, and the remaining numbers we can add in (k - 2)! ways.
Let note S(ci) be the number of vertices in the subtree ci.
Now the answer for the cith vertex is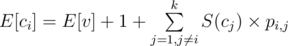 ,because E[x + y] = E[x] + E[y].
,because E[x + y] = E[x] + E[y].
Hi, can you please explain why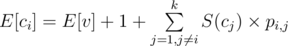 .
.
I can understand that E[ci] = E[v] + 1 but I could not understand the other part. Why are we taking the summation of number of vertices in subtree times the probability that Ci comes earlier than Cj. According to E[x] formula, shouldnt we do: E[c] = E[v] + 1 + (1/n!)*sigma(delay caused by i-th permutaion), where v is parent of c having n children.
Can anyone explain the matrix exponentiation approach for solving the recurrence for Div2E ?
Can someone explain Div 1 D in more detail?
Hello! Regarding Div 2 E, you need to compute 2^(n-1) % MOD. I know how to compute 2^n % MOD using binary exponentiation, but how do you get 2^(n-1) % MOD , as n may be huge?
Just compute x=2^n and then do x=x/2 using fermat's little theorem.
I made a nice explanation for Div2 D / Div1 B
Here
If anybody needs in more detailed solution of problem 'Div1 C. Please'. You can read it here by looking at my post.
Actually, for div2 E there's another solution without even using dp. If you come up with the transition matrix, namely:
Then you can simply use the exponential power with the following formula:
, where
phi(x)is the Euler function.22299208
In problem Div-1 C ,
Let, x = 2^(n-1) — 1,
and y = 2^(n-1) + 1;
How can you ensure x , y are always divisible by 3 ?
Is it really necessary ? If x is not divisible by 3 , then wouldn't (x/3) be a non-integer ?
I'm a bit confused
Oh...the monster is so scary!!!!
I have to F12....